《机械工程控制基础》课程教学资源（PPT课件）第三章 系统的时域分析

第三章系统的时域分析 数学模型 性能分析：稳、快、准等 时域分析法 直观 根轨迹法 频率法 微分方程 L和L 时间响应 表达式 曲线 性能分析

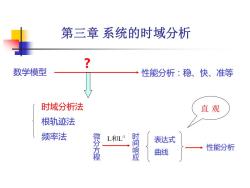
数学模型 性能分析：稳、快、准等 ? 时域分析法 根轨迹法 频率法 微 分 方 程 -1 L L 和 时 间 响 应 表达式 曲线 性能分析 第三章 系统的时域分析 直 观

本章内容 一.系统的时间响应及其组成 (一) 二典型的输入信号 三，对一阶、二阶、高阶系统的典型时间响应进行分析 四.分析性能指标（时域) (二)五.系统误差分析与计算

本章内容 （一） 一. 系统的时间响应及其组成 二. 典型的输入信号 三. 对一阶、二阶、高阶系统的典型时间响应进行分析 四. 分析性能指标（时域） （二） 五. 系统误差分析与计算

§3-1时域响应及典型输入信号 一时域响应 在输入信号的作用下，其输出随时间的变化过程x(t) (t)=L'(s)=LG(s).X,(s) 1.瞬态响应和稳态响应： 输入引起的时间响应由瞬态和稳态两部分组成

§3-1 时域响应及典型输入信号 0 x t( ) 一.时域响应 在输入信号的作用下，其输出随时间的变化过程 。 ( )  ( )  ( ) ( ) 1 1 x t L X s L G s X s o O i = = • − − 1. 瞬态响应和稳态响应： 输入引起的时间响应由瞬态和稳态两部分组成

§3-1时间响应的典型输入信号 例： y(t) mi+cy+ky=F sinot Fsinwt 令,=k,5= F m m 2mk y+260.y+0y-Fsinol m ky Fsinwt, m 非齐次常微分方程的完全解： .y(t)=Ae 5o sin(-21+0)+Bsin(ot+) 自由衰减震荡 受迫振动 瞬态响应 稳态响应

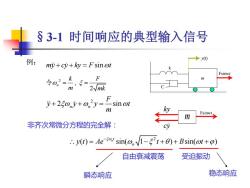
§3-1 时间响应的典型输入信号 my cy ky F t + + = sin 自由衰减震荡 受迫振动 2 , 2 n k F m mk 令  = = 2 2 sin n n F y y y t m + + =    2 ( ) sin( 1 ) sin( ) n t n y t Ae t B t       −  = − + + + 例： m Fsinwt C k y(t) 非齐次常微分方程的完全解： 瞬态响应 稳态响应 m ky Fsinwt cy

§3-1时域响应及典型输入信号 瞬态响应系统在某一输入信号的作用下，其输出量从初始状态 稳定状态的响应过程。（过渡过程) 稳态响应当某一信号输入时，系统在时间趋于无穷大时的输出 状态。（静态） 2.系统的时域响应分析 在时间域内，研究各种形式的输入信号作用下，系统输出响应的时间 特征，即对系统施加一定形式的输入信号，然后研究系统的输出量随时 间的变化规律

瞬态响应 系统在某一输入信号的作用下，其输出量从初始状态 稳定状态的响应过程。（过渡过程） 稳态响应 当某一信号输入时，系统在时间趋于无穷大时的输出 状态。（静态） 2. 系统的时域响应分析 在时间域内，研究各种形式的输入信号作用下，系统输出响应的时间 特征，即对系统施加一定形式的输入信号，然后研究系统的输出量随时 间的变化规律。 §3-1 时域响应及典型输入信号

二、典型的输入信号 1.阶跃函数 a, t>0 X x,(t)= 0, t<0 a=1时，单位阶跃函数 2.斜坡函数 at,t0 x,(t)= 0,t<0 a=1时，单位斜坡函数

1.阶跃函数 2.斜坡函数 0 ( ) 0, 0 i at t x t t   =    ， 二、典型的输入信号 , 0 ( ) 0, 0 i a t x t t   =    a =1 时，单位阶跃函数 xi t a a =1 时，单位斜坡函数 xi t

二、典型的输入信号 3.加速度函数 t>0 x()= at2, 0, t0 x()= 0, t<0

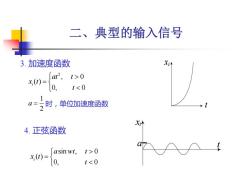
二、典型的输入信号 2 , 0 ( ) 0, 0 i at t x t t   =    xi t 3. 加速度函数 时，单位加速度函数 1 2 a = sin , 0 ( ) 0, 0 i a wt t x t t   =    4. 正弦函数 xi a t

二、典型的输入信号 5.脉冲函数 Xi a/to lim 0o a=1时，单位脉冲函数 to .Xo(s)=X,(s).G(s) 当X,()=6t)→X,(s)=1 ∴.Gs)=Xos)=xt] x.() 脉冲响应函数 系统传递函数即为脉冲响应函数的象函数

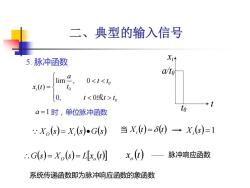
二、典型的输入信号 X (s) X (s) G(s) O i  = • X (t) (t) i =  Xi (s) =1 G(s) X (s) Lx (t)  = O = o x (t) o 脉冲响应函数 当 0 0 lim , 0 ( ) 0, 0 0 i a t t x t t t t t     =      或 xi t t0 a/t0 5. 脉冲函数 a =1 时，单位脉冲函数 系统传递函数即为脉冲响应函数的象函数

二、典型的输入信号 输入信号的选择应视不同系统的具体工作状况而定： 1)若输入量是随时间逐渐变化的函数，如机床、雷达天线、 火炮等，一→选斜坡函数 2)若输入量是冲击量，如导弹发射等，一选脉冲函数 3)若输入量随时间往复运动，如机床振动，一选正弦函数 4)若输入量是突然变化的，如断电、合电等，一选阶跃函数

二、典型的输入信号 输入信号的选择应视不同系统的具体工作状况而定： 1）若输入量是随时间逐渐变化的函数，如机床、雷达天线、 火炮等， 2）若输入量是冲击量，如导弹发射等， 3）若输入量随时间往复运动，如机床振动， 4）若输入量是突然变化的，如断电、合电等， 选斜坡函数 选脉冲函数 选正弦函数 选阶跃函数

§3.2一阶系统的时域响应 一阶系统：能够用一阶微分方程描述的系统。 典型形式：一阶惯性环节 Xo(s) 1 X(s) Ts+1 一、一阶系统的单位阶跃响应 G-[x() x(0)=1→X,(s)= X(s)= 1,1▣☑-11 Ts+1 ss Ts+1 s 1 →x(t)=1-e7 S+

§3.2 一阶系统的时域响应 一阶系统：能够用一阶微分方程描述的系统。 典型形式：一阶惯性环节 一、一阶系统的单位阶跃响应 0 ( ) 1 ( ) 1 i X s X s Ts = + ( ) 1 i x t = 1 ( ) X s i s = 0 1 1 1 ( ) 1 1 T X s Ts s s Ts =  = − + + 0 ( ) 1 t T x t e − = − 1 1 s 1 s T = − + 1 ( ) 0 0 1 1 1 S S C X S s Ts = = =  = =     + ( ) 1 2 1 1 ( 1) S T S T C X S Ts T s = − = − =  + = = −    