《机械工程控制基础》课程授课教案（讲义）第六章 控制系统的性能分析与校正

第六章控制系统的性能分析与校正 对于一个控制系统来说，其基本性能要求是稳定、准确、快速，其他 的要求还有经济性、工艺性、体积、寿命等。在分析和设计系统时，需 要具备一定的实践经验。 本章只从控制系统的角度，讨论控制系统的系统综合和校正问题。 如果一个系统的元部件及参数已经给定，就要分析它能达到什么指标， 能否满足所要求的各项性能指标，这就是性能分析问题。 若系统不能全面地满足所要求的性能指标，则可考虑对原已选定的系 统增加必要的元件或环节，使系统能够全面地满足所要求的性能指标， 这就是系统的综合与校正。 内容： 1、简单介绍系统的时域性能指标和频域性能指标。 2、重点介绍利用频域法如何分析和综合一个系统，介绍几种校 正的作用。 本章内容： 「（一）、系统的性能指标，校正的一般概念，常用的校正方法与分类： (二)、相位超前校正，相位滞后校正，相位超前-滞后校正的基本特性 及其频域设计方法； (三)、PID调节器的基本特性与设计方法： 、(四)、顺馈校正与反馈校正的基本特性

第六章 控制系统的性能分析与校正 对于一个控制系统来说，其基本性能要求是稳定、准确、快速，其他 的要求还有经济性、工艺性、体积、寿命等。在分析和设计系统时，需 要具备一定的实践经验。 本章只从控制系统的角度，讨论控制系统的系统综合和校正问题。 如果一个系统的元部件及参数已经给定，就要分析它能达到什么指标， 能否满足所要求的各项性能指标，这就是性能分析问题。 若系统不能全面地满足所要求的性能指标，则可考虑对原已选定的系 统增加必要的元件或环节，使系统能够全面地满足所要求的性能指标， 这就是系统的综合与校正。 内容： 1、简单介绍系统的时域性能指标和频域性能指标。 2、重点介绍利用频域法如何分析和综合一个系统，介绍几种校 正的作用。 本章内容： （一）、系统的性能指标，校正的一般概念，常用的校正方法与分类； （二）、相位超前校正，相位滞后校正，相位超前-滞后校正的基本特性 及其频域设计方法； （三）、PID 调节器的基本特性与设计方法； （四）、顺馈校正与反馈校正的基本特性

§6.1系统的性能指标 设计某个控制系统的目的，是用来完成某一特定的任务。控制系统 可分为被控对象和控制装置两大部分，当被控对象确定后，则可对控制 系统提出要求，通常以性能指标来表示，这些指标常常与精度、相对稳 定性和响应速度有关。 系统的性能指标，按其类型可分为： (1)时域性能指标：包括瞬态和稳定性能指标： (2)频域性能指标：它不仅反映系统在频域方面的特性，而且当时域 性能不易求得，可首先用频率特性实验来求得该系统在频域中的动态性 能，再由此推出时域中的动态性能。 (3)综合性能指标：它是考虑对系统的某些重要参数应如何取值才能 保证系统获得某一最优的综合性能的测度。即：若对这个性能指标取极 值，则可获得有关重要参数值，而这些参数值可保证这一综合性能为最 优。 一、时域性能指标： 评价控制系统优劣的性能指标，一般是根据系统在典型输入下输出 响应的某些特点统一规定的。 例.单位阶跃下二阶欠阻尼系统的时域指标：

§6.1 系统的性能指标 设计某个控制系统的目的，是用来完成某一特定的任务。控制系统 可分为被控对象和控制装置两大部分，当被控对象确定后，则可对控制 系统提出要求，通常以性能指标来表示，这些指标常常与精度、相对稳 定性和响应速度有关。 系统的性能指标，按其类型可分为： ⑴时域性能指标：包括瞬态和稳定性能指标； ⑵频域性能指标：它不仅反映系统在频域方面的特性，而且当时域 性能不易求得，可首先用频率特性实验来求得该系统在频域中的动态性 能，再由此推出时域中的动态性能。 ⑶综合性能指标：它是考虑对系统的某些重要参数应如何取值才能 保证系统获得某一最优的综合性能的测度。即：若对这个性能指标取极 值，则可获得有关重要参数值，而这些参数值可保证这一综合性能为最 优。 一、时域性能指标： 评价控制系统优劣的性能指标，一般是根据系统在典型输入下输出 响应的某些特点统一规定的。 例.单位阶跃下二阶欠阻尼系统的时域指标：

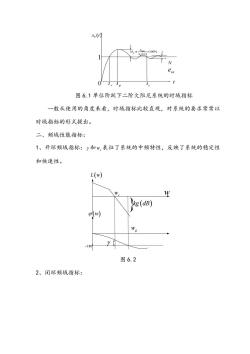
x.(rI 图6.1单位阶跃下二阶欠阻尼系统的时域指标 一般从使用的角度来看，时域指标比较直观，对系统的要求常常以 时域指标的形式提出。 二、频域性能指标： 1、开环频域指标：y和，表征了系统的中频特性，反映了系统的稳定性 和快速性。 L(w) g(dB) (w) -180叶 图6.2 2、闭环频域指标：

01 x t 0   t r t p t s t   max 0 p 100% x M x     N ss e 图 6.1 单位阶跃下二阶欠阻尼系统的时域指标 一般从使用的角度来看，时域指标比较直观，对系统的要求常常以 时域指标的形式提出。 二、频域性能指标： 1、开环频域指标：  和 wc 表征了系统的中频特性，反映了系统的稳定性 和快速性。 0  180   w L w  wc wg kg dB   w 图 6.2 2、闭环频域指标：

A ANO△ 1.707A(0 1/ 图6.3 谐振峰位：从=希 w。→复现频率 0~w:复现低频正弦输入信号的带宽（工作带宽）。 。→闭环截止频率，从A0)下降3B时的w。 0~W:闭环带宽。 在基于频域特性的设计中，常将时域指标转换成频域指标来考虑。 频城性能指标与时城性能指标间有一定的关系，例如，？、，与 ,有关，当阻尼比5一定时，截止频率，与，、马都呈反比关系，即：带 宽越↑，系统响应输入信号的快速性个。 例：1：G间动 T=1,w1=1=1w1 1:G.(-35 1 T=3n=月wg

Amax A0  0.707A 0   wM wr wb w 图 6.3 谐振峰值： max (0) r A M A  wm 复现频率 0~ wm ：复现低频正弦输入信号的带宽（工作带宽）。 wb 闭环截止频率，从 A(0) 下降 3dB 时的 w。 0~ wb ：闭环带宽。 在基于频域特性的设计中，常将时域指标转换成频域指标来考虑。 频域性能指标与时域性能指标间有一定的关系，例如， g e 、 p t 、 s t 与 wb 有关，当阻尼比  一定时，截止频率 wb 与 p t 、 s t 都呈反比关系，即：带 宽越  ，系统响应输入信号的快速性  。 例：I： 1   1 1 G s s   T 1, 1 1 1 w w T b   II： 2   1 3 1 G s s   T  3, 2 2 1 3 w w T b  

L(w) 0.1 W 1/3N 3dB 图6.4W1>w2,所以，1的响应速度个，有较好的跟随性能。 xo(1) x 图6,5单位阶跃响应齐，1〢的惯性 xof(t) x,(t) 图6.6单位斜坡响应 三、综合性能指标（误差准则） 目前使用的综合性能指标有许多种，简单介绍如下： 1、误差积分性能指标。 对于一个理想的系统，若输入为阶跃，输出也应为阶跃。实际上， 输入与输出间总存在误差，我们只能使误差()尽可能↓

0.1L w  wb2 wb1 1/ 3 3dBI I I w 图 6.4 w w b b 1 2  ，所以，I 的响应速度  ，有较好的跟随性能。 I I I x t i   x t 0   01 T t 图 6.5 单位阶跃响应 1 k T   ，II 的惯性  I I I x t i   x t 0   t 图 6.6 单位斜坡响应 三、综合性能指标（误差准则） 目前使用的综合性能指标有许多种，简单介绍如下： 1、误差积分性能指标。 对于一个理想的系统，若输入为阶跃，输出也应为阶跃。实际上， 输入与输出间总存在误差，我们只能使误差 e t  尽可能 

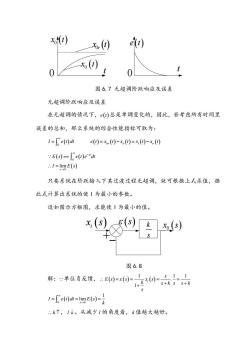
xo(t) t) x() 04 0 图6.7无超调阶跃响应及误差 无超调阶跃响应及误差 在无超调的情况下，()总是单调变化的，因此，若考虑所有时间里 误差的总和，那么系统的综合性能指标可取为： 1=0dhe0=x()-x0=x0-x0 :E(s)=[e(t)e-"dt :.I=limE(s) 只要系统在阶跃输入下其过渡过程无超调，就可根据上式求值，据 此式计算出系统的使丨为最小的参数。 设如图示方框图，求能使1为最小的值。 x(s)(5)) 图6.8 解单我反线。0-0甘动 1=e0h=g)-是 k↑，1↓。从减少1的角度看，k值越大越好

x t 0r   x t 0   t x t 0   0 0 t e t  图 6.7 无超调阶跃响应及误差 无超调阶跃响应及误差 在无超调的情况下， e t  总是单调变化的，因此，若考虑所有时间里 误差的总和，那么系统的综合性能指标可取为：   0 I e t dt    e t x t x t x t x t       or o i o               0 0 lim st s E s e t e dt I E s        只要系统在阶跃输入下其过渡过程无超调，就可根据上式求值，据 此式计算出系统的使 I 为最小的参数。 设如图示方框图，求能使 I 为最小的值。 k s x s i    s x s 0     图 6.8 解： 单位负反馈，       1 1 1 . 1 i s E s s x s k s k s s k s             0 0 1 lim s I e t dt E s k        k ，I 。从减少 I 的角度看， k 值越大越好

当系统的过渡过程有超调时，由于误差有正有负，积分后不能反映 整个过程误差的大小，所以若不能预先知道系统的过渡过程有无超调 就不能应用上式计算〡值，以评价所有时间里面误差总和的大小。 2、误差平方积分性能指标： 若给系统以单位阶跃输入后，其输出过渡过程有振荡时，则常取误 差平方的积分为系统的综合性能指标，即1=∫e()d。 由于积分号中为平方项，所以()的正负不会互相抵消，积分上限可 由足够大的时间T来代替，性能最优系统就是上式积分取极小的系统。 因为用分析和实验的方法来计算上式右边的积分比较容易，所以在 实际应用时，往往采用这种性能指标来评价系统性能的优劣，这也是现 代控制理论中的二次型性能指标的一种。 xt) 0 0 (b) 0 c d 图6.9(4个)阶跃响应及误差、误差平方、误差平方积分曲线 误差平方积分性能指标的特点是： 重视大的误差，忽略小的误差。因为误差大时，其平方更大，对〡的

当系统的过渡过程有超调时，由于误差有正有负，积分后不能反映 整个过程误差的大小，所以若不能预先知道系统的过渡过程有无超调， 就不能应用上式计算 I 值，以评价所有时间里面误差总和的大小。 2、误差平方积分性能指标： 若给系统以单位阶跃输入后，其输出过渡过程有振荡时，则常取误 差平方的积分为系统的综合性能指标，即   2 0 I e t dt    。 由于积分号中为平方项，所以 e t  的正负不会互相抵消，积分上限可 由足够大的时间 T 来代替，性能最优系统就是上式积分取极小的系统。 因为用分析和实验的方法来计算上式右边的积分比较容易，所以在 实际应用时，往往采用这种性能指标来评价系统性能的优劣，这也是现 代控制理论中的二次型性能指标的一种。 x t 0r   x t 0   t 0 0 t e t  1 0 t   2 e t 0 t   2 e t dt  a b c d  图 6.9（4 个）阶跃响应及误差、误差平方、误差平方积分曲线 误差平方积分性能指标的特点是： 重视大的误差，忽略小的误差。因为误差大时，其平方更大，对 I 的

影响大，所以根据这种指标设计的系统，能使大的误差迅速减小，但系 统易产生振荡 3、广义误差平方积分性能指标 取：1=e)+ae回u α→给定的加权系数 所以最优系统就是使此性能指标/取极小的系统 此指标的特点是既不允许大的动态误差)长期存在，又不允许大的 误差变化率e()长期存在。 所以按此准则设计的系统，不仅过渡过程结束得快，且过渡过程的变 化也较平稳

影响大，所以根据这种指标设计的系统，能使大的误差迅速减小，但系 统易产生振荡。 3、广义误差平方积分性能指标 取:     ' 2 2 0 I e t e t dt              给定的加权系数 所以最优系统就是使此性能指标 I 取极小的系统 此指标的特点是既不允许大的动态误差 e t  长期存在，又不允许大的 误差变化率   ' e t 长期存在。 所以按此准则设计的系统，不仅过渡过程结束得快，且过渡过程的变 化也较平稳

§6.2系统的校正 性能指标通常是由控制系统的用户提出。一个具体系统对指标的要 求应有所侧重，如调速系统对平稳性和稳态精度要求严格，而随动系统 对快速性期望很高。 性能指标的提出要有根据，不能脱离实际的可能性，比如要求响应快， 则必须有足够好的能量供给系统和能量转化系统，以保证运动部件具有 较好的加速度，运动部件要能承受产生的离心载荷和惯性载荷等。性能 指标决定于系统的设计水平和工艺水平。此外，由于它的性能指标常需 要昂贵的元件，因此成本高。 另一方面，几个性能指标的要求也经常互相矛盾。例如，减小系统的 稳态误差往往会降低系统的相对稳定性，甚至导致系统不稳定。在这种 情况下，就要考虑哪个性能时主要的，首先加以满足：有时，在另一些 情况下就要采取折中的方案，并加上必要的校正，使两方面的性能都能 得到部分满足。 一、校正的概念： 所谓校正（或称补偿调节），就是指在系统中增加新的环节，以改善系 统的性能的方法。 -1.d b

§6.2 系统的校正 性能指标通常是由控制系统的用户提出。一个具体系统对指标的要 求应有所侧重，如调速系统对平稳性和稳态精度要求严格，而随动系统 对快速性期望很高。 性能指标的提出要有根据，不能脱离实际的可能性，比如要求响应快， 则必须有足够好的能量供给系统和能量转化系统，以保证运动部件具有 较好的加速度，运动部件要能承受产生的离心载荷和惯性载荷等。性能 指标决定于系统的设计水平和工艺水平。此外，由于它的性能指标常需 要昂贵的元件，因此成本高。 另一方面，几个性能指标的要求也经常互相矛盾。例如，减小系统的 稳态误差往往会降低系统的相对稳定性，甚至导致系统不稳定。在这种 情况下，就要考虑哪个性能时主要的，首先加以满足；有时，在另一些 情况下就要采取折中的方案，并加上必要的校正，使两方面的性能都能 得到部分满足。 一、校正的概念： 所谓校正（或称补偿调节），就是指在系统中增加新的环节，以改善系 统的性能的方法。 m I R e ① ② ③   2 1, jo 0 1   ' k jo ,   0 k jo ,  ① w1 w w2 w  0  1 1, jo  a b

例：如图6.10.a k G.)F+Ts0+7s0+T网 (p=0) 为图中①，包围点(-1，j),所以系统不稳定 改进：「①k↓→k→图中②，稳定，但.↑，不希望甚至不允许 (②增加新环节，图中③w→w,发生变化，稳定 不改变k,不增大e.。 图6.10.b (p=0),稳定，但相位裕度y↓ 改进：①k↓，y无变化，无改善。 ②加入新环节，使曲线→②，%→w,间产生正的相移，y↑，得 到改善。 由上可知：从频率法德观点来看，增加新的环节，主要是改变系统的 频率特性。对系统品质指标的要求，最终可归结为对系统开环频率特性 的要求。系统设计的实质就是利用校正装置对系统开环Bode图进行整形。 要求它①在低频区(ww),表征系统的复杂性及噪声抑制性能，高频 增益应尽可能小，开环幅频特性尽可能快的衰减，以减少高频 噪声对系统的千扰。若原有高频段已符合要求，则校正时可保

例：如图 6.10.a   1 1 1 1 2 3    k k G s T s T s T s      p  0 为图中①，包围点 1, jo ，所以系统不稳定 改进：① k k   图中②，稳定，但 ss e ，不希望甚至不允许 ②增加新环节，图中③ w w 1 2  发生变化，稳定 不改变 k ，不增大 ss e 。 图 6.10.b  p  0 ，稳定，但相位裕度   改进：① k ， 无变化，无改善。 ②加入新环节，使曲线  ②， w w 1 2  间产生正的相移， ，得 到改善。 由上可知：从频率法德观点来看，增加新的环节，主要是改变系统的 频率特性。对系统品质指标的要求，最终可归结为对系统开环频率特性 的要求。系统设计的实质就是利用校正装置对系统开环 Bode 图进行整形。 要求它①在低频区（ w w c ），提供尽可能高的增益， ss e ，达到以最小 的误差跟踪输入； ②在中频区（ w w c 附近），表征闭环系统的动态性能，限制幅 频特性曲线， k dB dec  20 / 左右，以保证系统的稳定性（ r 和 g k ）， 使系统具有良好的动态性能。 ③在高频区（ w w c ），表征系统的复杂性及噪声抑制性能，高频 增益应尽可能小，开环幅频特性尽可能快的衰减，以减少高频 噪声对系统的干扰。若原有高频段已符合要求，则校正时可保