《机械工程控制基础》课程授课教案（讲义）第三章 系统的时域分析

第三章系统的时域分析 数学模型→性能分析：稳、快、准等 时域分祈法 根轨迹法 频率法 、直观 微分方程+时间响应表达式 曲线 >性能分析 本章内容 系统的时间响应及其组成 (一) 典型的输入信号 三.对一阶、二阶、高阶系统的典型时间响应进行分析 四.分析性能指标（时域） (二)五.系统误差分析与计算

第三章 系统的时域分析 数学模型 性能分析：稳、快、准等 时域分析法 根轨迹法 频率法 微分方程 时间响应 表达式 曲线 性能分析 本章内容 一. 系统的时间响应及其组成 （一） 二. 典型的输入信号 三. 对一阶、二阶、高阶系统的典型时间响应进行分析 四. 分析性能指标（时域） （二） 五. 系统误差分析与计算 直 观

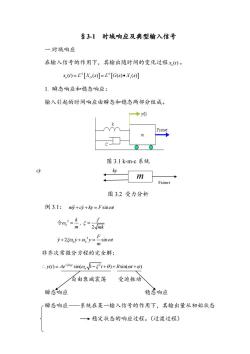
§3-1时域响应及典型输入信号 一时域响应 在输入信号的作用下，其输出随时间的变化过程x,①。 x(t)=L'[Xo(s)]=L'[G(s).x(s)] 1.瞬态响应和稳态响应： 输入引起的时间响应由瞬态和稳态两部分组成。 →y0 00 图3.1k-m-c系统 图3.2受力分析 例3.1：m+c少+y=Fsinot 细-点 f 2y-Fsinot 非齐次常微分方程的完全解： ∴J0=Aesin(o,V1-5i+0)+Bsin(or+p）) 有由衰减震荡受迫振动 瞬态响应 稳态响应 瞬态响应一系统在某一输入信号的作用下，其输出量从初始状态 →稳定状态的响应过程。（过渡过程)

§3-1 时域响应及典型输入信号 一.时域响应 在输入信号的作用下，其输出随时间的变化过程 () o x t 。     1 1 ( ) ( ) ( ) ( ) o O i x t L X s L G s X s      1. 瞬态响应和稳态响应： 输入引起的时间响应由瞬态和稳态两部分组成。 图 3.1 k-m-c 系统 m Fsinwt 图 3.2 受力分析 例 3.1： my cy ky F t    sin 2 , 2 n k f m mk 令    2 2 sin n n F y y y t m       非齐次常微分方程的完全解： 2 ( ) sin( 1 ) sin( ) n t n y t Ae t B t              自由衰减震荡 受迫振动 瞬态响应 稳态响应 瞬态响应 系统在某一输入信号的作用下，其输出量从初始状态 稳定状态的响应过程。（过渡过程） cy ky

稳态响应一当某一信号输入时，系统在时间趋于无穷大时的输出 状态。（静态） 2.系统的时域响应分析 在时间域内，研究各种形式的输入信号作用下，系统输出响应的时 间特征，即对系统施加一定形式的输入信号，然后研究系统的输出量随 时间的变化规律。 二、典型的输入信号 1.阶跃函数（图3.3) 0=6e0 a=1时，单位阶跃函数 图3.3阶跃函数 图3.4斜坡函数 2.斜坡函数（图3.4） 0=任8 a=1时，单位斜坡函数 3.加速度函数（图3.5) 1<0 a=)时，单位加速度函数 a/to +1 图3.5加速度函数 图3.6脉冲函数

稳态响应 当某一信号输入时，系统在时间趋于无穷大时的输出 状态。（静态） 2. 系统的时域响应分析 在时间域内，研究各种形式的输入信号作用下，系统输出响应的时 间特征，即对系统施加一定形式的输入信号，然后研究系统的输出量随 时间的变化规律。 二、典型的输入信号 1.阶跃函数（图 3.3） , 0 ( ) 0, 0 i a t x t t       a 1 时，单位阶跃函数 xi t a xi t 图 3.3 阶跃函数 图 3.4 斜坡函数 2.斜坡函数（图 3.4） 0 ( ) 0, 0 i at t x t t       ， a 1 时，单位斜坡函数 3. 加速度函数（图 3.5） 2 , 0 ( ) 0, 0 i at t x t t       1 2 a  时，单位加速度函数 xi t xi t t0 a/t0 图 3.5 加速度函数 图 3.6 脉冲函数

4.脉冲函数（图3.6） lima,06 5.正弦函数（图3.7) 40-8 X(s)=X(s)G(s)当X()=6()→0 :G(s)=X(S)=[x(]x)—脉冲响应函数 A! 图3.7正弦函数 输入信号的选择应视不同系统的具体工作状况而定： 1)若输入量是随时间逐渐变化的函数，如机床、雷达天线、火炮等， →选斜坡函数 2)若输入量是冲击量，如导弹发射等，→选脉冲函数 3)若输入量随时间往复运动，如机床振动，→选正弦函数 4)若输入量是突然变化的，如断电、合电等，→选阶跃函数

4. 脉冲函数（图 3.6） 0 0 lim , 0 ( ) 0, 0 0 i a t t x t t t t t           或 a 1 时，单位脉冲函数 5. 正弦函数（图 3.7） sin , 0 ( ) 0, 0 i a wt t x t t       X s X s G s O i         当 X t t i       r    G s X s L x t   O o         x t o   脉冲响应函数 图 3.7 正弦函数 输入信号的选择应视不同系统的具体工作状况而定： 1）若输入量是随时间逐渐变化的函数，如机床、雷达天线、火炮等， 选斜坡函数 2）若输入量是冲击量，如导弹发射等， 选脉冲函数 3）若输入量随时间往复运动，如机床振动， 选正弦函数 4）若输入量是突然变化的，如断电、合电等， 选阶跃函数

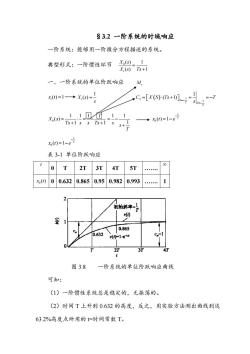
§3.2一阶系统的时域响应 一阶系统：能够用一阶微分方程描述的系统。 典型形式：一阶惯性环节1 X,(s)Ts+1 一、一阶系统的单位阶跃响应M 11回11 X,)=5+1店+15s+7 +0=1-e7 x)=1-e7 表3-1单位阶跃响应 0T2T 3T 4T5T . x000.6320.8650.950.9820.993. 1 2 初始斜率= 1.865 图3.8一阶系统的单位阶跃响应曲线 可知： (1)一阶惯性系统总是稳定的，无振荡的。 (2)时间T上升到0.632的高度，反之，用实验方法测出曲线到达 63.2%高度点所用的=时间常数T

§3.2 一阶系统的时域响应 一阶系统：能够用一阶微分方程描述的系统。 典型形式：一阶惯性环节 0 ( ) 1 ( ) 1 i X s X s Ts   一、一阶系统的单位阶跃响应 M r ( ) 1 i x t  1 ( ) X s i s    1 2 1 1 ( 1) S T S T C X S Ts T s               0 1 1 1 ( ) 1 1 T X s Ts s s Ts       1 1 s 1 s T    0 ( ) 1 t T x t e    0 ( ) 1 t T x t e    表 3-1 单位阶跃响应 t 0 T 2T 3T 4T 5T .  0 x t() 0 0.632 0.865 0.95 0.982 0.993 . 1 图 3.8 一阶系统的单位阶跃响应曲线 可知： （1）一阶惯性系统总是稳定的，无振荡的。 （2）时间 T 上升到 0.632 的高度，反之，用实验方法测出曲线到达 63.2%高度点所用的 t=时间常数 T

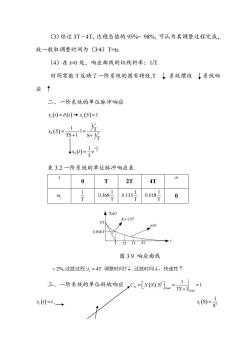
(3)经过3T-4T,达稳态值的95%98%，可认为其调整过程完成， 故一般取调整时间为(34)Ts (4)在0处，响应曲线的切线斜率：1/T 时间常数T反映了一阶系统的固有特性，T↓系统惯性↓系统响 应↑ 二、一阶系统的单位脉冲响应 x(0)=8()+x(S)=1 =1安 k0 表32一阶系统的单位脉冲响应表 t 0 T 2T 4T 0368013500181 0 4X) 你 0.368/T- 十27T行 图3.9响应曲线 <2%,过渡过程：，=4T调整时间T↓，过渡时间↓，快速性个 三、一阶系统的单位斜放响应-[Xs1 x()=1,→ x(5)-

（3）经过 3T 4T，达稳态值的 95% 98%，可认为其调整过程完成， 故一般取调整时间为（3 4）T=ts. （4）在 t=0 处，响应曲线的切线斜率：1/T. 时间常数 T 反映了一阶系统的固有特性,T , 系统惯性 , 系统响 应 二、一阶系统的单位脉冲响应 x t t i         1 i x S  0   1 1 T 1 TS 1 S+ 1 T x S       T 0 1 T t x t e   表 3.2 一阶系统的单位脉冲响应表 t 0 T 2T 4T  r 1 T 1 0.368 T 1 0.135 T 1 0.018 T 0 X0(t) t 1/T 0.368/T T 2T 3T 4T K=-1/T2 w(t) 图 3.9 响应曲线 2%, 4T s      过渡过程;t 调整时间T ,过渡时间 ，快速性 三、一阶系统的单位斜坡响应   2 11 0 0 1 S 1 1 S S C X S TS              , i x t t    2 1 S S i x 

←2s到现{lL 6日哥里风 T M.=A. C.-[ 1=0,x(=0,e(o)=x(o)-x(o)=T ◆X(0 1/T X()个e(em=T 0.368/T Xo(t)=t-T+TeVr 图3.10响应曲线 瞬态响应的特性反应系统本身的特性，叶响应速度↓。 输入试验信号是为了识别系统的特性，系统特性取决于系统的参数， 不取决于外作用的形式。 例3.2两个T值不同的惯性环节串联，求其单位阶跃响应，已知 G(S)=(S) 11 xS105+1S+7 。11 111_-0.09」 解：xS)-10sS中1s0s+s*1*s 9.1 x0-=0ei+g1

      2 12 2 0 0 0 1 S S 1 S 1 S d d T C X S T ds ds TS   TS                         2 0 2 2 2 1 1 1 T T 1 T T S TS+1 S S S TS+1 S S S+1/T x         M A r  max   2 2 1/ 2 1/ 1 ( s+1) S T S T C X S T T S             t , x t 0    , e x x T ( )       i   0   X0(t) t 1/T 0.368/T e(∞)=T X0(t)=t-T+Te -t/T Xi(t)=t 图 3.10 响应曲线 瞬态响应的特性反应系统本身的特性，T 响应速度 。 输入试验信号是为了识别系统的特性，系统特性取决于系统的参数， 不取决于外作用的形式。 例 3.2 两个 T 值不同的惯性环节串联，求其单位阶跃响应，已知     0 1 1 G(S) 10 1 1 i x S x S S S     = 。 解： x S 0    1 1 1 1 1 1 0.09 9 10 1 1 S 10 1 1 S S S S S           1 L    10 0 1 1 1 0.09 9 t t x t e e      

+Xo(0 w↑S] 2 S2 S1 +0 图3.11响应曲线示意图 图3.12极值分布图 系统响应取决于T,T值小，对响应影响小。 靠近虚轴的极点起主导作用

X0(t) t 3 2 1 jw × × σ s2 s1 [S] 图 3.11 响应曲线示意图 图 3.12 极值分布图 系统响应取决于 T，T 值小，对响应影响小。 靠近虚轴的极点起主导作用

§3.3二阶系统的时域响应 二阶系统：由二阶微分方程描述的系统。 许多高阶系统常近似为二阶系统来研究，所以具有重要意义。 一典型的二阶系统的数学模型 G9=⑨ x(S)S2+250S+m 5:阻尼比0：无阻尼固有频率 令上式分母=0，得二阶系统的特征方程： S2+250S+0,2=0 x=-b生F-4ac 2 极点：S-50,±a,P△=6-4ae(5-43#42 公=2wVg2-) △-2w2(52-1)1，→过阻尼，S2=-50.±0V2-1(负实根) v,IS] 51s2 +0 -Wn (b)

§3.3 二阶系统的时域响应 二阶系统：由二阶微分方程描述的系统。 许多高阶系统常近似为二阶系统来研究，所以具有重要意义。 一.典型的二阶系统的数学模型       2 0 2 2 : 2 n n i n n x S G S x S S S          阻尼比 ：无阻尼固有频率 令上式分母 0，得二阶系统的特征方程： 2 2 2 0 n n S S      2 4 2 b b ac x     2 极点：S 1 1 2，        n n   2 2 2 2 2 4 2 4 4 ( 1) n n n        b ac w w w   2 2 ( 1) wn     2 2 2 ( 1) 0     wn  2 1 2 2 (1)0 1, S 1 1 n n d n     j              欠阻尼 ， 有阻尼固有频率 欠阻尼情况下系统的时间响应具有震荡特性。 系统的响应 1 2 (2) 1, S ( )          临界阻尼， ， n n 一对负实根 均无振荡 2 1 2 (3) 1, S 1( )           过阻尼， ， n n 负实根 jw σ × × s2 s1 [S] jwd -jwd -ξwn jw × σ s1 s2 [S] -wn (a) (b)

m↑S) wn不 S2 S1 (c) (d) 图3.13复数域极值分布图 (4)5=0,→零阻尼，S2=±j0,(一对纯虚根) 此时系统的时间响应为持续的等幅振荡。 二阶系统的响应特性完全由5和0，来描述。 二、二阶系统的单位阶跃响应 0=1401-日 x(S)=G(S)5s+25m3+a23 02 1 1当0<5<1，欠阻尼 S2=-50n±j0V-5-50±j0 002 6例-写+2编s+55+a+回js+a-回3 5(() S+50。 50。 M,-25-月 即：x(0=1-e5%cos0,1+ 5

jw × σ s2 s1 [S] × jw σ × s2 s1 [S] wn × (c) (d) 图 3.13 复数域极值分布图 1 2 (4) 0, S ( ) n       零阻尼， ， j 一对纯虚根 此时系统的时间响应为持续的等幅振荡。 二阶系统的响应特性完全由  和 n 来描述。 二、二阶系统的单位阶跃响应         2 0 2 2 1 1, [ ] 1 1 2 i i n n n x t L x t S x S G S S S S S             1. 0 1, 当    欠阻尼 2 S 1 1 2 n n n d ，             j j      2 2 0 2 2 1 1 2 n n n n n d n d x S S S S S j S j S                       2 2 2 2 1 n n n d n d S S S S               2 1 2 1 M r     0   2 1 cos sin 1 n n t t d d x t e t e t                        即：   2 0 2 1 1 sin arctan 1 n t d e x t t                     或：