内蒙古科技大学：《材料力学》课程PPT教学课件（机械类）第六章 弯曲变形

第六章弯曲变形目录

1 弯 曲 变 形 第 六 章 目录

第六章弯曲变形s6-1概述s6-2挠曲线的近似微分方程s6-3用积分法求弯曲变形s6-4用叠加法求弯曲变形S6-5简单超静定梁86-6梁的刚度条件及提高梁刚度的措施目录

2 第六章 弯曲变形 §6-1 概述 §6-2 挠曲线的近似微分方程 §6-3 用积分法求弯曲变形 §6-4 用叠加法求弯曲变形 §6-6 梁的刚度条件及提高梁刚度的措施 §6-5 简单超静定梁 目录 目录

s6-1 概述目录

3 §6-1 概 述 7-1 目录

s6-1 概述目录

4 §6-1 概 述 目录

s6-1概述目录

5 §6-1 概 述 目录

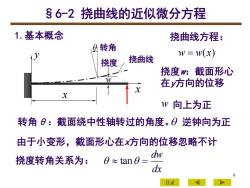
86-2挠曲线的近似微分方程1.基本概念挠曲线方程：四转角w= w(x)V挠曲线挠度挠度w：截面形心W在y方向的位移xxw向上为正转角θ：截面绕中性轴转过的角度。θi逆钟向为正由于小变形，截面形心在x方向的位移忽略不计dv度转角关系为：0~ tan0:dx目录

6 §6-2 挠曲线的近似微分方程 1.基本概念 挠曲线方程： w = w(x) 由于小变形，截面形心在x方向的位移忽略不计 挠度转角关系为： dx dw   tan = 挠曲线 y x x w 挠度  转角 挠度w：截面形心 在y方向的位移 w 向上为正 转角θ：截面绕中性轴转过的角度。  逆钟向为正 7-2 目录

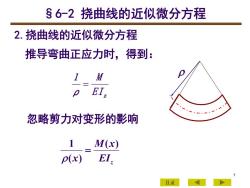
s6-2曲线的近似微分方程2.曲线的近似微分方程推导弯曲正应力时，得到：M7EI,0忽略剪力对变形的影响1M(x)EI,p(x)7目录

7 2.挠曲线的近似微分方程 推导弯曲正应力时，得到： E I z M ρ 1 = 忽略剪力对变形的影响 EIz M x x ( ) ( ) 1 =   目录 §6-2 挠曲线的近似微分方程

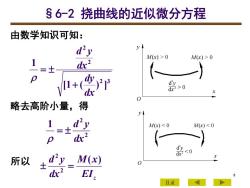
s6-2挠曲线的近似微分方程由数学知识可知：yd'yM(x) >0M(x)> 0dr?+O[1+()j3dy>0xdx0略去高阶小量，得yId22M(x)<0M(x) <0dr?pd'y<0dxxM(x)所以10?dr?EL,目录

8 由数学知识可知： 2 3 2 2 [1 ( ) ] 1 dx dy dx d y + =   略去高阶小量，得 2 2 1 dx d y =   所以 EIz M x dx d y ( ) 2 2  = 2 M(x) > 0 M(x) > 0 O d y dx 2 > 0 x y M(x) < 0 O dx d y 2 < 0 2 y x M(x) < 0 目录 §6-2 挠曲线的近似微分方程

86-2挠曲线的近似微分方程由弯矩的正负号规定可得，弯矩的符号与挠曲线的二阶导数符号一致，所以挠曲线的近似微分方程为：dwM(x)dx?EI由上式进行积分，就可以求出梁横截面的转角和挠度。目录

9 由弯矩的正负号规定可得，弯矩的符号与挠曲 线的二阶导数符号一致，所以挠曲线的近似微分方 程为： EI z M x dx d w ( ) 2 2 = 由上式进行积分，就可以求出梁横截面的转角 和挠度。 目录 §6-2 挠曲线的近似微分方程

86-2挠曲线的近似微分方程挠曲线的近似微分方程为：M(x)1EIM(x)Edrdx积分一次得转角方程为：d= EI,0 =[ M(x)dx+CEIdx再积分一次得挠度方程为：EI,w= JJ M(x)dxdx+Cx + DC目录

10 挠曲线的近似微分方程为： EI z M x dx d w ( ) 2 2 = 积分一次得转角方程为：  = EI = M x dx +C dx dw EIz z  ( ) ( ) 2 2 M x dx d w EIz = 再积分一次得挠度方程为： EIz w =  M (x)dxdx+Cx + D 7-3 目录 §6-2 挠曲线的近似微分方程