内蒙古科技大学：《工程力学》课程授课教案（讲义）第2章 平面简单力系

第2章教学方案-平面简单力系平面汇交力系的合成与平衡基本内容力对点之矩，合力矩定理力偶，平面力偶系的简化与平衡、掌握平面汇交力系的合成和平衡方程，求解未知力。教学目掌握力对点之矩，合力矩定理。的掌握力偶系的简化与平衡条件。重点平面汇交力系和力偶系的合成与平衡。、难点

第 2 章 教学方案 ——平面简单力系 基 本 内 容 平面汇交力系的合成与平衡 力对点之矩，合力矩定理 力偶，平面力偶系的简化与平衡 教 学 目 的 1、掌握平面汇交力系的合成和平衡方程，求解未知力。 2、掌握力对点之矩，合力矩定理。 3、掌握力偶系的简化与平衡条件。 重 点 、 难 点 平面汇交力系和力偶系的合成与平衡

第2章平面简单力系当力系中的各力作用线都在同一平面上时，该力系称为平面力系。若平面力系中各力作用线通过同一点时，该力系称为平面汇交力系：若平面力系中的各力均成对构成力偶时，称该力系为平面力偶系。通常将平面汇交力系和平面力偶系称为平面简单力系。2.1平面汇交力系的合成与平衡2.1.1 平面汇交力系合成与平衡的几何法合成依据：力的平行四边形法则或三角形法则。如果是由多个力构成的平面汇交力系，用多边形法则。●方法：将力Fi，…，Fa依次首尾相接，形成一条折线，连接其封闭边，即从Fi的始端指向F4的末端所形成的矢量即为合力，如图2.1（c）所示，此法称为力的多边形法则。fa)(d)图2.1·结论：平面汇交力系可以合成为一个合力，该合力等于力系各力的矢量和，合力的作用线通过汇交点。合力FR可用矢量式表示为FR =F+F,+F,-ZF(2-1)画力多边形时，改变各分力相加的次序，将得到形状不同的力多边形，但最后求得的合力不变，如图2.1（d）所示。·平衡条件：平面汇交力系平衡的充分和必要条件是；该力系的合力等于零。以矢量等式表示为25=0(2-2)平衡的几何条件；平面汇交力系的力多边形自行封闭。【例2-1】支架ABC由横杆AB与支撑杆BC组成，如图2.2（a）所示。A、B、C处均为铰链连接，B端悬挂重物，其重力W=5kN，杆重不计，试求两杆所受的力。解：（1）选择研究对象，以销子B为研究对象（2）受力分析，画受力图。由于AB、BC杆均为二力杆，两端所受的力的作用线必过直杆的轴线。FI、Fz、W组成平面汇交力系，其受力图如图2.2（b）所示。（3）根据平衡几何条件求出未知力。当销子平衡时，三力组成一封闭力三角形，先画W

第 2 章 平面简单力系 当力系中的各力作用线都在同一平面上时，该力系称为平面力系。若平面力系中各力 作用线通过同一点时，该力系称为平面汇交力系；若平面力系中的各力均成对构成力偶时， 称该力系为平面力偶系。通常将平面汇交力系和平面力偶系称为平面简单力系。 2.1 平面汇交力系的合成与平衡 2.1.1 平面汇交力系合成与平衡的几何法 ●合成依据：力的平行四边形法则或三角形法则。如果是由多个力构成的平面汇交力系， 用多边形法则。 ●方法：将力 F1，.，F4 依次首尾相接，形成一条折线，连接其封闭边，即从 F1 的 始端指向 F4 的末端所形成的矢量即为合力，如图 2.1（c）所示，此法称为力的多边形法则。 图 2.1 ●结论：平面汇交力系可以合成为一个合力，该合力等于力系各力的矢量和，合力的作 用线通过汇交点。合力 FR 可用矢量式表示为 = = + + + = n i R n i 1 F F1 F2  F F （2-1） 画力多边形时，改变各分力相加的次序，将得到形状不同的力多边形，但最后求得的合 力不变，如图 2.1（d）所示。 ●平衡条件：平面汇交力系平衡的充分和必要条件是：该力系的合力等于零。以矢量等 式表示为 （2-2） ●平衡的几何条件：平面汇交力系的力多边形自行封闭。 【例 2-1】支架 ABC 由横杆 AB 与支撑杆 BC 组成，如图 2.2（a）所示。A、B、C 处 均为铰链连接，B 端悬挂重物，其重力 W = 5kN，杆重不计，试求两杆所受的力。 解：（1）选择研究对象，以销子 B 为研究对象。 （2）受力分析，画受力图。由于 AB、BC 杆均为二力杆，两端所受的力的作用线必过 直杆的轴线。F1、F2、W 组成平面汇交力系，其受力图如图 2.2（b）所示。 （3）根据平衡几何条件求出未知力。当销子平衡时，三力组成一封闭力三角形，先画 W ， 1 0 n i i F =  =

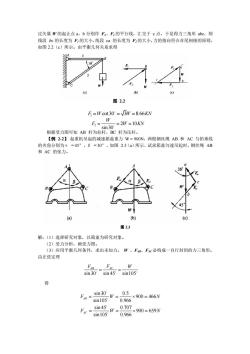
过矢量W的起止点a、b分别作F2、F,的平行线，汇交于c点，于是得力三角形abc，则线段 bc 的长度为Fi的大小，线段 ca 的长度为F的大小，力的指向符合首尾相接的原则，如图2.2（c）所示。由平衡几何关系求得图2.2F =Wcot30°=/3W=8.66KNWF==2W=10KNsin30根据受力图可知AB杆为拉杆，BC杆为压杆。【例2-2】起重机吊起的减速箱盖重力W=900N，两根钢丝绳AB和AC与铅垂线的夹角分别为α=45°，β=30°，如图2.3（a）所示，试求箱盖匀速吊起时，钢丝绳AB和AC的张力。(a)(b)图 2.3解：（1）选择研究对象，以箱盖为研究对象。（2）受力分析，画受力图（3）应用平衡几何条件，求出未知力。W、FAB、FAc必构成一自行封闭的力三角形。由正弦定理o-slsW=sin30 = 0.5900=466NFABsin1050.966=0.707×900= 659Nsin45_w=FAc=sin1050.966

1F W W KN = = = cot30 3 8.66 2 2 10 sin30 W F W KN = = = 图 2.2 过矢量 W 的起止点 a、b 分别作 F2、F1 的平行线，汇交于 c 点，于是得力三角形 abc，则 线段 bc 的长度为 F1 的大小，线段 ca 的长度为 F2 的大小，力的指向符合首尾相接的原则， 如图 2.2（c）所示。由平衡几何关系求得 根据受力图可知 AB 杆为拉杆，BC 杆为压杆。 【例 2-2】 起重机吊起的减速箱盖重力 W = 900N，两根钢丝绳 AB 和 AC 与铅垂线 的夹角分别为α = 45°，β = 30°，如图 2.3（a）所示，试求箱盖匀速吊起时，钢丝绳 AB 和 AC 的张力。 解：（1）选择研究对象，以箱盖为研究对象。 （2）受力分析，画受力图。 （3）应用平衡几何条件，求出未知力。 W 、FAB、FAC必构成一自行封闭的力三角形。 由正弦定理 得 sin 30 sin 45 sin105 FAB FAC W = = sin 30 0.5 900 466 sin105 0.966 sin 45 0.707 900 659 sin105 0.966 AB AC F W N F W N = =  = = =  = 图 2.3

2.1.2力在直角坐标轴上的投影·概念：设在平面直角坐标系Oxy内有一已知力F，从力F的两端A和B分别向x、y轴作垂线，垂足a、b和a'、b之间的距离再加上适当的正负号分别称为力F在x轴和y轴上的投影，以X和Y表示。并且规定：当从力的始端投影到末端投影的方向与坐标轴的正向相同时，取正号，反之取负。图 2.4（a）中的x、Y均为正值，图2.4（b）中的X、为负值、Y为正值。所以，力在坐标轴上的投影是代数量。(a)(b)图 2.4·计算：力的投影的大小可用三角公式计算，设力F与x轴的正向夹角为α，则X=Fcosα(2-3)Y=Fsinα分力和投影的关系：如将力 F 沿 x、y坐标轴分解，所得分力F、F,的大小与力 F在同轴的投影X、Y的绝对值相等，但必须注意：力的投影与分力是两个不同的概念。力的投影是代数量，而分力是矢量。其关系可表示为F=F,+E,=Xi+Y(2-4)若已知力F在直角坐标轴上的投影X、Y，则可按下式求出该力的大小和方向余弦为F=x+y?(2-5)cosα=2.1.3合力投影定理由n个力构成的平面汇交力系，其合力可由（2-1）式求得。若将合力和各分力表示为式（2-4）的形式，即Fr=Fri+Fryj,F =X,i+Yj (i=-1,2...n)代入式(2-1）可得Fr=Fai+Frj-2xi+2Yj(2-6)即

图 2.4 2.1.2 力在直角坐标轴上的投影 ●概念：设在平面直角坐标系 Oxy 内有一已知力 F，从力 F 的两端 A 和 B 分别向 x、y 轴作垂线，垂足 a、b 和 a′、b′之间的距离再加上适当的正负号分别称为力 F 在 x 轴和 y 轴上的投影，以 X 和 Y 表示。并且规定：当从力的始端投影到末端投影的方向与坐 标轴的正向相同时，取正号，反之取负。图 2.4（a）中的 X、Y 均为正值，图 2.4（b）中 的 X、为负值、Y 为正值。所以，力在坐标轴上的投影是代数量。 ●计算：力的投影的大小可用三角公式计算，设力 F 与 x 轴的正向夹角为α，则 （2-3） ●分力和投影的关系：如将力 F 沿 x、y 坐标轴分解，所得分力 Fx、Fy的大小与力 F 在同轴的投影 X、Y 的绝对值相等，但必须注意：力的投影与分力是两个不同的概念。力 的投影是代数量，而分力是矢量。其关系可表示为 F F F Xi Yj = x + y = + （2-4） 若已知力 F 在直角坐标轴上的投影 X、Y，则可按下式求出该力的大小和方向余弦为 F X F X Y = = + cos 2 2 （2-5） 2.1.3 合力投影定理 由 n 个力构成的平面汇交力系，其合力可由（2-1）式求得。若将合力和各分力表示为 式（2-4）的形式，即 F F , X Y (i 1,2 n) FR = Rx i + Ry j Fi = i i + i j =  代入式（2-1）可得 F i j  i  j = = = + = + n i i n i R FRx FRy Xi Y 1 1 （2-6） 即 cos sin X F Y F   = =

V(2-7)?可得结论：合力在任一轴上的投影等于各分力在同一轴上的投影的代数和。这就是合力投影定理。2.1.4平面汇交力系合成与平衡的解析法●合成：设在刚体上的点O处，作用了由n个力Fi，F2，，F,组成的平面汇交力系，Xi和Y，X2和Y2，…，X和Yn分别表示力Fi，F2，，Fa在直角坐标轴Ox和Oy上的投影。根据合力投影定理，可求得合力FR在这两轴上的投影，如式（2-7）所示。已知力的投影，可以根据式（2-5）求得合力的大小和方向为Fr=F+F=Zx)+(Zm)(2-8)Zxcosα式中的α表示合力的正向与x轴所夹的角。【例2-3】一吊环受到三条钢丝绳的拉力，如图2.5（a）所示。已知Fi=2000N，平向左；Fz-2500N，与水平成30°角；F:=1500N，铅垂向下，试用解析法求合力的大小和方向。(6)fa图2解：以三力的交点0为坐标原点，建立直角坐标系如图2.5所示，先分别计算各力的投影。Fx =-F, =-2000NF2=-F,cos30=-2500×0.866=-2165NFI=0F,=0Fz, =-F, sin30°=-2500×0.5=-1250NF,=-F, =-1500N可得R, =F, =(-2000-2165+0)=-4165NR,=ZF,=(0-1250-1500)=-2750NR=R +R, = /-4165) +(-2750) =4991N

       = =   = = n i Ry i n i Rx i F Y F X 1 1 （2-7） 可得结论：合力在任一轴上的投影等于各分力在同一轴上的投影的代数和。这就是合力 投影定理。 2.1.4 平面汇交力系合成与平衡的解析法 ●合成：设在刚体上的点 O 处，作用了由 n 个力 F1，F2，.，Fn组成的平面汇交力 系，X1 和 Y1，X2 和 Y2，.，Xn 和 Yn 分别表示力 F1，F2，.，Fn 在直角坐标轴 Ox 和 Oy 上的投影。根据合力投影定理，可求得合力 FR 在这两轴上的投影，如式（2-7）所示。 已知力的投影，可以根据式（2-5）求得合力的大小和方向为 R R Rx Ry F X F F F X Y    = = + = + cos ( ) ( ) 2 2 2 2 （2-8） 式中的α 表示合力的正向与 x 轴所夹的角。 【例 2-3】 一吊环受到三条钢丝绳的拉力，如图 2.5（a）所示。已知 F1=2000N，水 平向左；F2=2500N，与水平成 30°角；F3=1500N，铅垂向下，试用解析法求合力的大小和 方向。 图 2.5 解：以三力的交点 O 为坐标原点，建立直角坐标系如图 2.5 所示，先分别计算各力的 投影。 可得 1 1 2 2 3 1 2 2 3 3 2000 cos30 2500 0.866 2165 0 0 sin 30 2500 0.5 1250 1500 X x x y y y F F N F F N F F F F N F F N = − = − = − = −  = − = = = − = −  = − = − = − 2 2 2 2 ( 2000 2165 0) 4165 (0 1250 1500) 2750 ( 4165) ( 2750) 4991 x x y y x y R F N R F N R R R N = = − − + = − = = − − = − = + = − + − =  

由于R和R都是负值，所以合力R应在第三象限，如图2.5（b）所示。[R,_2750= 0.660ano4165α= 33.4°●平衡方程：平面汇交力系平衡的充分必要条件是力系的合力等于零。根据（2-8）式，当合力为零时，有2X=0l(2-9)ZY=0即，平面汇交力系平衡的充分必要条件是各力在两个正交坐标轴上投影的代数和分别为零。式（2-9）称为平面汇交力系的平衡方程。平面汇交力系有两个独立的平衡方程，可求解两个未知量，可以是力的大小，也可以是力的方向。【例2-4】简易起重装置如图2.6（a）所示，重物吊在钢丝绳的一端，钢丝绳的另一端跨过定滑轮A，绕在绞车D的鼓轮上，定滑轮用直杆AB和AC支承，定滑轮半径较小，其大小可忽略不计，设重物重W=2kN，定滑轮、各直杆以及钢丝绳的重量不计，各处接触均为光滑。试求匀速提升重物时，杆AB和AC所受的力。(a)(b)图 2.6解：选取滑轮为研究对象。滑轮的受力图如图2.6（b）所示。其中只有NAs和Nac的大小未知，两个未知数可由平面汇交力系平衡方程解出，AZF,=0NAcsin30°-Fcos30°-W=0得W+Fcos30~_2+20.866=7.46KNNACsin30°0.5再由ZF=0-NAB+NAc cos30°-Fsin30°=0可得NAB=Naccos30°-F sin30°=7.46×0.866-2×0.5= 5.46KN两力求出均为正值，说明其方向与所假设方向一致。【例2-5】压榨机简图如图2.7（a）所示，在铰链A处作用一水平力F使压块C压紧物体D。若杆AB和AC的重量忽略不计，各处接触均为光滑，求物体D所受的压力

由于 Rx 和 Ry 都是负值，所以合力 R 应在第三象限，如图 2.5（b）所示。 ●平衡方程：平面汇交力系平衡的充分必要条件是力系的合力等于零。根据（2-8）式， 当合力为零时，有    = =   0 0 Y X （2-9） 即，平面汇交力系平衡的充分必要条件是各力在两个正交坐标轴上投影的代数和分别为零。 式（2-9）称为平面汇交力系的平衡方程。平面汇交力系有两个独立的平衡方程，可求 解两个未知量，可以是力的大小，也可以是力的方向。 【例 2-4】 简易起重装置如图 2.6（a）所示，重物吊在钢丝绳的一端，钢丝绳的另一 端跨过定滑轮 A，绕在绞车 D 的鼓轮上，定滑轮用直杆 AB 和 AC 支承，定滑轮半径较小， 其大小可忽略不计，设重物重 W=2kN，定滑轮、各直杆以及钢丝绳的重量不计，各处接触 均为光滑。试求匀速提升重物时，杆 AB 和 AC 所受的力。 解：选取滑轮为研究对象。滑轮的受力图如图 2.6（b）所示。其中只有 NAB和 NAC的 大小未知，两个未知数可由平面汇交力系平衡方程解出。 由 得 再由 可得 两力求出均为正值，说明其方向与所假设方向一致。 【例 2-5】 压榨机简图如图 2.7（a）所示，在铰链 A 处作用一水平力 F 使压块 C 压紧 物体 D。若杆 AB 和 AC 的重量忽略不计，各处接触均为光滑，求物体 D 所受的压力。 2750 tan 0.660 4165 33.4 y x R R   = = = = 0 sin30 cos30 0 F N F W y AC = − − = cos30 2 2 0.866 7.46 sin 30 0.5 AC W F N KN + +  = = = 0 cos30 sin30 0 F N N F x AB AC = − + − = cos30 sin 30 7.46 0.866 2 0.5 5.46 N N F KN AB AC = − =  −  = 图 2.6

(b)(0)(a)图 2.7 解：先取铰链A为研究对象，设二力杆AB和AC均受拉力，因此铰链A的受力图如图2.7（b）所示。为了减少方程中未知力的个数，投影轴应尽量取在与未知力作用线相垂直的方向。这样在列平衡方程式时，该未知数不出现在方程中。建立如图2.7（b）所示坐标系，列出平衡方程ZF=0-Fcosα-Nccos(90°-2α)=0NAc =-F COSα_2sinαsin2α解出结果为负值表示该力的实际方向与图中所假设方向相反。再选取压块为研究对象，画受力图，建立坐标系，如图2.7（c）所示。因为AC杆为二力杆，A、C两端的作用力相等，方向可以用二力平衡条件确定。列平衡方程ZF,=0NAc cosα+N = 0NIC=N.Fcotα_Fl)cosα:NCcosα=2h2sin2通过以上的例题，归纳出平面汇交力系平衡方程应用的主要步骤和注意事项如下：（1）所选择的研究对象应作用有已知力（或已经求出的力）1.选择研究对象时应注意：和未知力，这样才能应用平衡条件由已知力求得未知力：（2）先以受力简单并能由已知力求得未知力的物体作为研究对象，然后再以受力较为复杂的物体作为研究对象。2.取分离体，画受力图。研究对象确定之后，需要分析受力情况。为此，需将研究对象从其周围物体中分离出来。根据所受的外载荷画出分离体所受的主动力：根据约束性质，画出分离体所受的约束力，最后得到研究对象的受力图选取坐标系，计算力系中所有的力在坐标轴上的投影。坐标轴可以任意选择，但应尽量使坐标轴与未知力平行或垂直，可以使力的投影简便，同时使平衡方程中包括最少数目的未知量，避免解联立方程。4.列平衡方程，求解未知量。若求出的力为正值，则表示受力图上所假设的力的指向与实际指向相同：若求出的力为负值，则表示受力图上力的实际指向与所假设的指向相反，在受力图上不必改正。在答案中要说明力的方向。2.2力对点之矩合力矩定理

图 2.7 解：先取铰链 A 为研究对象，设二力杆 AB 和 AC 均受拉力，因此铰链 A 的受力图 如图 2.7（b）所示。为了减少方程中未知力的个数，投影轴应尽量取在与未知力作用线相 垂直的方向。这样在列平衡方程式时，该未知数不出现在方程中。建立如图 2.7（b）所示坐 标系，列出平衡方程 得 解出结果为负值表示该力的实际方向与图中所假设方向相反。 再选取压块 C 为研究对象，画受力图，建立坐标系，如图 2.7（c）所示。因为 AC 杆 为二力杆，A、C 两端的作用力相等，方向可以用二力平衡条件确定。列平衡方程 且 通过以上的例题，归纳出平面汇交力系平衡方程应用的主要步骤和注意事项如下： 1.选择研究对象时应注意：（1）所选择的研究对象应作用有已知力（或已经求出的力） 和未知力，这样才能应用平衡条件由已知力求得未知力；（2）先以受力简单并能由已知力求 得未知力的物体作为研究对象，然后再以受力较为复杂的物体作为研究对象。 2.取分离体，画受力图。研究对象确定之后，需要分析受力情况。为此，需将研究对象 从其周围物体中分离出来。根据所受的外载荷画出分离体所受的主动力；根据约束性质，画 出分离体所受的约束力，最后得到研究对象的受力图。 3.选取坐标系，计算力系中所有的力在坐标轴上的投影。坐标轴可以任意选择，但应尽 量使坐标轴与未知力平行或垂直，可以使力的投影简便，同时使平衡方程中包括最少数目的 未知量，避免解联立方程。 4.列平衡方程，求解未知量。若求出的力为正值，则表示受力图上所假设的力的指向与 实际指向相同；若求出的力为负值，则表示受力图上力的实际指向与所假设的指向相反，在 受力图上不必改正。在答案中要说明力的方向。 2.2 力对点之矩 合力矩定理 0 cos cos(90 2 ) 0 F F N x AC = − − − =   cos sin 2 2sin AC F N F    = − = − / 0 cos 0 F N N y AC = + =  / cot cos ( )cos 2sin 2 2 AC AC AC N N F F Fl N N h     = − = − = − = =

2.2.1力对点之矩力对点0 的矩的概念：：作用在物体上的力使物体绕某一点转动效果的度量。●力对点0的矩的计算：如用扳手柠螺母，作用于扳手上的力F使扳手绕固定点O转动，如图2.8所示。力F使扳手绕0点转动的效果，取决于两个因素：力的大小与O点到该力作用线垂直距离的乘积（F·h）和力使扳手绕O点转动的方向。可一个代数量±Fh来表示，称为力对点0的矩，简称力矩。用公式记为FMo(F)=±Fh(2-10)图2.82点称为力矩中心，简称矩心：距离h称为力臂。在平面间题中，力对点的矩是一个代数量，力矩的大小等于力的大小与力臂的乘积。其正负号表示力使物体绕矩心转动的方向。通常规定：力使物体作逆时针方向转动时力矩为正，反之为负。力矩的单位在国际单位制中为牛顿米（N·m），或千牛顿米（kN·m）。由式（2-10）可知，力矩在下列两种情况下等于零：（1）力的大小为零：（2）力臂等于零，即力的作用线通过矩心。2.2.2合力矩定理●合力矩定理：如果平面力系Fi、F、、F,可以合成为一个合力FR，则可以证明Mo(Fr)= M。(F)+Mo(F,)+..+ M。(F.)=ZMo(F)(2-11)这表明：平面力系的合力对平面内任一点的矩等于力系中各分力对于同一点力矩的代数和，这一结论称为合力矩定理。●合力矩定理应用：（1）力矩计算的解析表达式：如图2.9所示，已知力F作用点A（x、y)，求力F对坐标原点O的矩。根据合力矩定理，力F对坐标原点O的矩等于力F的两个分力F和F,对坐标原点O 的矩的代数和。即Mo(F)= Mo(F:)+ Mo(F,)= xE, - yFx或(2-12)Mo(F)=xY-JX其中X、Y为力F在x、y轴上的投影。图 2.9

图 2.9 2.2.1 力对点之矩 ●力对点 O 的矩的概念：作用在物体上的力使物体绕某一点转动效果的度量。 ●力对点 O 的矩的计算：如用扳手拧螺母，作 用于扳手上的力 F 使扳手绕固定点 O 转动，如图 2.8 所示。力 F 使扳手绕 O 点转动的效果，取决于 两个因素：力的大小与 O 点到该力作用线垂直距离 的乘积（F·h）和力使扳手绕 O 点转动的方向。可 用一个代数量±Fh 来表示，称为力对点 O 的矩，简 称力矩。用公式记为 MO (F) = Fh （2-10） O 点称为力矩中心，简称矩心，距离 h 称为力 臂。在平面问题中，力对点的矩是一个代数量，力矩的大小等于力的大小与力臂的乘积。其 正负号表示力使物体绕矩心转动的方向。通常规定：力使物体作逆时针方向转动时力矩为正， 反之为负。 力矩的单位在国际单位制中为牛顿米（N·m），或千牛顿米（kN·m）。由式（2-10） 可知，力矩在下列两种情况下等于零： （1）力的大小为零； （2）力臂等于零，即力的作用线通过矩心。 2.2.2 合力矩定理 ●合力矩定理：如果平面力系 F1、F2、.、Fn 可以合成为一个合力 FR，则可以证明 ( ) ( ) ( ) ( ) ( ) 1 F F1 F2 Fn  Fi = = + + + = n i MO R MO MO  MO MO （2-11） 这表明：平面力系的合力对平面内任一点的矩等于力系中各分力对于同一点力矩的代数和。 这一结论称为合力矩定理。 ●合力矩定理应用： （1）力矩计算的解析表达式：如图 2.9 所示，已知力 F 作用点 A（x、y），求力 F 对坐 标原点 O 的矩。根据合力矩定理，力 F 对坐标原点 O 的矩等于力 F 的两个分力 Fx和 Fy对 坐标原点 O 的矩的代数和。即 O O O y x M (F) = M (Fx ) + M (Fy ) = x F − yF 或 MO (F) = xY − yX （2-12） 其中 X、Y 为力 F 在 x、y 轴上的投影。 图 2.8

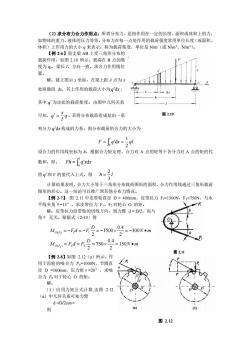
（2）求分布力合力作用点：所谓分布力，是指作用在一定的长度、面积或体积上的力，如物体的重力、液体的压力等等。分布力在每一点处作用的载荷强度常用单位长度（或面积体积）上作用力的大小q来表示，称为载荷集度，单位是N/m（或 N/m2、N/m2)。【例2-6】简支梁AB上受三角形分布的载荷作用，如图2.10所示。载荷在B点的集度为q0，梁长1。方向一致。求合力作用线位置解：建立图示×坐标，在梁上距A点为处取微段dx，其上作用的载荷大小为q'dx，其中q'为该处的载荷集度。由图中几何关系图 2.10可知，q9。若将分布载荷看成是由一系列分力q'dx构成的力系，则分布载荷的合力的大小为F=Il'q'dx={ql设合力的作用线坐标为h，根据合力矩定理，合力对A点的矩等于各分力对A点的矩的代Fh= I'q'xdx数和，即：将q和F的值代入上式，得h=21计算结果表明，合力大小等于三角形分布载荷图形的面积，合力作用线通过三角形载荷图形的形心。这一结论可以推广到其他分布力情况。【例2-7】图2.11中皮带轮直径D=400mm，皮带拉力Fi=1500N，F2=750N，与水平线夹角 α=15°。求皮带拉力 FI、F2对轮心O的矩。解：皮带拉力沿带轮的切线方向，则力臂d=D/2，而与角无关。根据式（2-10）得0.4Mo(5)=-Fd=-FD=-1500-300N·nx04=150NomMo(5)=F,d=F号=750x图2.11【例2-8】如图2.12（a）所示，作P用于齿轮的啮合力P,=1000N，节圆直径D=160mm，压力角α=20°，求啮合力Pn对于轮心O的矩。（1）应用力矩公式计算，由图2.12（a）中几何关系可知力臂d =D/2cos a(a)(b则图 2.12

图 2.12 （2）求分布力合力作用点：所谓分布力，是指作用在一定的长度、面积或体积上的力， 如物体的重力、液体的压力等等。分布力在每一点处作用的载荷强度常用单位长度（或面积、 体积）上作用力的大小 q 来表示，称为载荷集度，单位是 N/m（或 N/m2、N/m3）。 【例 2-6】简支梁 AB 上受三角形分布的 载荷作用，如图 2.10 所示。载荷在 B 点的集 度为 q0，梁长 l。方向一致。求合力作用线位 置。 解：建立图示 x 坐标，在梁上距 A 点为 x 处取微段 dx，其上作用的载荷大小为 q dx ， 其中 q  为该处的载荷集度。由图中几何关系 可知， q l x q  = 。若将分布载荷看成是由一系 列分力 q dx 构成的力系，则分布载荷的合力的大小为  =  = l F q x ql 0 2 1 d 设合力的作用线坐标为 h，根据合力矩定理，合力对 A 点的矩等于各分力对 A 点的矩的代 数和，即：  =  l Fh q x x 0 d 将 q  和 F 的值代入上式，得 h l 3 2 = 计算结果表明，合力大小等于三角形分布载荷图形的面积，合力作用线通过三角形载荷 图形的形心。这一结论可以推广到其他分布力情况。 【例 2-7】 图 2.11 中皮带轮直径 D = 400mm，皮带拉力 F1=1500N，F2=750N，与水 平线夹角θ=15°。求皮带拉力 F1、F2 对轮心 O 的矩。 解：皮带拉力沿带轮的切线方向，则力臂 d = D/2，而与 角θ 无关。根据式（2-10）得 【例 2-8】如图 2.12（a）所示，作 用于齿轮的啮合力 Pn=1000N，节圆直 径 D =160mm，压力角α=20°，求啮 合力 Pn 对于轮心 O 的矩。 解： （1）应用力矩公式计算,由图 2.12 （a）中几何关系可知力臂 d =D/2cosα 则 1 2 ( ) 1 1 ( ) 2 2 0.4 1500 300 2 2 0.4 750 150 2 2 O F O F D M F d F N m D M F d F N m = − = − = −  = − • = = =  = • 图 2.11 图 2.10

Mo(P)=-P,d=-1000 016ecos20 =-75.2Nom（2）应用合力矩定理计算将啮合力P.正交分解为圆周力P和径向力P，如图2.12（b）所示，可知节圆半径是圆周力的力臂，根据合力矩定理，得0.16=-75.2Nm2+0=-1000cos20Mo(P,)= M。(P)+ M。(P,)=-P, cosα工程中齿轮的圆周力和径向力是分别给出的，因此第二种方法较为普遍。2.3力偶平面力偶系的简化与平衡2.3.1力偶的概念●力偶的概念：由大小相等、方向相反、作用线相距一段距离的两个平行力F与F组成的力系称为力偶，通常用符号（F，F’）表示。两力作用线所决定的平面称为力偶的作用面，而力作用线间的垂直距离称为力偶臂。在工程实际中，常见力偶作用的例子，如用丝锥攻丝和转动方向盘等都是受到力偶的作用，如图2.13所示。F(a)(b)图2.13力偶的计算：构成力偶的两个等值反向平行力的合力显然等于零，但它们不能相互平衡，而是使物体产生转动效应。因此，力和力偶是静力学的两个基本作用量。力偶不能合成为一个力或用一个力来平衡。力偶对物体的转动效果，可用构成力偶的两个力对其作用面内某点的矩的代数和来度量。设有力偶（F，F），其力偶臂为d，如图2.14所示。力偶对作用面内的任一点O的矩为m。F,F")，则m,(F,F")=m,(F)+m.(F)(2-13)= F-ao- F'.bo= F(ao-bo)= Fd因为矩心O是任意选取的，由此可知，力偶的作用效果决定于力的大小和力偶臂的乘积，与矩心的位置无关。力与力偶臂的乘积称为力偶矩，记作m（F，F"），简记为m。力偶在平面内的转向不同，作用效果也不同。因此，力偶对物体的作用效果，由力偶矩的大小和力偶在作用平面内的转向两个因素决定。若把力偶矩视为代数量，规定逆时针转向为正，顺时针转向为负，则

0.16 ( ) 1000 cos 20 75.2 2 M P P d N m O n n = − = −  = − • （2）应用合力矩定理计算 将啮合力 Pn 正交分解为圆周力 P 和径向力 Pr，如图 2.12（b）所示，可知节圆半径 是圆周力的力臂，根据合力矩定理，得 0.16 ( ) ( ) ( ) cos 0 1000cos 20 75.2 2 2 O n O O r n D M P M P M P P N m = + = − + = −  = − •  工程中齿轮的圆周力和径向力是分别给出的，因此第二种方法较为普遍。 2.3 力偶 平面力偶系的简化与平衡 2.3.1 力偶的概念 ●力偶的概念：由大小相等、方向相反、作用线相距一段距离的两个平行力 F 与 F 组 成的力系称为力偶，通常用符号（F，F′）表示。两力作用线所决定的平面称为力偶的作 用面，而力作用线间的垂直距离称为力偶臂。在工程实际中，常见力偶作用的例子，如用丝 锥攻丝和转动方向盘等都是受到力偶的作用，如图 2.13 所示。 图 2.13 ●力偶的计算：构成力偶的两个等值反向平行力的合力显然等于零，但它们不能相互平 衡，而是使物体产生转动效应。因此，力和力偶是静力学的两个基本作用量。力偶不能合成 为一个力或用一个力来平衡。 力偶对物体的转动效果，可用构成力偶的两个力对其作用面内某点的矩的代数和来度 量。设有力偶（F，F′），其力偶臂为 d，如图 2.14 所示。力偶对作用面内的任一点 O 的 矩为 ( , ) m F F o  ，则 ( , ) ( ) ( ) ( ) m F F m F m F o o o F ao F bo F ao bo Fd   = + = −  = − = 因为矩心 O 是任意选取的，由此可知，力偶的作用效果决定于力的大小和力偶臂的乘 积，与矩心的位置无关。力与力偶臂的乘积称为力偶矩，记作 m（F，F′），简记为 m。 力偶在平面内的转向不同，作用效果也不同。因此，力偶对物体的作用效果，由力偶矩的大 小和力偶在作用平面内的转向两个因素决定。 若把力偶矩视为代数量，规定逆时针转向为正，顺时针转向为负，则 （2-13）