《工程力学》课程教学课件（PPT讲稿）第一篇 工程静力学 第4章 空间力系

第四章空间力系

1

静力学各力的作用线不在同一平面内的力系，叫空间力系，空间力系是最一般的力系。分为：空间汇交力系（α图）：空间任意力系(b图）空间平行力系(b图中去了风力）等。迎面Q1风力SYSOy工侧面PI风力NN(a)

2 各力的作用线不在同一平面内的力系，叫空间力系，空间 力系是最一般的力系。 分为： 空间汇交力系（a图）；空间任意力系(b图）； 空间平行力系(b图中去了风力）等。 迎 面 风 力 侧 面 风 力 b

静力学$4-1空间汇交力系、力在空间轴上的投影与分解：Z1、一次投影法（直接投影法）已知: α,β,X=F.cos α,Y=F-cos β,Z=F-cos yy2、二次投影法（间接投影法）H已知：Φ,0xiX -F-siny-cosp=Fr-cosp-F-coso.cospY-F-siny·sin@=F-sin@=F-.coso.sinpZ-F-cosy=F.sino2

3 一、力在空间轴上的投影与分解： §4-1 空间汇交力系    cos cos , cos , =  =  =  Z F Y F X F 1、一次投影法（直接投影法） 已知： ,,  2、二次投影法（间接投影法） 已知： ,  X =Fsin cos =Fxy cos =Fcos cos Y =Fsin sin =Fxy sin =Fcos sin Z =Fcos =Fsin

静力学3、力沿坐标轴分解+Z若以F,F,F表示力沿直角坐标轴的正交分量，则：F-F+F,+FFy而:yKF6F.- Xi,F,-Yi.F -Zk七y所以:F= Xi +Yi+Zk.F=X2+Y2+Z?cosα-→.cosβ-1,.cosy-

4 3、力沿坐标轴分解： 若以 表示力沿直角 坐标轴的正交分量，则： Fx Fy Fz , , F =Fx +Fy +Fz 2 2 2 F= X +Y +Z F Z F Y F X cos= ,cos = ,cos = F Xi F Yj F Zk x = , y = , z = 而： 所以： F =Xi +Yj+Zk Fx Fy Fz

静力学二、空间汇交力系的合成：设空间汇交力系由 FF,F·..,F组成。则其合力为R-F+F2+F3+...+F, -ZF由于 F=Xi+Yi+Z,k 代入上式合力 R-ZX,i+ZYj+z,kR,-ZXR,-ZY由X，为合力在x轴的投影，.R.-Z合力投影定理合力;R-/R? +R2 +R2 =N(EX)? +(ZY)? +(Z)?00-0--号00-号RR

5 R=F1 +F2 +F3 ++Fn =F i 由于 代入上式 合力 由 为合力在x轴的投影， ∴ F X i Y j Z k i = i + i + i R X i Y j Z k = i + i + i Xi Rx =Xi Ry =Yi Rz =Zi 二、空间汇交力系的合成： 设空间汇交力系由 F1 , F2 , F3  , Fn 组成。则其合力为 ——合力投影定理 = 2 + 2 + 2 =  2 +  2 +  2 :R R R R ( X) ( Y) ( Z) 合力 x y z R R R R R Rx y z cos= ,cos == ,cos =

静力学三、空间汇交力系的平衡空间汇交力系平衡的充要条件是：力系的合力为零，即：X=0即：R-F-0空间汇交力系的平衡方程ZY=0z=0[例1已知： AB=3m,AE=AF-4m,O-20kN求:绳BE、BF的拉力和杆AB的内力y解：分别研究C点和B点作受力图HTi'X由C点：ZY=0,T'sin15°-Qsin45°=0oQ45°..T -546(kN)QMi

6 三、空间汇交力系的平衡： R =Fi =0 空间汇交力系平衡的充要条件是：力系的合力为零，即： X =0 Y =0 Z =0 即： 空间汇交力系的平衡方程 [例] 已知：AB=3m,AE=AF=4m, Q=20kN; 求:绳BE、BF的拉力和杆AB的内力 解：分别研究C点和B点作受力图 546(kN) 0, 'sin15 sin45 0, 1 1  =  = −  = T 由C点： Y T Q

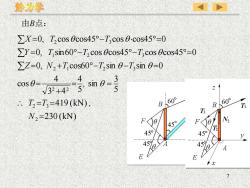
静力学由B点：ZX=0, T, cos Ocos45°-T,cos O-.cos45°=0ZY =0, T, sin60°-T, cos Ocos45°-T,cos cos45°=0Z=0, N,+T cos60°-T,sin 0-T,sin 0=0443cos O=V32 +4273: sin 0 =5ZBL60°60°T, =T,-419(kN),BTiT3N,=230 (kN)N2F0F<014545945°y45%4506ADEE/ x7

7 230 (kN) 419 (kN), 5 3 , sin 5 4 3 4 4 cos 0, cos60 sin sin 0 0, sin60 cos cos45 cos cos45 0 0, cos cos45 cos cos45 0 2 2 3 2 2 2 1 2 3 1 2 3 2 3 =  = = = = + = = + − − = = − − = = −  =    N T T Z N T T T Y T T T X T T         由B点：

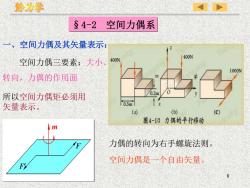
静力学$4-2空间力偶系空间力偶及其矢量表示：400N400N空间力偶三要素：大小、1000N转向，力偶的作用面021所以空间力偶矩必须用0.5m量表示(b)(C)(a)图4-10力偶的平行移动m力偶的转向为右手螺旋法则。F空间力偶是一个自由矢量FY8

8 §4-2 空间力偶系 空间力偶三要素：大小、 转向，力偶的作用面 一、空间力偶及其矢量表示： 力偶的转向为右手螺旋法则。 空间力偶是一个自由矢量。 所以空间力偶矩必须用 矢量表示

静力学一、空间力偶的等效定理作用在同一刚体的两个力偶，若它们的力偶矩矢的相等，则两个力偶等效。由此可得出，空间力偶矩是自由矢量，它有三个要素：①力偶矩的大小=m②力偶矩的方向与力偶作用面法线方向相同③转向遵循右手螺旋规则。三、空间力偶系的合成与平衡nLm1、合成：m-m+m +...+m.1ilZw*=02、平衡： m=m,-0Zw=0投影式为：w=0O

9 二、空间力偶的等效定理 作用在同一刚体的两个力偶，若它们的力偶矩矢的相等，则 两个力偶等效。 由此可得出，空间力偶矩是自由矢量，它有三个要素： ①力偶矩的大小= ②力偶矩的方向——与力偶作用面法线方向相同 ③转向——遵循右手螺旋规则。 m 三、空间力偶系的合成与平衡 = = + + + = n i m m m mn mi 1 1、合成： 1 2  2、平衡： = =0 m mi 投影式为： mx =0 my =0 mz =0

静力学$·4-3力对点的矩与力对轴的矩一、力对点的矩的失量表示P3在平面：力对点的矩是代数量RP在空间：力对点的矩是矢量。[例］汽车反镜的球铰链B12-M. (F)大小：M。(F)=F·h=2ZAOB面积RTA(xy.z)量方位：作用面法线位置箭头指向：力矩转向（右手螺旋法则）图4-8力对点之矩10

10 在平面：力对点的矩是代数量。 在空间：力对点的矩是矢量。 [例] 汽车反镜的球铰链 §4-3 力对点的矩与力对轴的矩 一、力对点的矩的矢量表示 大小： MO (F) = F  h = 2AOB面积 矢量方位：作用面法线位置 箭头指向：力矩转向 （右手螺旋法则）