《工程力学》课程教学课件（PPT讲稿）第二篇 材料力学 第9章 弯曲变形

第9章弯曲变形

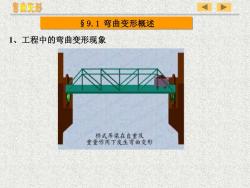
弯曲变形89.1弯曲变形概述1、工程中的弯曲变形现象力桥式吊梁在自重及重量作用下发生弯曲变形

§9.1 弯曲变形概述 1、工程中的弯曲变形现象

弯曲变形研究范围：等直梁在对称弯曲时位移的计算研究目的：①对梁作刚度校核；②解静不定梁（变形几何条件提供补充方程）

研究范围：等直梁在对称弯曲时位移的计算。 研究目的：①对梁作刚度校核； ②解静不定梁（变形几何条件提供补充方程）

弯曲变形2.弯曲变形的度量一一挠度和转角曲线方程：0转角w= w(x)1挠曲线挠度度w：截面形心W在y方向的位移xxw 向上为正转角θ：截面绕中性轴转过的角度。O 逆钟向为正由于小变形，截面形心在方向的位移忽略不计dv挠度转角关系为：～tano=dx

2.弯曲变形的度量——挠度和转角 挠曲线方程： w = w(x) 由于小变形，截面形心在x方向的位移忽略不计 挠度转角关系为： dx dw   tan = 挠曲线 y x x w 挠度  转角 挠度w：截面形心 在y方向的位移 w 向上为正 转角θ：截面绕中性轴转过的角度。  逆钟向为正

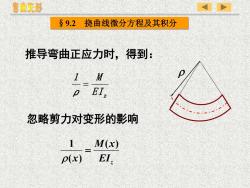
弯曲变形89.2挠曲线微分方程及其积分推导弯曲正应力时，得到：1MUpEI.忽略剪力对变形的影响1M(x)EL,p(x)

§9.2 挠曲线微分方程及其积分 推导弯曲正应力时，得到： E I z M ρ 1 = 忽略剪力对变形的影响 EIz M x x ( ) ( ) 1 =  

弯曲变形由数学知识可知：yld'yM(x) >0M(x) > 0dr??=+pdy1>0/1+dxx0略去高阶小量，得y4d'y1M(x)< 0M(x)<0dr?pd'y<0dx2X1d'yM(x)所以0dr?EL

由数学知识可知： 2 3 2 2 [1 ( ) ] 1 dx dy dx d y + =   略去高阶小量，得 2 2 1 dx d y =   所以 EIz M x dx d y ( ) 2 2  = 2 M(x) > 0 M(x) > 0 O d y dx 2 > 0 x y M(x) < 0 O dx d y 2 < 0 2 y x M(x) < 0

弯曲变形由弯矩的正负号规定可得，弯矩的符号与曲线的二阶导数符号一致，所以曲线的近似微分方程为：M(x)QMdr2EI由上式进行积分，就可以求出梁横截面的转角和挠度

由弯矩的正负号规定可得，弯矩的符号与挠曲 线的二阶导数符号一致，所以挠曲线的近似微分方 程为： EI z M x dx d w ( ) 2 2 = 由上式进行积分，就可以求出梁横截面的转角 和挠度

弯曲变形dwM(x)EIM(x)dxEL.dx积分一次得转角方程为：dwW= EI,0=[ M(x)dx +CEIdx再积分一次得挠度方程为：El, w= JJ M(x)dxd+ Cx+ D

EI z M x dx d w ( ) 2 2 = 积分一次得转角方程为：  = EI = M x dx +C dx dw EIz z  ( ) ( ) 2 2 M x dx d w EIz = 再积分一次得挠度方程为： EIz w =  M (x)dxdx+Cx + D

弯曲变形积分常数C、D由梁的位移边界条件和光滑连续条件确定。光滑连续条件位移边界条件AAAHAAA易w.=0WAL=WARW.=△WAL = WARw. =00 =0△一弹簧变形0 AL = 0AR

积分常数C、D 由梁的位移边界条件和光滑连续 条件确定。 A A A A A A ~ ~ ~ ~ ~ A A A A A A ~ ~ ~ ~ ~ A A A A A A ~ ~ ~ ~ ~ A A A A A A ~ ~ ~ ~ ~ A A A A A A ~ ~ ~ ~ ~ wA = 0 wA = 0  A = 0 wA =  位移边界条件 光滑连续条件 wAL = wAR  AL = AR wAL = wAR －弹簧变形

弯曲变形讨论：①适用于小变形情况下，、线弹性材料，细长构件的平面弯曲②可应用于求解承受各种载荷的等截面或变截面梁的位移。③积分常数由挠曲线变形的几何相容条件（边界条件、连续条件）确定。①优点：使用范围广，直接求出较精确；缺点：计算较繁

讨论： ①适用于小变形情况下、线弹性材料、细长构件的平面弯曲。 ②可应用于求解承受各种载荷的等截面或变截面梁的位移。 ③积分常数由挠曲线变形的几何相容条件（边界条件、连续 条件）确定。 ④优点：使用范围广，直接求出较精确； 缺点：计算较繁