内蒙古科技大学：《工程力学》课程授课教案（讲义）第10章 应力状态和强度理论

第10章教学方案-应力状态和强度理论应力状态概述二向应力状态分析的解析法基本内容三向应力状态强度理论概述四种常用的强度理论强度理论的应用了解应力状态分析的原因和一点应力状态的概念，掌握用微元描述一点应力状态。2、掌握平面应力状态中斜面上的正应力、切应力计算，熟练掌握教学目的主应力、主方向的确定及最大切应力的计算。了解广义胡克定律。了解强度理论的概念。5、掌握四种常用的强度理论，了解四种强度理论应用条件。重点一点应力状态的概念及描述；强度理论的概念及应用。难点

第 10 章 教学方案 ——应力状态和强度理论 基 本 内 容 应力状态概述 二向应力状态分析的解析法 三向应力状态 强度理论概述 四种常用的强度理论 强度理论的应用 教 学 目 的 1、了解应力状态分析的原因和一点应力状态的概念，掌握用微元 描述一点应力状态。 2、掌握平面应力状态中斜面上的正应力、切应力计算，熟练掌握 主应力、主方向的确定及最大切应力的计算。 3、了解广义胡克定律。 4、了解强度理论的概念。 5、掌握四种常用的强度理论 6、了解四种强度理论应用条件。 重 点 、 难 点 一点应力状态的概念及描述；强度理论的概念及应用

第10章应力状态和强度理论10.1应力状态概述10.1.1问题的提出工程中有许多构件，其危险截面上的危险点同时承受正应力和切应力，这种受力状态称为复杂应力状态。由于复杂应力状态变化繁多，在强度计算时不可能一二一通过实验确定失效时的极限应力。因此必须研究复杂应力状态的应力在各个方向的变化规律，为失效原因分析提供基础。10.1.2应力状态的概念受力构件内某一点处，各个不同方位截面上的应力及其关系称为一点的应力状态。为了研究一点的应力状态，可围绕该点取单元体。因为单元体的尺寸非常微小，可以认为各个面上的应力均匀分布相对的两个面上的应力情况完全相同。构件上一点的应力状态，可由围绕该点的单元体各面上的应力情况表示。换句话说，单元体的受力就代表该点的应力状态。10.1.3单元体的取法通常用应力已知的截面来截取单元体。例如在图10.1（a）所示的轴向拉伸构件中，为了分析 A点的应力状态，围绕A点用横截面和纵向截面截取出单元体研究，A点单元体受力如图所示。在图10.（b）所示的扭转圆轴中，为了分析表面上C点的应力状态，围绕C点用左右两个横截面、上下两个纵向截面和平行表面的一个纵向截面截取出单元体研究，C点单元体受力如图所示。在图10.1（c）所示的矩形截面悬臂梁上，若研究m-m截面上A、B、C三点的应力状态，围绕三点分别用横截面利纵向截面截取出单元体研究。横截面上的应力分布如图，大小可由弯曲应力计算公式确定。A点在梁横截面的最上端，横截面方向只受正应力作用，其单元体受力如图示：B点在中性轴上，横截面上只受切应力作用，根据该截面上剪力的方向，可确定切应力的方向如图，其单元体受力如图示：同理可确定C点的单元体受力如图示

第 10 章 应力状态和强度理论 10.1 应力状态概述 10.1.1 问题的提出 工程中有许多构件，其危险截面上的危险点同时承受正应力和切应力，这种受力状态称为复杂 应力状态。由于复杂应力状态变化繁多，在强度计算时不可能一一通过实验确定失效时的极限应力。 因此必须研究复杂应力状态的应力在各个方向的变化规律，为失效原因分析提供基础。 10.1.2 应力状态的概念 受力构件内某一点处，各个不同方位截面上的应力及其关系称为一点的应力状态。为了研究一点 的应力状态，可围绕该点取单元体。因为单元体的尺寸非常微小，可以认为各个面上的应力均匀分布， 相对的两个面上的应力情况完全相同。构件上一点的应力状态，可由围绕该点的单元体各面上的应力 情况表示。换句话说，单元体的受力就代表该点的应力状态。 10.1.3 单元体的取法 通常用应力已知的截面来截取单元体。例如在图 10.1（a）所示的轴向拉伸构件中，为了分析 A 点的应力状态，围绕 A 点用横截面和纵向截面截取出单元体研究，A 点单元体受力如图所示。在图 10.1 （b）所示的扭转圆轴中，为了分析表面上 C 点的应力状态，围绕 C 点用左右两个横截面、上下两个 纵向截面和平行表面的一个纵向截面截取出单元体研究，C 点单元体受力如图所示。在图 10.1（c） 所示的矩形截面悬臂梁上，若研究 m-m 截面上 A、B、C 三点的应力状态，围绕三点分别用横截面和 纵向截面截取出单元体研究。横截面上的应力分布如图，大小可由弯曲应力计算公式确定。A 点在梁 横截面的最上端，横截面方向只受正应力作用，其单元体受力如图示；B 点在中性轴上，横截面上只 受切应力作用，根据该截面上剪力的方向，可确定切应力的方向如图，其单元体受力如图示；同理可 确定 C 点的单元体受力如图示

0存司+H(a)自皇c中日图10.1取出单元体，确定其受力后，应用截面法和静力平衡条件就可求出单元体其它截面方向上的应力10.1.4主应力和主平面用绕构件内一点载取不同方向的单元体，则各个载面上的受力也各不相同。若某一截面上的无切应力，则称这种切应力为零的面为主平面。主平面上的正应力称为主应力。一般来说，受力构件的任意点上总存在三个互相垂直的主平面，也有三个主应力。三个主应力从大到小排列分别用01、02、03表示。若三个主应力中只有一个不等于零，称为单向应力状态，图10.1中的A点就是单向应力状态。若三个主应力中有两个不等于零，称为二向或平面应力状态，图10.1中的B、C点就是二向应力状态。若三个主应力都不等于零，称为三向或空间应力状态。单向应力状态也称为简单应力状态，二向和三向应力状态也统称为复杂应力状态10.2二向应力状态分析的解析法10.2.1二向应力状态下斜截面的应力向应力状态是最常见的一种应力情况。图10.2所示的单元体为二向应力状态的最一般的受力情况。建立图示坐标系，坐标轴、六、=分别是单元体三个互相垂直平面的法线，对应的面分别称为x面、y面、面，其上的应力加该面的名称作为下标，如o、，等。为了确定任意斜截面上的应力，需首先对单元体上的各应力正负号作如下约定：正应力：拉应力为正，压应力为负。切应力：使单元体顺时针旋转的切应力为正，反之为负。按照上述约定，图10.2中各应力6x、6和为正，ty为负。图10.2

取出单元体，确定其受力后，应用截面法和静力平衡条件就可求出单元体其它截面方向上的应力。 10.1.4 主应力和主平面 围绕构件内一点截取不同方向的单元体，则各个截面上的受力也各不相同。若某一截面上的无切 应力，则称这种切应力为零的面为主平面。主平面上的正应力称为主应力。一般来说，受力构件的任 意点上总存在三个互相垂直的主平面，也有三个主应力。三个主应力从大到小排列分别用 σ1、σ2、σ3 表示。若三个主应力中只有一个不等于零，称为单向应力状态，图 10.1 中的 A 点就是单向应力状态。 若三个主应力中有两个不等于零，称为二向或平面应力状态，图 10.1 中的 B、C 点就是二向应力状态。 若三个主应力都不等于零，称为三向或空间应力状态。单向应力状态也称为简单应力状态，二向和三 向应力状态也统称为复杂应力状态。 10.2 二向应力状态分析的解析法 10.2.1 二向应力状态下斜截面的应力 二向应力状态是最常见的一种应力情况。图 10.2 所示的单元体为二向应力状态的最一般的受力 情况。建立图示坐标系，坐标轴 x、y、z 分别是单元体三个互相垂直平面的法线，对应的面分别称为 x 面、y 面、z 面，其上的应力加该面的名称作为下标，如 σx、τy等。为了确定任意斜截面上的应力， 需首先对单元体上的各应力正负号作如下约定： ⚫ 正应力：拉应力为正，压应力为负。 ⚫ 切应力：使单元体顺时针旋转的切应力为正，反之为负。 按照上述约定，图 10.2 中各应力 σx、σy和 τx为正，τy为负。 图 10.1 图 10.2

用垂直于=面、与x面夹角为α的斜截面将单元体假想地截开，如图10.3（a）。由于所有应力作用线均平行于，平面，将单元体受力图投影简化为图10.3（b）形式，x、y面和斜截面用投影的线段表示。取出楔形体 ABC 研究，斜截面上的应力 ca、ta按正向假设标出，如图 10.3（c）所示。若设斜截面的面积为dA，则侧面 AB和底面AC 的面积分别为dAcosα 和dAsinα。则楔形体ABC 的受力图如图10.3（d）所示。列斜截面法向n和切向t的投影平衡方程，有图10.3ZF,=0, a dA-(o, dAcosa)cosα+(t, dAcosa)sin α-(c, d Asin α)sin α+(t, d Asin α)cosα= CZF, =0, tadA-(o, dAcosa)sin α-(t, dAcosa)cosα+(c, d Asin a)sα+(t,dAsin α)sin 注意到和，数值上相等，都用表示，利用三角公式，上面两式简化为a,+a,0-0cin20(10-1)(10-2)2α+t,cos2a以上公式就是计算二向应力状态下任意斜截面上应力的公式。这里α是指斜截面与×截面的夹角，即两截面外法线正向 x和 n 间的夹角。规定由x 轴正向转到法线n 正向，若为逆时针转向，α为正顺时针转向，α为负。在应用以上公式时，应注意正确地选取各量的符号。还应注意到，公式中的斜截面仅是指垂直于：面的斜截面，并不能求解任意斜截面上的应力。10.2.2主应力和主平面方位斜截面上的应力是随α角的改变而变化的。利用以上公式就可进一步确定正应力和切应力的极值和所在位置

用垂直于 z 面、与 x 面夹角为 α 的斜截面将单元体假想地截开，如图 10.3（a）。由于所有应力 作用线均平行于 z 平面，将单元体受力图投影简化为图 10.3（b）形式，x、y 面和斜截面用投影的线 段表示。取出楔形体 ABC 研究，斜截面上的应力 σα、τα按正向假设标出，如图 10.3（c）所示。若设 斜截面的面积为 dA，则侧面 AB 和底面 AC 的面积分别为 dAcosα 和 dAsinα。则楔形体 ABC 的受力图 如图 10.3（d）所示。 列斜截面法向 n 和切向 t 的投影平衡方程，有 ( d sin ) cos ( d sin )sin 0 0, d ( d cos )sin ( d cos ) cos ( d sin )sin ( d sin ) cos 0 0, d ( d cos ) cos ( d cos )sin + + = = − − − + = = − +                               A A F A A A A A F A A A y y t x x y y n x x 注意到 τx和 τy数值上相等，都用 τx表示，利用三角公式，上面两式简化为          cos 2 sin 2 2 2 x x y x y − − + + = （10-1）        sin 2 cos 2 2 x x y + − = （10-2） 以上公式就是计算二向应力状态下任意斜截面上应力的公式。这里 α 是指斜截面与 x 截面的夹角， 即两截面外法线正向 x 和 n 间的夹角。规定由 x 轴正向转到法线 n 正向，若为逆时针转向，α 为正； 顺时针转向，α 为负。在应用以上公式时，应注意正确地选取各量的符号。还应注意到，公式中的斜 截面仅是指垂直于 z 面的斜截面，并不能求解任意斜截面上的应力。 10.2.2 主应力和主平面方位 斜截面上的应力是随 α 角的改变而变化的。利用以上公式就可进一步确定正应力和切应力的极值 和所在位置。 图 10.3

将公式（10-1）对α求导数并令其为零，得o-doa=sin 2α+T, cos2α|-=0da2与（10-2）式比较，可见在正应力的极值作用截面上，切应力为零。根据主应力和主平面的定义，正应力的极值就是主应力，其作用面就是主平面。以表示主平面方位，则由上式解得主平面方位2ttan 2αg =(10-3)0-0从上式可求出相差90°的两个角。加上主平面：面，构成互相垂直的三个主平面，形成由主平面组成的主应力单元体。由（10-3）式求出 sin2ao和cos2ao，代入（10-1）式，得主应力为o.-0. +:Om/o,+o,+(10-4)amia10.2.3最大切应力将公式（10-2）对α求导数并令其为零，解得切应力的极值作用平面方位（用α表示）为0.-0tan 2α,(10-5)2T从上式也可求出相差90°的两个αi角。比较（10-3）式与（10-5）式可得αj=αg± 450即切应力的极值作用平面与主平面成45°角。由（10-5）式求出sin2αi和cos2αi，代入（10-2）式，得切应力的最大和最小值为(10-6)=+TminJ【例10-1】单元体受力如图10.4（a）所示（应力单位：MPa)。试求：（1）指定斜截面上的应力；（2）主应力和主平面方位：（3）最大切应力(a)（b)图10.4解：（1）计算斜截面的应力建立图10.4（a）所示坐标轴，根据符号规定有：0f=60=600将上述数据代入（10-1）和（10-2）式，可得_60-80,60±80cos120 35sin 120° =-75.3MPa0.600L

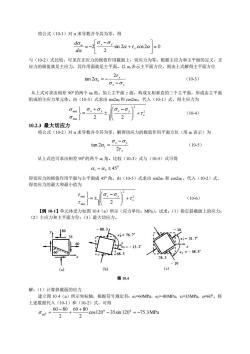
将公式（10-1）对 α 求导数并令其为零，得 sin 2 cos 2 0 2 2  =      + − = −         x x y d d 与（10-2）式比较，可见在正应力的极值作用截面上，切应力为零。根据主应力和主平面的定义，正 应力的极值就是主应力，其作用面就是主平面。以 α0 表示主平面方位，则由上式解得主平面方位 x y x     − = − 2 tan 2 0 （10-3） 从上式可求出相差 900 的两个 α0 角。加上主平面 z 面，构成互相垂直的三个主平面，形成由主平面 组成的主应力单元体。由（10-3）式求出 sin2α0 和 cos2α0，代入（10-1）式，得主应力为 2 2 min max 2 2 x x y x y        +         −  + =    （10-4） 10.2.3 最大切应力 将公式（10-2）对 α 求导数并令其为零，解得切应力的极值作用平面方位（用 α1 表示）为 x x y     2 tan 2 1 − = （10-5） 从上式也可求出相差 900 的两个 α1 角。比较（10-3）式与（10-5）式可得 0 1 =  0  45 即切应力的极值作用平面与主平面成 450 角。由（10-5）式求出 sin2α1 和 cos2α1，代入（10-2）式， 得切应力的最大和最小值为 2 2 min max 2 x x y      +         − =     （10-6） 【例 10-1】单元体受力如图 10.4（a）所示（应力单位：MPa）。试求：（1）指定斜截面上的应力； （2）主应力和主平面方位；（3）最大切应力。 解：（1）计算斜截面的应力 建立图 10.4（a）所示坐标轴，根据符号规定有：σx=60MPa，σy=-80MPa，τx=35MPa，α=600。将 上述数据代入（10-1）和（10-2）式，可得 cos120 35sin 120 75.3MPa 2 60 80 2 60 80 0 0 6 00 − = − + + −  = 图 10.4

+2+35co20=43MT.600（2）计算主应力和主平面方位由（10-3）式得2×35=0.5tan 2αg =-60+80解得α =-13.3°, α% = 76.70为了确定对应主平面上的主应力值，分别将α和α值代入（10-1）式，得0 0 0 0 0-26)-35s-260) -83 a_ 0-80 0 0o0134 - 3sn134 83 MaG=若按主应力排列，则,=68.3MPa,，=0,，=-88.3MPa。主应力单元体如图10.4（b）所示。（3）最大切应力由（10-6）式得[60+80 +35* =±78.3MPa2n其作用面方位由α,α%±45°得：α=31.7°和α=-58.3%。其单元体如图10.4（c）所示。10.4三向应力状态10.4.1三向应力状态概述三向应力状态是最一般的应力状态情况，其单元体受力为：在每个截面上都有正应力和平行于该截面棱边的两个切应力分量，如图10.8（a）所示。理论分析证明，与二向应力状态类似，三向应力状态单元体也可以找到互相垂直的三个主平面，得到主应力单元体，如图10.8（b）所示在工程实际中经常会出现三向应力状态的情况。例如滚珠轴承中的滚珠与外圈的接触处，由于有接触应力3的作用，单元体会向四周膨胀，引起周围材料对它的约束应力o1和o2，受力呈三向应力状态，如图10.9所示

sin 120 35cos120 43.1MPa 2 60 80 0 0 600 + = +  = （2）计算主应力和主平面方位 由（10-3）式得 0.5 60 80 2 35 tan 2 0 = − +   = − 解得 0 0 0  0 = −13.3 ,  = 76.7 为了确定对应主平面上的主应力值，分别将  0 和  0  值代入（10-1）式，得 cos( 26.6 ) 35sin( 26.6 ) 68.3MPa 2 60 80 2 60 80 0 0 0 − − − = + + −   = cos153.4 35sin 153.4 88.3MPa 2 60 80 2 60 80 0 0 0 − = − + + −   = 若按主应力排列，则 68.3MPa , 0 , 88.3MPa  1 =  2 =  3 = − 。主应力单元体如图 10.4（b）所示。 （3）最大切应力 由（10-6）式得 35 78.3MPa 2 60 80 2 2 min max  + =       + =       其作用面方位由 0 1 =  0  45 得： 0 1 = 31.7 和 0 1  = −58.3 。其单元体如图 10.4（c）所示。 10.4 三向应力状态 10.4.1 三向应力状态概述 三向应力状态是最一般的应力状态情况，其单元体受力为：在每个截面上都有正应力和平行于 该截面棱边的两个切应力分量，如图 10.8（a）所示。理论分析证明，与二向应力状态类似，三向应 力状态单元体也可以找到互相垂直的三个主平面，得到主应力单元体，如图 10.8（b）所示。 在工程实际中经常会出现三向应力状态的情况。例如滚珠轴承中的滚珠与外圈的接触处，由于 有接触应力 σ3 的作用，单元体会向四周膨胀，引起周围材料对它的约束应力 σ1 和 σ2，受力呈三向应 力状态，如图 10.9 所示

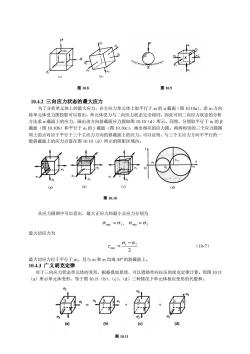
图10.8图10.910.4.2三向应力状态的最大应力为了分析单元体上的最大应力，在主应力单元体上取平行于的α截面（图10.10a)，沿方向将单元体受力图投影可以看出，单元体受力与二向应力状态完全相同，因此可用二向应力状态的分析方法求α截面上的应力，画出该方向斜截面应力圆如图10.10（d）所示。同理，分别取平行于α1的β截面（图10.10b）和平行于o2的截面（图10.10c），画出相应的应力圆。两两相切的三个应力圆圆周上的点对应于平行于三个主应力方向的斜截面上的应力。可以证明，与三个主应力方向不平行的一般斜截面上的应力点落在图10.10（d）所示的阴影区域内。#(b)(d)e图10.10从应力圆图中可以看出，最大正应力和最小正应力分别为Omx =01, Cmin =0,最大切应力为mx = C -0(10-7)2最大切应力位于平行于o2，且与o和均成45°的斜截面上。10.4.3广义胡克定律对于三向应力状态单元体的变形，根据叠加原理，可以借助单向拉压的虎克定律计算。即图10.11(a）所示单元体变形，等于图10.11（b）、（c)、（d）三种情况下单元体相应变形的代数和。/i1+F-(b)al(c)(d)图 10.11

图 10.11 10.4.2 三向应力状态的最大应力 为了分析单元体上的最大应力，在主应力单元体上取平行于 σ3 的 α 截面（图 10.10a），沿 σ3 方向 将单元体受力图投影可以看出，单元体受力与二向应力状态完全相同，因此可用二向应力状态的分析 方法求 α 截面上的应力，画出该方向斜截面应力圆如图 10.10（d）所示。同理，分别取平行于 σ1 的 β 截面（图 10.10b）和平行于 σ2 的 γ 截面（图 10.10c），画出相应的应力圆。两两相切的三个应力圆圆 周上的点对应于平行于三个主应力方向的斜截面上的应力。可以证明，与三个主应力方向不平行的一 般斜截面上的应力点落在图 10.10（d）所示的阴影区域内。 从应力圆图中可以看出，最大正应力和最小正应力分别为 max 1 min 3  =  ,  =  最大切应力为 2 1 3 max    − = （10-7） 最大切应力位于平行于 σ2，且与 σ1 和 σ3 均成 450 的斜截面上。 10.4.3 广义胡克定律 对于三向应力状态单元体的变形，根据叠加原理，可以借助单向拉压的虎克定律计算。即图 10.11 （a）所示单元体变形，等于图 10.11（b）、（c）、（d）三种情况下单元体相应变形的代数和。 图 10.10 图 10.8 图 10.9

当只有ai作用时（图10.11b），棱边1将伸长，棱边2、3将缩短。各方向的应变为-,6=8--同理，在只有2作用（图10.11c）和只有作用时（图10.11d)，各方向的应变分别为-%, 0/-6--%6-,0-1--g在小变形条件下，叠加可得三个主应力同时作用时各棱边的应变为5) =[0, - (02 +0,)]62 =[02 -M(o +0)](10-8)6, =(0, -4(0, +0,)上式称为广义虎克定律。所求的应变c1、62、c3称为主应变，其中ei是所有方向应变中的最大值，即Cml=6对于线弹性小变形条件下的各向同性材料，正应变只与正应力有关，与切应力无关。因此，对于如图10.8（a）所示的一般受力情况单元体，其广义虎克定律可表示为o. -u(o, +0.)]6.=(10-9),-μ(o,+o.)6=-μ(ox +o,)【例10-4】图10.12所示一个宽、深均为10mm的刚性槽内放置一10×10×10（单位：mm）的正立方体钢块，顶部施加均布压力p=60MPa，钢材料的弹性模量E=200GPa，泊松比μ=0.3。假设钢块与槽之间光滑接触。求钢块的三个主应力和最大切应力解：（1）计算钢块三个方向的应力选取图示坐标系，沿方向作用均布压力，则0y=-p=-60MPa 沿：方向不受力，且变形不受限制，则6:=0沿x方向受刚性槽约束不变形，则 c=0根据广义虎克定律g,-μ(, +o.)]=0图 10.12解得 0=-18MPa（2）确定钢块的主应力

当只有 σ1 作用时（图 10.11b），棱边 1 将伸长，棱边 2、3 将缩短。各方向的应变为 E E 1 2 3 1 1 ,        =  =  = − 同理，在只有 σ2 作用（图 10.11c）和只有 σ3 作用时（图 10.11d），各方向的应变分别为 E E E E 3 1 2 3 3 2 1 3 2 2 , ,             = =  = −  =  =  = − 在小变形条件下，叠加可得三个主应力同时作用时各棱边的应变为                = − + = − + = − + ( ) 1 ( ) 1 ( ) 1 3 3 1 2 2 2 1 3 1 1 2 3                E E E （10-8） 上式称为广义虎克定律。所求的应变 ε1、ε2、ε3 称为主应变，其中 ε1 是所有方向应变中的最大值，即 max 1  =  对于线弹性小变形条件下的各向同性材料，正应变只与正应力有关，与切应力无关。因此，对于 如图 10.8（a）所示的一般受力情况单元体，其广义虎克定律可表示为                = − + = − + = − + ( ) 1 ( ) 1 ( ) 1 z z x y y y x z x x y z E E E                （10-9） 【例 10-4】 图 10.12 所示一个宽、深均为 10mm 的刚性槽内放置一 10×10×10（单位：mm）的 正立方体钢块，顶部施加均布压力 p=60MPa，钢材料的弹性模量 E=200GPa，泊松比 μ=0.3。假设钢 块与槽之间光滑接触。求钢块的三个主应力和最大切应力。 解：（1）计算钢块三个方向的应力 选取图示坐标系，沿 y 方向作用均布压力，则 σy= –p= –60MPa 沿 z 方向不受力，且变形不受限制，则 σz=0 沿 x 方向受刚性槽约束不变形，则 εx=0 根据广义虎克定律  ( ) 0 1 x = x − y + z = E      解得 σx= –18MPa （2）确定钢块的主应力 图 10.12

将o、0y、6.从大到小排列，三个主应力为01=0,02-18MPa，3=-60Mp（3）计算钢块的最大切应力91-0=30MPa10.3强度理论概述10.5.1材料的破坏形式一些材料的破坏现象。例如，低碳钢在拉伸时，当应力达到屈服极限时，产生明显前面曾接触过的塑性变形，丧失了承载能力；并且可以观察到在45°斜截面方向出现滑移线的破坏现象；铸铁在拉伸时，当应力达到强度极限时，会发生断裂破坏，断口位置在横截面方向。总结材料在各种受力情况下的破坏形式可以归纳为两种：材料在未产生明显的塑性变形情况下突然断裂的破坏形式，称为脆性断裂：材料产生明显的塑性变形、丧失了承载能力的破坏形式，称为塑性屈服。通常情况下，脆性材料的破坏形式是脆性断裂；塑性材料的破坏形式是塑性屈服。但实验也表明，应力状态也对材料的破坏形式有影响，例如，在三向拉伸应力状态下，即使是塑性材料也会发生脆性断裂：：在三向压缩应力状态下，即使是脆性材料也会发生塑性屈服。10.5.2强度理论的概念在材料处于单向应力状态和纯剪切应力状态时，其破坏条件和强度条件可以完全建立在实验的基础上。然而，工程中许多构件的危险点处于复杂应力状态，由于复杂应力状态单元体的三个主应力可以有无数种组合，想要通过实验来建立强度条件是不可能的，只能寻求新的方法，来建立复杂应力状态下的强度条件。此外，虽然通过实验已经建立了基本变形下的强度条件，但对引起材料破坏的原因还缺乏了解，也需要加以研究。通过长期的观察、实验和分析，人们提出了许多解释在复杂应力状态下材料强度破坏原因的假说。这些经过科学实验和工程实际检验，得到普遍认同的假说称为强度理论。这些假说认为不论在何种应力状态下，当同样的因素达到同一极限值时，材料就会发生破环。按照这些假说，可以用单向拉伸时的实验结果确定破坏因素的极限值，从而建立复杂应力状态下的强度条件由于材料的多样性和应力状态的复杂性，一种强度理论经常是适合这类材料却不适合另一类材料，适合一般应力状态却不适合特殊应力状态，所以现有的强度理论还并不能解决所有的强度问题。强度理论的研究必将随着材料科学和工程技术的不断进步而得到发展。10.4四种常用的强度理论10.6.1最大拉应力理论（第一强度理论）认为：最大拉应力是引起材料发生脆性断裂的主要因素。破坏条件：按照这一理论，不论材料处于何种应力状态，只要最大拉应力i达到某一极限值。就会发生脆性断裂。在单向拉伸应力状态下，当最大拉应力αi达到材料的强度极限ob时，发生脆性断裂，因此极限应力ou就是强度极限ob。所以材料的破坏条件为g, =0u=0)强度条件：将极限应力除以安全因数得到许用应力[0]，则最大拉应力理论的强度条件为a, ≤[0] (10-10)

将 σx、σy、σz 从大到小排列，三个主应力为 σ1=0，σ2= –18MPa，σ3= –60Mpa （3）计算钢块的最大切应力 30MPa 2 1 3 max = − =    10.3 强度理论概述 10.5.1 材料的破坏形式 前面曾接触过一些材料的破坏现象。例如，低碳钢在拉伸时，当应力达到屈服极限时，产生明显 的塑性变形，丧失了承载能力；并且可以观察到在 450 斜截面方向出现滑移线的破坏现象；铸铁在拉 伸时，当应力达到强度极限时，会发生断裂破坏，断口位置在横截面方向。总结材料在各种受力情况 下的破坏形式可以归纳为两种：材料在未产生明显的塑性变形情况下突然断裂的破坏形式，称为脆性 断裂；材料产生明显的塑性变形、丧失了承载能力的破坏形式，称为塑性屈服。 通常情况下，脆性材料的破坏形式是脆性断裂；塑性材料的破坏形式是塑性屈服。但实验也表明， 应力状态也对材料的破坏形式有影响，例如，在三向拉伸应力状态下，即使是塑性材料也会发生脆性 断裂；在三向压缩应力状态下，即使是脆性材料也会发生塑性屈服。 10.5.2 强度理论的概念 在材料处于单向应力状态和纯剪切应力状态时，其破坏条件和强度条件可以完全建立在实验的基 础上。然而，工程中许多构件的危险点处于复杂应力状态，由于复杂应力状态单元体的三个主应力可 以有无数种组合，想要通过实验来建立强度条件是不可能的，只能寻求新的方法，来建立复杂应力状 态下的强度条件。此外，虽然通过实验已经建立了基本变形下的强度条件，但对引起材料破坏的原因 还缺乏了解，也需要加以研究。 通过长期的观察、实验和分析，人们提出了许多解释在复杂应力状态下材料强度破坏原因的假说。 这些经过科学实验和工程实际检验，得到普遍认同的假说称为强度理论。 这些假说认为不论在何种应力状态下，当同样的因素达到同一极限值时，材料就会发生破坏。按 照这些假说，可以用单向拉伸时的实验结果确定破坏因素的极限值，从而建立复杂应力状态下的强度 条件。 由于材料的多样性和应力状态的复杂性，一种强度理论经常是适合这类材料却不适合另一类材 料，适合一般应力状态却不适合特殊应力状态，所以现有的强度理论还并不能解决所有的强度问题。 强度理论的研究必将随着材料科学和工程技术的不断进步而得到发展。 10.4 四种常用的强度理论 10.6.1 最大拉应力理论（第一强度理论） 认为：最大拉应力是引起材料发生脆性断裂的主要因素。 破坏条件：按照这一理论，不论材料处于何种应力状态，只要最大拉应力 σ1 达到某一极限值 σu， 就会发生脆性断裂。在单向拉伸应力状态下，当最大拉应力 σ1 达到材料的强度极限 σb 时，发生脆性 断裂，因此极限应力 σu 就是强度极限 σb。所以材料的破坏条件为  1 =  u =  b 强度条件：将极限应力除以安全因数得到许用应力[σ]，则最大拉应力理论的强度条件为    1 （10-10）

应用：这一理论能较好地解释均质脆性材料如砖石、玻璃、铸铁等的破坏现象，与实验结果较咳合，得到广泛应用。但该理论未考虑另外两个主应力的影响，对不存在拉应力的受力情况也不适用最大拉应力理论在17世纪由伽里略提出，是最早的强度理论，故也称为第一强度理论。10.6.2最大拉应变理论（第二强度理论）认为：最大拉应变是引起材料发生脆性断裂的主要因素。破坏条件：按照这一理论，不论材料处于何种应力状态，只要最大拉应变ei达到某一极限值ea就会发生脆性断裂。在单向拉伸应力状态下，当最大拉应力αi达到材料的强度极限ob时，最大拉应变达到极限值s。=°%E。所以材料的破坏条件为5,=6, =%以主应力表达为0-μ(02 +03)=0强度条件：将极限应力除以安全因数得到许用应力[0]，则最大拉应变理论的强度条件为01 -μ(0, +0,)≤[0](10-11)应用：这一理论能较好地解释石料和混凝土等脆性材料受轴向压缩时沿纵向截面开裂的破坏现象。但该理论与许多实验结果不相吻合，所以目前应用较少最大拉应变理论在17世纪后期由马里奥特提出，也称为第二强度理论。10.6.3最大切应力理论（第三强度理论）认为：最大切应力是引起材料发生塑性届服的主要因素。破坏条件：按照这一理论，不论材料处于何种应力状态，只要最大切应力tmax达到某一极限值 tu，就会发生塑性屈服。在单向拉伸应力状态下，当最大拉应力达到材料的屈服极限时，发生屈服破坏，此时在45°斜截面上最大切应力达到极限值，即有t=0s/2。所以材料的破坏条件为Tm=T,-%以主应力表达为0,-0, =0,强度条件：将极限应力6,除以安全因数得到许用应力[o]，则最大切应力理论的强度条件为0, -0, ≤[0](10-12)应用：这一理论较圆满地解释了塑性材料的屈服破坏现象，与许多塑性材料发生屈服的实验结果相吻合，得到广泛应用。但该理论未考虑中间主应力の2的影响，在二向应力状态下，理论计算结果与实验比较偏安全。最大切应力理论由库伦提出，后经屈雷斯卡加以完善，也称为第三强度理论。10.6.4畸变能密度理论（第四强度理论）畸变能密度概念：在弹性范围内，变形固体在外力作用下会发生弹性变形。外力作用点产生位移，则外力对变形固体作功。根据能量守恒原理，外力的功转化为了一种能量，储存在了变形固体内。这种能量称为应变能。在外力撤除后变形固体释放应变能使变形完全恢复。因为变形固体内各点的变形可能不同，为了衡量各点的应变能的大小，用单位体积内储存的应变能来表示，称为应变能密度。单元体内储存的应变能多少用单元体的应变能密度表示。单元体的变形形式包含体积改变和形状改变两种，因此，单元体的应变能密度也包括由体积改变产生的体积改变能密度和由形状改变产生的畸变能

应用：这一理论能较好地解释均质脆性材料如砖石、玻璃、铸铁等的破坏现象，与实验结果较吻 合，得到广泛应用。但该理论未考虑另外两个主应力的影响，对不存在拉应力的受力情况也不适用。 最大拉应力理论在 17 世纪由伽里略提出，是最早的强度理论，故也称为第一强度理论。 10.6.2 最大拉应变理论（第二强度理论） 认为：最大拉应变是引起材料发生脆性断裂的主要因素。 破坏条件：按照这一理论，不论材料处于何种应力状态，只要最大拉应变 ε1 达到某一极限值 εu， 就会发生脆性断裂。在单向拉伸应力状态下，当最大拉应力 σ1 达到材料的强度极限 σb 时，最大拉应 变达到极限值 E b u   = 。所以材料的破坏条件为 E b 1 u   =  = 以主应力表达为 1 2 3 b  − ( + ) =  强度条件：将极限应力除以安全因数得到许用应力[σ]，则最大拉应变理论的强度条件为  − ( + )   1 2 3 （10-11） 应用：这一理论能较好地解释石料和混凝土等脆性材料受轴向压缩时沿纵向截面开裂的破坏现 象。但该理论与许多实验结果不相吻合，所以目前应用较少。 最大拉应变理论在 17 世纪后期由马里奥特提出，也称为第二强度理论。 10.6.3 最大切应力理论（第三强度理论） 认为：最大切应力是引起材料发生塑性屈服的主要因素。 破坏条件：按照这一理论，不论材料处于何种应力状态，只要最大切应力 τmax 达到某一极限值 τu， 就会发生塑性屈服。在单向拉伸应力状态下，当最大拉应力达到材料的屈服极限 σs 时，发生屈服破 坏，此时在 450 斜截面上最大切应力达到极限值，即有 τu=σs/2。所以材料的破坏条件为 2 s max u   =  = 以主应力表达为  1 − 3 =  s 强度条件：将极限应力 σs 除以安全因数得到许用应力[σ]，则最大切应力理论的强度条件为  −   1 3 （10-12） 应用：这一理论较圆满地解释了塑性材料的屈服破坏现象，与许多塑性材料发生屈服的实验结果 相吻合，得到广泛应用。但该理论未考虑中间主应力 σ2 的影响，在二向应力状态下，理论计算结果 与实验比较偏安全。 最大切应力理论由库伦提出，后经屈雷斯卡加以完善，也称为第三强度理论。 10.6.4 畸变能密度理论（第四强度理论） 畸变能密度概念：在弹性范围内，变形固体在外力作用下会发生弹性变形。外力作用点产生位移， 则外力对变形固体作功。根据能量守恒原理，外力的功转化为了一种能量，储存在了变形固体内。这 种能量称为应变能。在外力撤除后变形固体释放应变能使变形完全恢复。因为变形固体内各点的变形 可能不同，为了衡量各点的应变能的大小，用单位体积内储存的应变能来表示，称为应变能密度。单 元体内储存的应变能多少用单元体的应变能密度表示。单元体的变形形式包含体积改变和形状改变两 种，因此，单元体的应变能密度也包括由体积改变产生的体积改变能密度和由形状改变产生的畸变能