《电路》课程教学资源（课后课件）有例题_第8章 相量法

思考：一阶电路中，激励不是恒定直流，而是正弦电压，响应如何求解？Rtz0+例：RL串联电路，-0时开关SUR+X闭合，u=Umcos(ot+Φu),A26求开关阴合厨i0-？资料！解：由KVL得di+ Rii= Umcos(ot+ Φu)dt其通解为：i=i'+i"请勿其中i'为其特解，i"为其对应的齐次微分方程通解。公

SDUT 内 部 资 料！ 请 勿 外 传！ 思考：一阶电路中，激励不是恒定直流，而是正弦电 压，响应如何求解？ 例：RL串联电路，t=0时开关 闭合 ，us =Umcos(wt+u )， 求开关闭合后，i(t)=? t≥0+ us + - + -uL R L i + uR - L diL dt + RiL= Umcos(wt+  u ) 其通解为： iL= iL '+ iL '' 解：由KVL得 其中 iL ' 为其特解， iL ''为其对应的齐次微分方程通解

Rt≥0.OORi= Umcos(ot $.)UR+us其通解为：i=i+i'R(1)先求特解iu,=Umcos(at+du)特解的形式：i=Imcos(ot+の)di'+ Rin Un数(a+ 0.)则dt-のLImsin(ot+)+RImcos(ot+0) =Umcos(ot+ Φu)整理得Im[R cos(αt + 0) - oL sin(at+ )] = U m cos(ot + d.)勿外传！

SDUT 内 部 资 料！ 请 勿 外 传！ dt us =Umcos(wt+u ) L R t = t≥0+ us + - + -uL R L i + uR - (1)先求特解iL ' 特解的形式：i' L= Imcos(wt +q ) -wLImsin(wt+q ) +RImcos(wt+q ) =Umcos(wt+  u ) 则 L di' L + Ri' L = Umcos(wt+  u ) [ cos( ) sin( )] cos( ) m w +q -w w +q = w + u I R t L t U t m 整理得 L diL dt + RiL= Umcos(wt+  u ) 其通解为： iL= iL '+ iL

Im[R cos(αt + O) - oL sin(ot + 0)] = Um cos(ot + d.)SDUTaLI. :R?+(oL)[cos(ot + 0)sin(ot + O)) = U cos(ot + d.R2 +(oL)R2 + (oL)I m ' R? + (oL)lcos @ cos(ot + 0)-sin p sin(αot +O)) = U m cos(ot + d.)部Rcos(ot+0+Φ)其中cos=令Z|= /R2 +(oL)2““料！R* +(oL)?aL则Im zcos(ot + 0 + p) = Um cos(ot + d.)sin@=/R? +(oL)2Imz|=Um， +=d.Ur因此特解：it=Imcos(at +ocos(at + Φu-Φ)玄外传！

SDUT 内 部 资 料！ 请 勿 外 传！ [ cos( ) sin( )] cos( ) m w +q -w w +q = w +  u I R t L t U t m sin( )] cos( ) ( ) cos( ) ( ) ( ) [ u 2 2 2 2 2 2 m w q w  w w w q w w + = + + + - +  + t U t R L L t R L R I R L m ( ) [cos cos( ) sin sin( )] cos( ) u 2 2 Im  R + wL  wt +q -  wt +q = Um wt + cos(wt+q +) 2 2 2 2 ( ) sin , ( ) cos R L L R L R w w  w  + = + 2 2 其中 = 令Z = R + (wL) cos( ) cos( ) m w +q + = w + u I  Z t U t 则 m m = q + =  u I  Z U m ， |Z| Um 因此特解：i' L = Imcos(wt +q ) = cos(wt +  u-)

Um特解：ii=Imcos(ot +の)=cos(t + Φu-p)[2oTAe-!·再求通解iUmT.cos(ot+ Φu-p)+ A ei=i+i"R[Z]OOUR由i(0+)0定出;+++部资1usuiUmL类则cos(Φu-Φ)T=A=R[2]UUmmcos(u-) e-cos(ot+ Φu-P)LL=UR=RiL[Z][Zdi,ui=L暂态分量"随时稳态分量讠是与外加dt间的增长衰臧为零。激励同频率的正弦量外传！

SDUT 内 部 资 料！ 请 勿 外 传！ |Z| Um 特解：i' L = Imcos(wt +q ) = cos(wt +  u-) |Z| Um iL = cos(wt+  u-)+ A e - t t 由iL (0+ ) = 0定出： A = - |Z| Um cos( u-) |Z| Um iL = cos(wt+  u-)- cos( u-) e |Z| Um - t t 稳态分量i‘ L是与外加 激励同频率的正弦量 暂态分量i" L随时 间的增长衰减为零。 l再求通解iL '' iL '+ iL '' = A e - t t L R t = us + - + -uL R L i + uR - uR = R iL uL= L diL dt 则

第8章相量法SDUT本章目录K立8.1复数8.2正弦量8.3相量法的基础8.4电路定律的相量形式传！

SDUT 内 部 资 料！ 请 勿 外 传！ 第8章 相量法 8.1 复数 8.2 正弦量 8.3 相量法的基础 8.4 电路定律的相量形式 本章目录

重点口1.复数的表示形式、相互转换和加减乘除运算：口2.正弦量和相量之间的关系，相位差和有效值等基本概念;口3.单一无件的交流电路（电压和电流的关系）；相量表示法？资料！准备一个科学计算器！！！与其它章节的联系是学习第9、10、11、有2章的基础。必须熟练掌握相量法的解析运算。传！

SDUT 内 部 资 料！ 请 勿 外 传！ 重点 p 1.复数的表示形式、相互转换和加减乘除运算； p 2.正弦量和相量之间的关系，相位差和有效值等 基本概念； p 3.单一元件的交流电路（电压和电流的关系）； 相量表示法； 是学习第 9、10、11、12章的基础。  与其它章节的联系 必须熟练掌握相量法的解析运算。 准备一个科学 计算器！！！

例：电路如图所示单相正弦交流电路中，已知交流电压表V1的读数为60V，V2的读数为160V，求V的读数。A.60B.160R鄂C.220资D.以上都不对请勿外2提交答案！

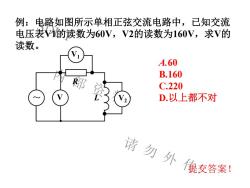
SDUT 内 部 资 料！ 请 勿 外 传！ 例：电路如图所示单相正弦交流电路中，已知交流 电压表V1的读数为60V，V2的读数为160V，求V的 读数。 R L V1 ～ V V2 提交答案！ A.60 B.160 C.220 D.以上都不对

$8-1 复数复数A可用复平面上的有向线段来表示。该有向线段的长度「A称为复数A的模，该有向线段与实轴正方向的夹角θ称为复数A的辐角Ae资料6A=a+jb复数F的实部a及虚部b与模及辐角的关系为：+ja =Acos0,[A| = Va? +b?Ab请bb =A sin 0,A=arctan--0+1a传！a

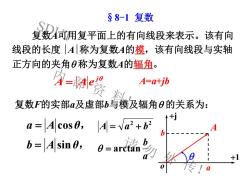
SDUT 内 部 资 料！ 请 勿 外 传！ §8-1 复数 复数A可用复平面上的有向线段来表示。该有向 线段的长度 |A|称为复数A的 ，该有向线段与实轴 正方向的夹角q 称为复数A的 。 ， ， b A θ a A θ sin cos = = a b A a b arctan 2 2 = = + q A=a+jb jq A = Ae 复数F的实部a及虚部b与模及辐角q 的关系为： o +j +1 A a q b

1.复数的表示形式(4)极坐标形式(1)代数形式A=a+jbA=A|Z0Re[A]=a,Im[A]=b+j(2)指数形式韶资料AhA=|A|ej ,其中ejo=cos0+jsin00+11(3)三角形式0aA=| A I(coso+ jsin)清勿=Va?-Th外a= A|cos0, b=A|sin0bA =arctanha

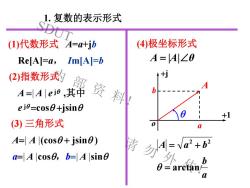
SDUT 内 部 资 料！ 请 勿 外 传！ 1. 复数的表示形式 (4)极坐标形式 A = |A|θ A=| A |(cosq + jsinq ) a=|A|cosq，b=|A|sinq A =|A| e jq ,其中 e jq =cosq +jsinq a b A a b arctan 2 2 = = + q o +j +1 A a q b (1)代数形式 A=a+jb Re[A]=a， Im[A]=b (2)指数形式 (3) 三角形式

2.复数的四则运算SDU③乘法：模相乘，辐角相加①相等T如果是其他形式表示的复数，虚部相等代数式：实部相等，应先化成极坐标式辐角相等极坐标式：模相等，④除法：模相除，辐角相减虚部②加、减：实部相加减，如果是其他形式表示的复数，相加减应先化成极坐标式部资料股设 Fi=ai+jb1,F2=|F21Z2 则F2=a2+jb2 则Fi±F2= (ai±a2)+j(bi±b2)FiF2 =|F1l|F2|Z0i+0,{Fi]Fi.请靠外如果是其他形式表示的L 0-02复数，应先化成代数式传

SDUT 内 部 资 料！ 请 勿 外 传！ F1 F2 2.复数的四则运算 ①相等： 代数式：实部相等，虚部相等 极坐标式：模相等，辐角相等 ②加、减：实部相加减，虚部 相加减 设 F1=a1+jb1 , F2=a2+jb2 则 F1±F2 = F1F2 设 F1= |F1 | ∠q1， F2= |F2 |∠q2 则 = |F1 ||F2 |∠q1+q2 ③乘法：模相乘，辐角相加 如果是其他形式表示的复数， 应先化成极坐标式 ④除法：模相除，辐角相减 如果是其他形式表示的复数， 应先化成极坐标式 (a1±a2)+j(b1±b2) 如果是其他形式表示的 复数，应先化成代数式 = ∠q1-q2 |F1 | |F2 |