《电路》课程教学资源（课后课件）有例题_第15章 -1电路方程的矩阵形式

实线连接的元素乘积减对角线法则复习1：行列式计算虚线连接的元素乘积，ala12二阶行列式：A==au1a22-al12a21a21a22a13a1a12aA三阶行列式：A=a2a222a32a3133=a11a22 a33 +a12a23 a31+a13a21 a32 -a13a22 a31 -12a23 a31-a13a21 32

a a a a A 21 22 11 12  复习1：行列式计算 二阶行列式： 实线连接的元素乘积减 虚线连接的元素乘积． 三阶行列式： 对角线法则 31 32 33 21 22 23 11 12 13 a a a a a a a a a A  =a11a22 a33 +a12a23 a31+a13a21 a32 -a13a22 a31 -a12a23 a31-a13a21 a32 a11 a12 a21 a22 a31 a32 =a11a22-a12a21

复习2：非齐次线性方程组的矩阵形式方程1:矩阵形式u,U, = Zu i, + Z12 i,[Z11 Z12 IU,]=[Z21 Z22 ] [i, U, = Z21 i, + Z22 i,Z11 Z12系数矩阵Z=Z21 Z22 -u[ii未知量矩阵[0,] [

复习2：非齐次线性方程组的矩阵形式 2 2 21 1 22 2 1 11 1 12 2 U Z I Z I U Z I Z I                 2 1 U U   未知量矩阵       2 1 I I   Z Z Z Z Z        21 22 系数矩阵 11 12       2 1 U U   Z Z Z Z       21 22 11 12       2 1 I I  矩阵形式  方程1：

方程2：U, = Z, i+Usi+Us1Ur=z,i方程变换+Us2U, =+Z, i2U, = Z, i, +Us2U,+Z, i,+Us3U, = Z, i,+Us3三11Us1U,z,矩阵形式1,U2Us2Z2+=[i.Us3]U3Z3.对角矩阵方程3：方程变换U, = Z,i +Z12 i2 +UsU, = Zu i, +Z12 i, +UsU,=Z, i, +Us2U, = Z, I, +Us2矩阵形式[Z1 Z1211[u.]Us1+[Us2iU2Z2

       3 2 1 U U U          3 2 1 Z Z Z 3 3 3 3 2 2 2 2 1 1 1 1 S S S U Z I U U Z I U U Z I U                方程变换 矩阵形式 3 3 3 3 2 2 2 2 1 1 1 1 S S S U Z I U U Z I U U Z I U                      3 2 1 I I I           S3 S2 S1 U U U    方程2：        2 1 U U         2 11 12 Z Z Z 2 2 2 2 1 11 1 12 2 1 S S U Z I U U Z I Z I U             方程变换 矩阵形式 2 2 2 2 1 11 1 12 2 1 S S U Z I U U Z I Z I U                   2 1 I I          S2 S1 U U   方程3： 对角矩阵

第15章电路方程的矩阵形式本章目录15-1割集15-2割集矩阵关联矩阵、回路矩阵、福15-3*矩阵A、之间的关系15-4回路电流方程的矩阵形式15-5结点电压方程的矩阵形式15-6割集电压方程的矩阵形式15-7*列表法

第15章 电路方程的矩阵形式 15-1 割集 15-2 关联矩阵、回路矩阵、割集矩阵 15-3* 矩阵A、Bf 、Qf 之间的关系 15-4 回路电流方程的矩阵形式 15-5 结点电压方程的矩阵形式 15-7* 列表法 15-6 割集电压方程的矩阵形式 本章目录

8重点1.割集的定义与确定；2.基本矩阵：关联矩阵、回路矩阵、割集矩阵：3.电路方程的矩阵形式①支路电路方程②回路电流(网孔电流)方程：③结点电压方程；④割集电压方程丫难点①含受控源、互感等方程矩阵形式的列写②割集电压方程。（初次接触、抽象。）5

5 ①支路电路方程； ②回路电流(网孔电流)方程； ③结点电压方程； ④割集电压方程。 难点 ①含受控源、互感等方程矩阵形式的列写； ②割集电压方程。(初次接触、抽象。) 1. 割集的定义与确定； 2. 基本矩阵：关联矩阵、回路矩阵、割集矩阵； 3. 电路方程的矩阵形式：

*引言在第三章里，我们学习了图的基本知识和电路的基本分析方法，本章是在第三章的基础上，对电路进行更深入的讨论，即应用图论的知识研究电路方程的系统列写方法及方程的矩阵形式。本章的研究目的着眼于方法的系统化，以便于利用计算机作为工具进行辅助分析。所以，学习这一章的自的是为此作理论准备的6

6 引言 在第三章里，我们学习了图的基本知识和电路 的基本分析方法，本章是在第三章的基础上， 对电路进行更深入的讨论，即应用图论的知识， 研究电路方程的系统列写方法及方程的矩阵形 式。本章的研究目的着眼于方法的系统化，以 便于利用计算机作为工具进行辅助分析。所以， 学习这一章的目的是为此作理论准备的

$15-2割集矩阵关联矩阵、回路矩阵、售研究系统化建立方程的方法，且方程用矩阵形式表示。图的矩阵表示：指用矩阵描述图的拓扑性质即KCL和KVL的矩阵形式有三种矩阵形式：哪三种?结点—支路关联矩阵回路矩阵回路一支路割集矩阵割集一支路7

7 §15-2 关联矩阵、回路矩阵、割集矩阵 研究系统化建立方程的方法，且方程用矩阵 形式表示。 图的矩阵表示：指用矩阵描述图的拓扑性质， 即KCL和KVL的矩阵形式。 有三种矩阵形式： 结点 支路 关联矩阵 回路 支路 回路矩阵 割集 支路 割集矩阵 哪三种?

1.关联矩阵A描述结点与支路的关联性质n个结点b条支路的图用nxb的矩阵A,描述：支路b结点每一行对应一个结点，nxbA=每一列对应一条支路。n(1) 元素定义支路k与结点i关联，方向背离结点；+1支路k与结点i关联，方向指向结点：aik=支路k与结点i无关背离+1,指向-1，无关0。ajk:

1. 关联矩阵A ——描述结点与支路的关联性质 每一行对应一个结点， (1) 元素定义 ajk  1 支路 k 与结点 j 关联，方向背离结点； -1 支路 k 与结点 j 关联，方向指向结点； 0 支路 k 与结点 j 无关。 Aa = nb n个结点b条支路的图用 nb 的矩阵Aa描述： 结 点 n 支路b 每一列对应一条支路。 ajk：背离1，指向-1，无关0

例：求关联矩阵A,233316isi2652A

9 例：求关联矩阵Aa i1 1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④

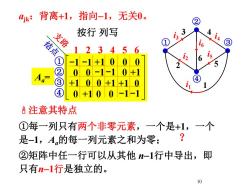
背离+1,指向-1，无关0。ajk:2按行列写33支路3结点2345isi26①??52Aa4吕注意其特点①每一列只有两个非零元素，一个是+1，一个?是-1，A,的每一列元素之和为零;②矩阵中任一行可以从其他n-1行中导出，即只有n-1行是独立的。10

10 Aa = ① ② ③ ④ 1 2 3 4 5 6 -1 -1 +1 0 0 0 0 0 -1 -1 0 +1 +1 0 0 +1 +1 0 0 +1 0 0 -1 -1 ajk：背离1，指向-1，无关0。 i1 1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④ 支 结 路 点  注意其特点 ②矩阵中任一行可以从其他 n-1行中导出，即 只有n-1行是独立的。 ？ 按行 列写 ①每一列只有两个非零元素，一个是1，一个 是-1，Aa的每一列元素之和为零；