《电路》课程教学课件（电路原理）第6章 正弦稳态电路的相量分析法（2/2）

一、单项选择题： 1.下列正弦量表达式中正确的是（) A.i=5V2sin(ot-30)A=5∠-30°A B.U=10√2sin(ot+45) C. 1=5∠-30°A D. U=10∠45Y 2.正弦电流通过电感元件时，下列关系式正确的是() A.U=L B. dt u oli C. j=-j U D.I=joLU ol 二、判断题（正确的请在圆括号内打“√”，错误的打“X” 1.电阻元件的电压有效值与电流有效值的比值是电阻R()。 2.电感元件的电压有效值与电流有效值的比值是电感L()。 3.电感元件在相位上电流超前电压90°()。 4.电容元件在相位上电流超前电压90()

1.下列正弦量表达式中正确的是（ ） A. B. C. D. 2.正弦电流通过电感元件时，下列关系式正确的是（） A. B. C. D. 二、判断题（正确的请在圆括号内打“ ” ,错误的打“ X ” 1. 电阻元件的电压有效值与电流有效值的比值是电阻R( )。 2.电感元件的电压有效值与电流有效值的比值是电感L( )。 3.电感元件在相位上电流超前电压90o ( )。 4.电容元件在相位上电流超前电压90o ( )。 √ i t A A o  = 5 2 sin( −30 ) = 5−30 10 2 sin( 45 )  U = t + I A  = 5 − 30 U V  =1045 • dt di U = L u =Li L U I j  • • = − • • I = jLU 一、单项选择题：

§6-3复阻抗和复导纳 一、复阻抗 +O 1、定义 No z29-号4w.-0-220 阻抗模|Z=U/1 阻抗角p2=Ψ4一 阻抗Z的代数形式可写为 Z=R+iX 其实部为电阻，虚部为电抗

§6-3 复阻抗和复导纳 一、复阻抗 1、定义 N0 + - • U • I def U Z I = = ( ) u i U I  −   = Z Z 阻抗模 | Z | = U / I 阻抗角 Z =u −i 阻抗 Z 的代数形式可写为 Z= R + jX 其实部为电阻，虚部为电抗

2、R、L、C对应的阻抗分别为： ZR=R Z=joL=jX 3、感抗和容抗 感抗X,=oL 反映电感对电流的阻碍作用 容抗 d 反映电容对电流的阻碍作用

2、R、L、C 对应的阻抗分别为： ZR = ZL = ZC = 3、感抗和容抗 感抗 XL =L 容抗 反映电感对电流的阻碍作用 反映电容对电流的阻碍作用 1 X C C = R jL jX = L 1 1 j C jX   C j C − = − =

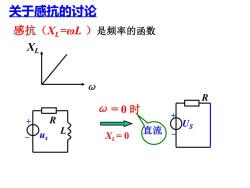
关于感抗的讨论 感抗(X,=wL)是频率的函数 XL w=0时 > U X=0 值流

感抗（XL =ωL ）是频率的函数 ω XL ω = 0 时 XL = 0 关于感抗的讨论 us + _ L R 直流 US + _ R

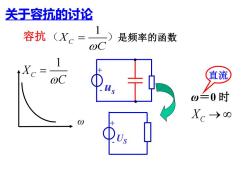
关于容抗的讨论 是频率的函数 Xc 直流 w二0时 Xc-→0

US + - ω 1 X C C = us + - 关于容抗的讨论 直流 容抗 是频率的函数 1 X C C （ = ） ω＝0 时 XC → 

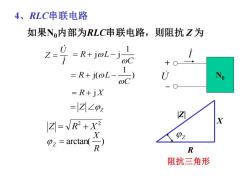
4、RLC串联电路 如果N内部为RLC串联电路，则阻抗Z为 Rjol-idc ?oy =R+j(@L- U =R+jx =|Z∠pz Z=VR2+x2 X R 阻抗三角形

4、RLC串联电路 如果N0内部为RLC串联电路，则阻抗 Z 为 U Z I = 1 R L j j C   = + − 1 R L j( ) C   = + − = + R Xj = Z Z 2 2 Z = R + X arctan( ) R X  Z = R X |Z| Z 阻抗三角形 N0 + - U I

电路的性质Z=R+j(oL- )=R+jx X pz=arctan(R） 当wL>1/wC,X>0,p>0, 电压u超前电流i,称Z呈感性； 当wL<1/wC,X<0,p<0, 电压u落后电流i,称Z呈容性； 当wL=1/wC,X=0,0=0, 电压和电流i同相，称Z呈电阻性 电路性质由什么决定？ ω一定时，电路性质由元件参数决定

当ωL > 1/ωC ，X > 0，φ>0， 电压 u 超前电流 i，称 Z 呈感性； 当ωL < 1/ωC ，X < 0，φ<0， 电压 u 落后电流 i，称 Z 呈容性； 当ωL = 1/ωC ，X = 0，φ=0， 电压 u 和电流 i 同相，称 Z 呈电阻性 电路的性质 电路性质由什么决定？ ω 一定时，电路性质由元件参数决定 1 Z R L R X j( ) j C   = + − = + arctan( ) R X  Z =

电路的性质 Z=R+oL-2)=R+jW Pz arctan( 假设R、L、C已定，电路性质能否确定？ 不能！！ 当ω不同时，可能出现： X>0,或X<0,或X=0

电路的性质 假设R、L、C已定，电路性质能否确定？ 不能！！！ 当ω不同时，可能出现： X > 0，或 X < 0 ， 或X = 0 1 Z R L R X j( ) j C   = + − = + arctan( ) R X  Z =

复阻抗与复导纳 1、复阻抗 N Z= UU/Ψ4 =zliP: I/Ψ 式中 2川=可阻抗角月，=业4 2、复导纳 Z-/Z/(cosoz+sinpz)=R+iXz X 1 -=YI Z=VR+x2 U R 二、欧姆定律的相量形式 I= U-zi i-YU U=ZI

《电路分析简明教程》 一、复阻抗与复导纳 1、复阻抗 式中) 阻抗角 2、复导纳 Z U I = U = Z I Z=|Z|(cos Z +sin Z )=R+jX 2 Z = R + X 二、欧姆定律的相量形式

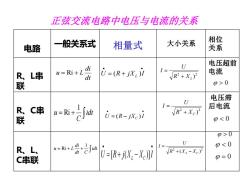
正弦交流电路中电压与电流的关系 相位 电路 一般关系式 相量式 大小关系 关系 U 电压超前 u=Ri+L U=(R+jX,)立 I= 、L串 R2+X) 电流 联 p>0 电压滞 u+之过 U R、C串 后电流 VR2+Xc) 联 U=(R-jXe)i p0 U p<0 R、L、 VR+(X:-Xc) C串联 U=[R+j(X-Xc)I p=0

正弦交流电路中电压与电流的关系 电路 一般关系式 相量式 大小关系 相位 关系 R、L串 联 电压超前 电流 R、C串 联 电压滞 后电流 R、L、 C串联 dt di u = Ri + L  = + idt C u 1 Ri • • U = R + jX I L ( ) [ ( )] U R j X X I L C • • = + − • • U = R − jX I C ( )  = + + idt dt C di u L 1 Ri   0   0 2 2 ( ) R XL X C U I + − = 2 2 ) R XL U I + = 2 2 ) R X C U I + =   0   0  = 0