《电路》课程教学课件（电路原理）含理想电压源支路、受控源的节点电压法

电路义原义理 .2含理想电压源支路、受控源的节点电压法

电 路 原 理 2.3.2 含理想电压源支路、受控源的节点电压法

含理想电压源时 电路中存在理想电压源支路时，由于该支路没有电阻，因此不能直接列 写节点电压方程，可采用下面方法进行处理。 )尽可能取电压源支路的一个极性端作为参考节点，这时该支路另一端 的节点电压成为已知量，等于该电压源电压

电路中存在理想电压源支路时，由于该支路没有电阻，因此不能直接列 写节点电压方程，可采用下面方法进行处理。 1) 尽可能取电压源支路的一个极性端作为参考节点，这时该支路另一端 的节点电压成为已知量，等于该电压源电压。 (1) 含理想电压源时

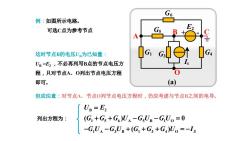
例：如图所示电路。 可选C点为参考节点 E2 C 这时节点B的电压U为已知量： UB=E2,不必再列写B点的节点电压方 程，只对节点A、O列出节点电压方程 即可。 (a) 但应注意：对节点A、节点O列节点电压方程时，仍应考虑与节点B之间的电导。 UB=E2 列出方程为： (G]+Gs+G)U-GsUg-GUo=0 -GU-G3Ug+(G]+G3+GUo=-Is

+ - G6 G5 G G4 3 G1 A B C O E2 (a) Is 例：如图所示电路。 可选C点为参考节点 但应注意：对节点A、节点O列节点电压方程时，仍应考虑与节点B之间的电导。 B 2 1 5 6 A 5 B 1 O 1 A 3 B 1 3 4 O ( ) 0 ( ) S U E G G G U G U G U G U G U G G G U I              列出方程为： 这时节点B的电压UB为已知量： UB =E2 ，不必再列写B点的节点电压方 程，只对节点A、O列出节点电压方程 即可。

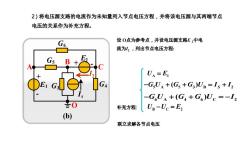
2)将电压源支路的电流作为未知量列入节点电压方程，并将该电压源与其两端节点 电压的关系作为补充方程。 设0点为参考点，并设电压源支路E,中电 流为L,列出节点电压方程： U=E -GU+(Gs+G3)UB=Is+12 -GU+(G3+Gc)Uc=-I2 补充方程： Ug-Uc=E2 (b) 联立求解各节点电压

2 ) 将电压源支路的电流作为未知量列入节点电压方程，并将该电压源与其两端节点 电压的关系作为补充方程。 + - G6 G5 G G4 3 A B C O E2 Is + - E1 (b) I2 补充方程: U U E B C 2   设 O点为参考点，并设电压源支路E 2中电 流为I2 ，列出节点电压方程: U E A 1  5 A 5 3 B 2 ( )      G U G G U I I S 6 A 4 6 C 2      G U G G U I ( ) 联立求解各节点电压

含受控源时： 对含有受控电源支路的电路，可先把受控源看作独立电源按上述方法 列方程，再将控制量用节点电压表示。 1)先把受控源当作独立电源列方程； nl gmuR2 R R R un2 RR :-is 2 2)用节点电压表示控制量。 UR2 =Unl

对含有受控电源支路的电路，可先把受控源看作独立电源按上述方法 列方程，再将控制量用节点电压表示。 1)先把受控源当作独立电源列方程； 2) 用节点电压表示控制量。 1 2 S1 1 2 1 1 1 1 ( ) n n u u i R R R    2 1 2 m 1 1 1 3 1 1 1 ( ) n n R S u u g u i R R R       u u R n 2 1  iS1 R1 R3 R2 gmuR2 + uR2 _ 2 1 (2) 含受控源时：

注意 当电路中存在电流源与电阻串联时，因为该电阻对外不起作用 故电流源支路的电阻不可列入方程中

当电路中存在电流源与电阻串联时，因为该电阻对外不起作用， 故电流源支路的电阻不可列入方程中。 注意

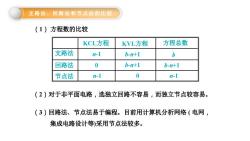
支路法、回路法和节点法的比较 (1）方程数的比较 KCL方程 KVL方程 方程总数 支路法 n-1 b-n+1 b 回路法 0 b-n+1 b-n+1 节点法 h-1 0 h-1 (2)对于非平面电路，选独立回路不容易，而独立节点较容易。 (3)回路法、节点法易于编程。目前用计算机分析网络（电网， 集成电路设计等)采用节点法较多

（2）对于非平面电路，选独立回路不容易，而独立节点较容易。 （3）回路法、节点法易于编程。目前用计算机分析网络 ( 电网， 集成电路设计等)采用节点法较多。 支路法 回路法 节点法 KCL方程 KVL方程 n-1 b-n+1 0 n-1 0 方程总数 b-n+1 n-1 b-n+1 b （1） 方程数的比较 支路法、回路法和节点法的比较

谢>谢

谢 谢