《电路》课程教学资源（课后课件）有例题_第14章 线性动态电路的复频域分析

第14章线性动态电路的复频域分析本章目录14.1拉普拉斯变换的定义14.2拉普拉斯变换的基本性质14.3拉普拉斯反变换的部分分式展开14.4运算电路14.5用拉普拉斯变换法分析线性电路14.6网络函数的定义14.7网络函数的极点和零点14.8极点、零点与冲激响应14.9极点、零点与频率响应

1 14.1 拉普拉斯变换的定义 14.2 拉普拉斯变换的基本性质 14.3 拉普拉斯反变换的部分分式展开 14.4 运算电路 14.5 用拉普拉斯变换法分析线性电路 14.6 网络函数的定义 14.7 网络函数的极点和零点 14.8 极点、零点与冲激响应 14.9 极点、零点与频率响应 本章目录 第14章 线性动态电路的复频域分析

重点①KL、元件VCR的运算形式，运算电路：②运算法的求解步骤③网络函数的定义与类型、极点与零点的概念。Y难点①正确理解和计算动态元件初始值引起的附加电源；②网络函数的零、极点与冲激响应和频率响应的关系与其它章节的联系拉氏变换：角解决电路的动态分析问题。即解决第7章的问题，称之为运算法。是后续各章的基础，是前几章基于变换思想的延续。网络函数部分以拉氏变换为基础；冲激响应参见第7章、频率响应参见第11章。2

2 ①KL、元件VCR的运算形式，运算电路； ②运算法的求解步骤； ③网络函数的定义与类型、极点与零点的概念。  难点 ①正确理解和计算动态元件初始值引起的附加电源 ； ②网络函数的零、极点与冲激响应和频率响应的关系。  与其它章节的联系 拉氏变换：解决电路的动态分析问题。即解决第 7 章的问题，称之为运算法。是后续各章的基础，是前几 章基于变换思想的延续。网络函数部分以拉氏变换为基 础；冲激响应参见第 7 章、频率响应参见第 11章

S14-1拉氏变换的定义《复变函数与积S14-2 拉氏变换的基本性质分变换》课程中学过的内容。814-3拉氏反变换的部分分式展开温故而知新长一些常用的变换①对数变换AXB= AB乘法运算变换↓↓为加法运算IgA + IgB = IgAB②相量法正弦量 i+i=i↓1l时域的正弦运算相 量+i=i变换为复数运算3

3 §14-1 拉氏变换的定义 §14-2 拉氏变换的基本性质 §14-3 拉氏反变换的部分分式展开 《复变函数与积 分变换》课程中 学过的内容。 一些常用的变换 ①对数变换 温故而知新 A × B = AB lgA 乘法运算变换 + lgB = lgAB 为加法运算 ②相 量 法 正弦量 i1 + i2 = i 时域的正弦运算 相 量 变换为复数运算 . I1 . I2 . + = I

引言长第七章研究了一阶申路和二阶电路，应用电路定律和VCR建立方程，方程为以时间为自变量的线性常微分方程，求解方程可得到时域内的解（经典法）。对具有多个动态元件的复杂电路，建立时域的高阶微分方程方程，直接求解方程工作量很大积分变换法：通过积分变换把时域函数变为频域函数，从而把时间域的高阶微分方程变换为复频域的代数方程；求出频域函数后，再做反变换，返回时域，可求得解，而不需要确定积分常数，A

4 第七章研究了一阶电路和二阶电路，应用电路定律 和VCR建立方程，方程为以时间为自变量的线性常 微分方程，求解方程可得到时域内的解（经典法）。 对具有多个动态元件的复杂电路，建立时域的高阶 微分方程方程，直接求解方程工作量很大。 积分变换法：通过积分变换把时域函数变为频域函 数，从而把时间域的高阶微分方程变换为复频域的 代数方程；求出频域函数后，再做反变换，返回时 域，可求得解，而不需要确定积分常数。 引言

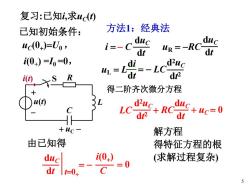
复习：已知i,求uc(t)方法1：经典法已知初始条件：ducducuc(0+)=Uo ,-RCUR =dtdti(0+) =I =0,d-ucdiuld2dtRi(t)S得二阶齐次微分方程+u(t)1duduccRC+uc= 0LC-dt?dtHH+uc-解方程由已知得得特征方程的根i(0+)(求解过程复杂)ducdtCI t=0+5

5 复习:已知i,求uC(t) 方法1：经典法 L + -u(t) i(t) C S R + uC - LC d2uC dt2 duC dt + RC + uC = 0 i = duC dt - C uR = -RC duC dt uL = L di dt = - LC d2uC dt2 得二阶齐次微分方程 uC(0+ )=U0， 已知初始条件： 由已知得 duC dt = - t=0+ C i(0+ ) = 0 i(0+ ) =I0 =0， 解方程 得特征方程的根 (求解过程复杂)

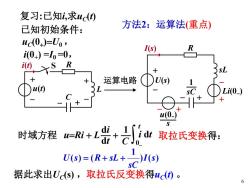
复习:已知i,求uc(t)方法2：运算法(重点)已知初始条件：uc(0+)=Uo RI(s)i(0+) =I =0,Ri(t)fSSL+十DU(s)运算电路1u(t)D Li(0.)sCC7+Hu(0.)Sdi1dt时域方程u=Ri+ L取拉氏变换得：+动U(s) =(R+ sL +I(s)Y据此求出Uc(s)，取拉氏反变换得uc(t)。6

6 时域方程 u=Ri + L di dt + 1 C ∫0- t i dt 取拉氏变换得： 运算电路 L + -u(t) i(t) C S R - + + - 方法2：运算法(重点) + sL -U(s) I(s) R - + - + Li(0- ) - + u(0-) s sC 1 ) ( ) 1 ( ) ( I s sC U s = R + sL + 据此求出UC(s) ，取拉氏反变换得uC(t) 。 uC(0+ )=U0， 已知初始条件： i(0+ ) =I0 =0， 复习:已知i,求uC(t)

1.拉氏变换定义@一个定义在[0, +] 区间的函数,f(t)，它的拉普拉斯变换式F(s)定义为：8F(s)=史 [f(t)] f(t)e-stdt0.式中s=o+jの为复数，被称为复频率F(s)称为f(t)的象函数，f(t)称为F(s)的原函数[f(t]表示取拉氏变换符号ce_-1[F(s)]表示取拉氏反变换

7 1. 拉氏变换定义 一个定义在 [0, +∞] 区间的函数 f(t)，它的拉普拉 斯变换式 F(s) 定义为： F(s)=ℒ [f(t)]= ∫ 0-∞ f(t)e -stdt 式中s=s+jw为复数，被称为复频率； F(s)称为f(t)的象函数，f(t)称为F(s)的原函数。 符号 ℒ [f(t)]表示取拉氏变换。 ℒ -1 [F(s)]表示取拉氏反变换

（应该记住）2.梳理典型函数的拉氏变换(1)单位阶跃函数 f(t) =ε(t)史 [8(t)]= (2)单位冲激函数f(t) =8(t)史 [8(t]=1(3)指数函数,f(t) = eαt (α为实数) [ea]=--aの(4)正弦函数,f(t) = sin(ot)E [sin(ot)]s2+@?S(5)余弦函数,f(t) = cos(aot)& [cos(ot)]s2+01(6)斜坡函数,f(t) = t史 []=121(7) 函数f(t) =teαte[teαt]=(s-α)S(8)函数f(t)=史 [(t) =(s+α)n+1n!常用的拉氏变换表见教材P350之表14-1。8

(s-a) 2 s-a (s+a)n+1 8 2.梳理典型函数的拉氏变换（应该记住） (1)单位阶跃函数 f(t) = e(t) ℒ [e(t)]= s 1 (2)单位冲激函数f(t) = d(t) ℒ [d(t)]=1 (3)指数函数 f(t) = e at (a为实数) ℒ [e at]= 1 (4)正弦函数 f(t) = sin(wt) (5)余弦函数 f(t) = cos(wt) ℒ [sin(wt)] = s 2+w2 w ℒ [cos(wt)] = s 2+w2 s (6)斜坡函数 f(t) = t ℒ [t]= s 2 1 常用的拉氏变换表见教材P350之表14-1。 (7) 函数 f(t) = t e at ℒ [te at]= 1 (8) 函数 n t t e n f t -a = ! 1 ( ) ℒ [f(t) ]= 1

3.本章频繁使用的拉氏变换的基本性质(1)线性性质设: [fi(t)]=Fi(s), 史 [f(t)]=F2(s)则: [Aifi(t) +A2f2(t)]= A,Fi(s) +A,F2(s)比例、叠加(2)微分性质若 [f(t)]=F(s),则 [f'(t)] =sF(s)-f(O_)推论 [f(n)(t)FsnF(s)-sn-1f(0_)-sn-2f(0_)-..--f(n-1)(0_)该性质可将f(t)的微分方程化为F(s)的代数方程(3)积分性质['f() dt=-F(s)若史[f(t)]=F(s),则e0

s 1 9 3.本章频繁使用的拉氏变换的基本性质 (1)线性性质 设：ℒ [ f1(t)]=F1(s)， 则：ℒ [A1 f1(t) +A2 f2(t)] (2)微分性质 若 ℒ [ f(t)]=F(s)， 该性质可将f (t)的微分方程化为F(s)的代数方程。 (3)积分性质 若 ℒ [ f(t)]=F(s)，则 ℒ ∫ 0- t f (t) dt = F(s) 推论 ℒ [ f (n)(t)] ℒ [ f2(t)]=F2(s) = A1F1(s) +A2F2(s) 则 ℒ [ f'(t)] = sF(s)-f(0- ) =s nF(s)-s n-1f(0- )-s n-2f'(0- )-  -f (n-1)(0- ) 比例、叠加

4.拉氏反变换c+joo方法1：利用公式F(s) est dtf(t) =2元jc-joo公式涉及到以s为变量的复变函数的积分，较复杂。工程上一般不采用这种方法。方法2：若象函数是(或稍加变换后)表14-1中所具有的形式，可直接查表得原函数A方法3：部分分式展开法：必须能运用自如！！！步骤:(1)分解为若干个简单函数之和;F(s) =Fi(s) +F2(s) + ..得原函数。(2)逐个求反变换，F(s) 反变换 f(t) =fi(t) +f2(t) + 10

10 4. 拉氏反变换 方法1：利用公式 f(t) = 2pj 1 ∫ c-j∞ c+j∞ F(s) e st dt 方法2 ：若象函数是(或稍加变换后)表14-1中所具有的 公式涉及到以 s 为变量的复变函数的积分，较复杂。 工程上一般不采用这种方法。 ∆方法3: 部分分式展开法： 形式，可直接查表得原函数。 F(s) =F1(s) +F2(s) +  f(t) =f1(t) +f2(t) +  必须能运用自如!!! 步骤:(1)分解为若干个简单函数之和; (2)逐个求反变换，得原函数。 F(s) 反变换