《电路》课程教学资源（课后课件）有例题_第9章 正弦稳态电路的分析

第9章正弦稳态电路的分析SDUT本章目录阻抗和导纳9.1电路的相量图9.2正弦稳态电路的分析9.3正弦稳态电路的功率9.4复功率9.5最大功率传输9.6外传！

SDUT 内 部 资 料！ 请 勿 外 传！ 1 第9章 正弦稳态电路的分析 本章目录 9.3 正弦稳态电路的分析 9.4 正弦稳态电路的功率 9.5 复功率 9.6 最大功率传输 9.1 阻抗和导纳 9.2 电路的相量图

重点：1.阻抗、/导纳的概念以及它们之间的等效变换2.正弦稳态电路的分析3.正弦稳态电路中功率的概念及计算包括有功功率、无功功率、视在功率、复功率、功率因数和最大功率传输Y难点应用相量图辅助分析电路的方法：复功率的概念及计算：功率因数的提高。本章与其它章节的联系请勿直流电路的分析+相量法基础1一→正弦稳态电路的分析方法，在第10～13章中都要用到。2

SDUT 内 部 资 料！ 请 勿 外 传！ 2 1. 阻抗、导纳的概念以及它们之间的等效变换 2.正弦稳态电路的分析 3.正弦稳态电路中功率的概念及计算 包括有功功率、无功功率、视在功率、复功率、功 率因数和最大功率传输  难 点 应用相量图辅助分析电路的方法； 复功率的概念及计算； 功率因数的提高。 直流电路的分析 + 相量法基础 →正弦稳态电路的分 析方法，在第10～13章中都要用到。  本章与其它章节的联系

$ 9.1SDUT阻抗和导纳阻抗Z9.1.19.1.2导纳Y部资9.1.3阻抗与导纳的相互等效请勿外传！3

SDUT 内 部 资 料！ 请 勿 外 传！ 3 §9.1 阻抗和导纳 9.1.1 阻抗 Z 9.1.2 导纳 Y 9.1.3 阻抗与导纳的相互等效

9.1.1 阻抗 ZO1.定义正弦电源激励处于稳态i+无源线性一端u口 Noi=Id;设: ü=U|Φu0lef郭UO则： Z中u-di =[Z] /Pz1资+-料！UZ2=为阻抗模;Noa具有阻碍电流的作用，单位是2。P,=du-d; 为阻抗角。请勿外之间的相位差吕阻抗两端电压与通过该阻抗电流

SDUT 内 部 资 料！ 请 勿 外 传！ 4 .I 无源线 性一端 口 N0 + - . U 设： . U = U fu . I = I fi 则：Z def . U . I = U I fu-fi = |Z| jZ |Z| = U I 为阻抗模; jz =fu-fi 为阻抗角。 具有阻碍电流的作用，单位是。 正弦电源激励 处于稳态 Z + - . U .I N0 9.1.1 阻抗 Z 1.定义  阻抗两端电压与通过该阻抗电流之间的相位差！

2.阻抗参数间的关系O+极坐标形:TZ=ZIZzUZ三角形式：: Z=z/cos@,+jlzisin0代数形式；Z=R+jX内部Z的虚部X称为电抗。Z的实部R称为电阻R =(Z/cosIZ = R2 +XX-R X=ZisinzP,= arctg(Z)X三清勿Z]、R、X构成的直角P角形称为阻抗三角形。砖！5

SDUT 内 部 资 料！ 请 勿 外 传！ 5 2.阻抗参数间的关系 5 代数形式：Z = R + j X Z的实部R称为电阻，Z的虚部X称为电抗。 R = |Z|cosjz X = |Z|sinjz jz | Z | R X |Z|、R、X构成的直角三 角形称为阻抗三角形。 极坐标形式：Z =| Z |∠jz |Z| = R2 + X2 jz = arctg R X Z + - . U .I N0 三角形式：Z =| Z |cosjz + j| Z |sinjz

阻抗表示式一SDUYIZFO+mUUZZm一1201dPz =u-Φi内部资料阻抗表示式二IZI=VR2+XR=|zicoszZ=R+jXXX=|zIsinzarctan?=7R勿外传！6

SDUT 内 部 资 料！ 请 勿 外 传！ 6 Z = R + jX R Z j Z =| | cos X Z j Z =| |sin I U Z   = 阻抗表示式二 j Z = f u -fi m m I U I U | Z |= = 2 2 | Z |= R + X R X j Z = arctan 阻抗表示式一 Z + - . U .I N0

+o3.单个元件的阻抗.SDUTUUR纯电阻=RZ=1-0+oü1必纯电感TU0U幽纯电容Z=ic+0jaciU一=jXc请勿:外传！含表明：Z可以是实数，也可以是虚数

SDUT 内 部 资 料！ 请 勿 外 传！ 7 3.单个元件的阻抗 R + - . U .I N0 L N0 + - . U .I C N0 + - . U .I  表明：Z 可以是实数，也可以是虚数。 Z = . U . I = R Z = . U . I = jwL = j XL 纯电阻 纯电感 纯电容 Z = . U . I = jwC 1 = wC 1 -j = j XC

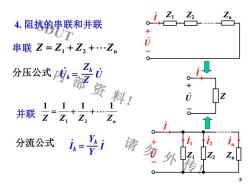
ZZ1Z24.阻抗的串联和并联JTU串联 Z = Z, + Z, +·ZOLkU分压公式式内部资料！O+UZ0并联12Z.Z.↑ti1i-yi分流公式请勿外ZK8

SDUT 内 部 资 料！ 请 勿 外 传！ 8 + - . U Z1 Z2 Zn .I Z .I - + . U Z1 Z2 Zn + - . U .I .I1 .I2 .In 分压公式 . Uk = Z Zk . U 并联 1 2 n 1 1 1 1 Z Z Z Z = + +  分流公式 .Ik = Y Yk .I 串联 Z Z1 Z2 Zn = + +  4. 阻抗的串联和并联

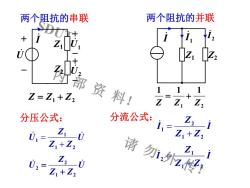
两个阻抗的并联两个阻抗的串联1+Z例部资料！1Z =Z +Z,ZZ1Z2分流公式：分压公式：Z,1Z1Z, +Z,UU, =-Z, +Z2请勿外传！Z1Z2UU,= Z,+Z

SDUT 内 部 资 料！ 请 勿 外 传！ 两个阻抗的串联 U Z Z Z U  1 2 2 2 + = 分压公式： Z = Z1 + Z2 U Z Z Z U  1 2 1 1 + = - + Z1 Z2 + - + - I  U U1 U2  Z1 Z2 I  1 I  2 I  I Z Z Z I   1 2 1 2 + = 分流公式： 1 2 1 1 1 Z Z Z = + I Z Z Z I   1 2 2 1 + = 两个阻抗的并联

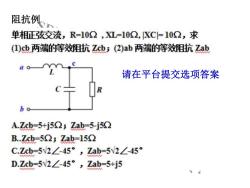
阻抗例单相正弦交流，R=102，XL-102.XC=102，求(1)cb两端的等效阻抗Zcb；（2)ab两端的等效阻抗ZabC1L请在平台提交选项答案RhA.Zcb=5+j5S2;Zab-5-j5S2B..Zcb=5S2;Zab-15S2C.Zcb-5V2-45°,Zab-5v2/-45D.Zcb-5~2/-45°，Zab=5+j5

SDUT 内 部 资 料！ 请 勿 外 传！ 阻抗例 请在平台提交选项答案