《电路》课程教学课件（电路原理）第6章 正弦稳态电路的相量分析法（总结）

一、基本概念 1、正弦量的瞬时值表达式： i=√/2sin(ωt+w:) u/2Usin(ωt+Wu) 式中包含有效值、角频率和初相位三个要素。 2、相位差 =业4：习惯上规定p≤180°。 、之间的相位关系：超前、滞后。同相、反相、正 交等。注意：任意两个同频率的正弦量都可比较其相位关 系。可借助相量图直观反映。 3、正弦量的相量：正弦量的复数表示 U=U/Ψ.1=I/4 而U卡w iti ◆严格区分电流、电压的瞬时值、最大值、有效值的 符号： i、Im、I;h、Unm、U

1、正弦量的瞬时值表达式： 式中包含有效值、角频率和初相位三个要素。 i= Isin(ωt +ψi 2 ) u= Usin(ωt +ψu 2 ) 2、相位差 j =ψu-ψi 习惯上规定|j |≤180°。 u、i之间的相位关系：超前、滞后。 同相、反相、正 交等。注意:任意两个同频率的正弦量都可比较其相位关 系。可借助相量图直观反映。 ◆严格区分电流、电压的瞬时值、最大值、有效值的 符号： i、 I m 、 I； u、 Um 、 U 而 ≠u ≠i 3、正弦量的相量:正弦量的复数表示 一、 基本概念

4.感抗X0L=2πfL为欧[姆](2)。 ◆感抗表示电感元件对正弦电流的阻碍作用。 5.容抗Xc=1/oC位为欧[姆](2)。 ◆容抗表示电容元件对正弦电流的阻 碍作用。 6.复阻抗与复导纳 U业=Z9 U Z= I/Ψ Y1 Z=Z(cosoz+sing)=R+jX ·电路的性质：Z呈感性、容性、电阻性 R

4.感抗： 单位为欧[姆]()。 ◆感抗表示电感元件对正弦电流的阻碍作用。 5.容抗： 单位为欧[姆]()。 ◆容抗表示电容元件对正弦电流的阻 碍作用。 XC =1/C 6.复阻抗与复导纳 Z=|Z|(cosj Z +sinj Z )=R+jX 电路的性质: Z 呈感性、容性、电阻性 ◆ ◆

◆复阻抗串联与分压公式 Z=Z+Z2 U=Z+Z 2 _U U,=Z+Za ◆复导纳的并联与分流公式 同理，对于个复导纳的并联电路，其等效复导纳 Yeg=Y1+Y2+.+Yn 两个复阻抗☑和☑，并联时，其等效复阻抗为 1 Z= ZZ Y+Y21+1 Z1+Z2 分流公式为 Z Z. i Zni Z i Z+Z2 1=Z*21

分流公式为 两个复阻抗Z1和Z2并联时，其等效复阻抗为 同理，对于n个复导纳的并联电路，其等效复导纳 ◆复阻抗串联与分压公式 ◆复导纳的并联与分流公式 Z=Z1+Z2 1 1 1 2 Z U U Z Z = + 2 2 1 2 Z U U Z Z = +

7.正弦稳态电路的功率 1)有功功率P=UI coso 单位：W 平均功率是网络中各电阻元件吸收的平均功率的总和 2)无功功率 O=UIsing 单位：Var 无功功率等于各储能元件无功功率的代数和。 ◆无功功率用来度量负载与电源之间能量交换的规模。 3)视在功率 S-UI 单位：VA 4)功率因数 cos o D C0S0= 5)感性负载两端并联电容器提高功率因数：P不变，Q 减小，I减小

7.正弦稳态电路的功率 1)有功功率 P =UI cosj 2)无功功率 3）视在功率 4）功率因数 S=UI Q=UIsin 平均功率是网络中各电阻元件吸收的平均功率的总和 无功功率等于各储能元件无功功率的代数和。 ◆无功功率用来度量负载与电源之间能量交换的规模。 单位：W 单位：Var 单位：VA S P cosj = 5）感性负载两端并联电容器提高功率因数：P不变，Q 减小，I减小

8.谐振（RLC串联，RL-C并联) 1)谐振的定义 含R、L、C元件的无源二端网络，则端口电压与电 流同相，二端网络呈电阻性，称电路发生了谐振。 按发生谐振的电路不同，谐振现象分为串联谐振和 并联谐振等。 2)谐振的条件 00=0= LC 3)谐振的频率 00 2元 2πVLC 4)谐振的特征 5)谐振的应用选频

8.谐振（RLC串联，RL-C并联） 1）谐振的定义 含R、L、C元件的无源二端网络，则端口电压与电 流同相，二端网络呈电阻性，称电路发生了谐振。 按发生谐振的电路不同，谐振现象分为串联谐振和 并联谐振等。 2）谐振的条件 3）谐振的频率 4）谐振的特征 5）谐振的应用：选频

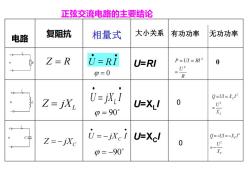
正弦交流电路的主要结论 电路 复阻抗 相量式 大小关系 有功功率 无功功率 R Z-R U=Ri U-RI P=UI=RI2 0 0=0 +0 0=I=X,2 Z=jX U=jx,I U=XI 0 0=90° +0 Z=-jXc U=-jXcI U=Xcl Q=-U1=-XI2 0 -0 p=-90°

正弦交流电路的主要结论 电路 复阻抗 相量式 大小关系 有功功率 无功功率 U=RI 0 U=XL I 0 U=XC I 0 • • U = jX I L • • U = − jX I C L Z = jX C Z = − jX Z = R R U P UI RI 2 2 = = = L L X U Q UI X I 2 2 = = = C C X U Q UI X I 2 2 = − = − = − j = 0  j = 90  j = −90

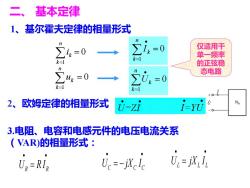
二、基本定律 1、基尔霍夫定律的相量形式 ∑4=0 仅适用干 单一频率 k= 的正弦稳 ∑4=0 态电路 k= 0&=0 k=1 2、欧姆定律的相量形式 U-zi i-ru No 3.电阻、电容和电感元件的电压电流关系 (VAR)的相量形式： UR=RIp Uc=-jXc lc U,=jX:I

1、基尔霍夫定律的相量形式 仅适用干 单一频率 的正弦稳 态电路 2、欧姆定律的相量形式 二、 基本定律 3.电阻、电容和电感元件的电压电流关系 （VAR)的相量形式： U jX I L L L • • = U jX I C C C • • = − U R I R R • • =

三、正弦稳态电路的分析方法 相量法 分析步骤是： 1、写出已知正弦电压、电流所对应的相量。 2、画出与电路的时域模型相对应的相量模型。 3、根据相量模型，利用第一章和第二章中分析 直流电阻电路的任意一种方法，列出电路复数代 数方程进行求解。最后，将求出的电压、电流相 量转换为对应的正弦量。 ◆电路的时域模型：电路元件一般以R、L、C等参数 来表征，山、是正弦时间函数。 正确作出电路的“相量模型”，是运用相量法的关键

分析步骤是： 1、写出已知正弦电压、电流所对应的相量。 2、画出与电路的时域模型相对应的相量模型。 3、根据相量模型，利用第一章和第二章中分析 直流电阻电路的任意一种方法，列出电路复数代 数方程进行求解。最后，将求出的电压、电流相 量转换为对应的正弦量。 ◆电路的时域模型：电路元件一般以R、L、C等参数 来表征，u、i是正弦时间函数。 三、正弦稳态电路的分析方法——相量法 正确作出电路的“相量模型”，是运用相量法的关键

相量图法： 利用相量图的几何关系来分析和简化计算，从而 求得所需值。它的要点是，选好一个参考相量， 通常参考相量画在水平方向。不必画出实轴和虚轴。 画成平行四边形或三角形（书中大量采用）均可 1.有一交流电压u=100sin(314t+30°)V,加在一容抗 X。=50Ω的理想电容元件两端，这时电容中的电流 i= 2.右图所示电路中ab端的等效复阻抗Zab为

相量图法： 利用相量图的几何关系来分析和简化计算，从而 求得所需值。它的要点是，选好一个参考相量， 通常参考相量画在水平方向。不必画出实轴和虚轴。 画成平行四边形或三角形（书中大量采用）均可 1.有一交流电压u=100sin(314t+30°)V， 加在一容抗 XC=50Ω的理想电容元件两端， 这时电容中的电流 i= 。 2.右图所示电路中ab端的等效复阻抗Zab为 j2 -j1

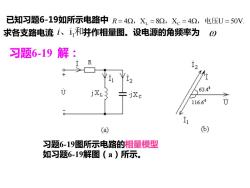
已知习题6-19如所示电路中R=42,X=82,X。=42,电压U=50V. 求各支路电流i、1和饼作相量图。设电源的角频率为0 习题6-19解： 63.q0 116.6° U (a) (b) 习题6-19图所示电路的相量模型 如习题6-19解图（a)所示

习题6-19 解： 习题6-19图所示电路的相量模型 如习题6-19解图（a）所示。 L C R =  =  =  = 4 X 8 X 4 U 50V. ， ， ，电压 1 2 i、i 和i  已知习题6-19如所示电路中 求各支路电流 并作相量图。设电源的角频率为