《电路》课程教学资源（教案讲义）第7章 一阶电路和二阶电路的时域分析

电路A教案 第七章一阶电路和二阶电路 第七章一阶电路和二阶电路 一、教学基本要求 1.掌握动态电路的特点、电路初始值的求法、零输入响应、零状态响应、全响 应、阶跃响应、冲激响应的概念和物理意义；了解二阶电路的概念及其特征方程 根的三种情况 2.会计算和分析一阶动态电路，包括三种方法： (①)全响应=零状态响应十零输入响应： (2)全响应=暂态响应十稳态响应： (3)“三要素法。 二、教学重点与难点 1.教学重点： (1)动态电路方程的建立和动态电路初始值的确定 2)一阶电路时间常数的概念： (3)一阶电路的零输入响应和零状态响应： (4)求解一阶电路的三要素方法： (⑤)自由分量和强制分量、暂态分量和稳态分量的概念。 2.教学难点： 1.应用基尔霍夫定律和电感、电容的元件特性建立动态电路方程。 2.电路初始条件的概念和确定方法。 $71动态电路的方程及其初始条件 一、动态电路 1.含有动态元件电容和电感的电路称动态电路。 2.因此动态电路的特点是：当电路状态发生改变时（换路）需要经历一个变化 过程才能达到新的稳定状态。这个变化过程称为电路的过渡过程。 3.电阻电路、电容电路和电感电路在换路时的表现。 纯电阻电路在换路时没有过渡期。 含电容和电感的电路在换路时需要一个过渡期。 二、动态电路的方程 第1页共19页

电路 A 教案 第七章 一阶电路和二阶电路 第 1 页 共 19 页 一、教学基本要求 1. 掌握动态电路的特点、电路初始值的求法、零输入响应、零状态响应、全响 应、阶跃响应、冲激响应的概念和物理意义 ；了解二阶电路的概念及其特征方程 根的三种情况。 2. 会计算和分析一阶动态电路，包括三种方法： ⑴全响应＝零状态响应＋零输入响应； ⑵全响应＝暂态响应＋稳态响应； ⑶“三要素”法。 二、教学重点与难点 1. 教学重点： (1)动态电路方程的建立和动态电路初始值的确定； (2)一阶电路时间常数的概念； (3)一阶电路的零输入响应和零状态响应； (4)求解一阶电路的三要素方法； (5)自由分量和强制分量、暂态分量和稳态分量的概念。 2．教学难点： 1. 应用基尔霍夫定律和电感、电容的元件特性建立动态电路方程。 2. 电路初始条件的概念和确定方法。 §7.1 动态电路的方程及其初始条件 一、动态电路 1．含有动态元件电容和电感的电路称动态电路。 2. 因此动态电路的特点是：当电路状态发生改变时（换路）需要经历一个变化 过程才能达到新的稳定状态。这个变化过程称为电路的过渡过程。 3. 电阻电路、电容电路和电感电路在换路时的表现。 纯电阻电路在换路时没有过渡期。 含电容和电感的电路在换路时需要一个过渡期。 二、动态电路的方程

电路A教案 射七章一阶电路和二阶电路 分析动态电路，首先要建立描述电路的方程。动态电路方程的建立包括两部分内 容：一是应用基尔霍夫定律，二是应用电感和电容的微分或积分的基本特性关系式。 综合得以下结论： (1)描述动态电路的电路方程为微分方程： (2)动态电路方程的阶数等于电路中动态元件的个数，一般而言，若电路中含 有n个独立的动态元件，那么描述该电路的微分方程是n阶的，称为n阶电路： (3)描述动态电路的微分方程的一般形式为 a密+a=020 描述一阶电路的方程是一阶线性微分方程，描述二阶电路的方程是二阶线性微分 方程 a密+4020 高阶电路的方程是高阶微分方程： d*4x 方程中的系数与动态电路的结构和元件参数有关。 三.换路定则 1,换路的概念：电路的结构和参数变化引起的电路的变化统称为换路。 若把电路发生换路的时刻记为0时刻，换路前一瞬间记为0-，换路后一瞬间记 为0+，则初始条件为0+时山，i及其各阶导数的值 2.换路定律：(0)=(0)，0)=i(0)。 四、电略初始条件的确定 根据换路定律可以由电路的(0-)和立(0-)确定c(0+)和(0+)时刻的 值，电路中其他电流和电压在0+时刻的值可以通过0+等效电路求得。求初始值的具 体步骤是： 1.由换路前=0-时刻的电路（一般为稳定状态）求c(0-)或L(0-); 2.由换路定律得c(0+)和n.(0+): 3.画0+时刻的等效电路：电容用电压源替代，电感用电流源替代（取0+时刻 值，方向与原假定的电容电压、电感电流方向相同)： 第2页共19页

电路 A 教案 第七章 一阶电路和二阶电路 第 2 页 共 19 页 分析动态电路，首先要建立描述电路的方程。动态电路方程的建立包括两部分内 容：一是应用基尔霍夫定律，二是应用电感和电容的微分或积分的基本特性关系式。 综合得以下结论： （1）描述动态电路的电路方程为微分方程； （2）动态电路方程的阶数等于电路中动态元件的个数，一般而言，若电路中含 有 n 个独立的动态元件，那么描述该电路的微分方程是 n 阶的，称为 n 阶电路； （3）描述动态电路的微分方程的一般形式为 描述一阶电路的方程是一阶线性微分方程，描述二阶电路的方程是二阶线性微分 方程 高阶电路的方程是高阶微分方程： 方程中的系数与动态电路的结构和元件参数有关。 三. 换路定则 1．换路的概念：电路的结构和参数变化引起的电路的变化统称为换路。 若把电路发生换路的时刻记为 t=0 时刻，换路前一瞬间记为 0－，换路后一瞬间记 为 0＋，则初始条件为 t=0＋时 u，i 及其各阶导数的值。 2. 换路定律: (0 ) (0 ) C C u u + − = ， (0 ) (0 ) L L i i + − = 。 四、电路初始条件的确定 根据换路定律可以由电路的 uC（0－）和 iL（0－）确定 uC（0+）和 iL（0+）时刻的 值,电路中其他电流和电压在 t=0+时刻的值可以通过 0+ 等效电路求得。求初始值的具 体步骤是： 1. 由换路前 t=0－时刻的电路（一般为稳定状态）求 uC （0－） 或 iL （0－）； 2. 由换路定律得 uC （0+） 和 iL （0+） ； 3. 画 t=0+时刻的等效电路：电容用电压源替代，电感用电流源替代（取 0+时刻 值，方向与原假定的电容电压、电感电流方向相同）；

电路A教案 第七章一阶电路和二阶电路 4.由04电路求所需各变量的0+值。 注意：直流稳态时电感相当于短路，电容相当于断路。 S72一阶电路的零输入响应 动态电路的零输入响应是指换路后外加激励为零，仅由动态元件初始储能所产生 的电压和电流。 一、RC电路的零输入响应 K(t=0) 图示RC电路在开关闭合前己充电，电容电压 (0)=U。,开关闭合后，根据KVL可得 +。=0,由于-c验 代入上式得微分方程： RC血+=0,4,0，)=(0)=U 1 特征方程为RCp+=0,特征根为： p=-RC 则方程的通解为：。=4e”=A完，代入初始值得：4：40)= u,=4,0+e面=U,e密t≥0 或根据电容的VCR计算： 。品 i-c4-cvo) 从以上各式可以得出 1)电压、电流是随时间按同一指数规律衰减的函数，如下图所示 %% 连续函 T小 2)响应与初始状态成线性关系，其衰减快慢与RC有关。令=RC,的量 纲为： 第3页共19页

电路 A 教案 第七章 一阶电路和二阶电路 第 3 页 共 19 页 4 .由 0+电路求所需各变量的 0+值。 注意：直流稳态时电感相当于短路，电容相当于断路。 §7.2 一阶电路的零输入响应 动态电路的零输入响应是指换路后外加激励为零，仅由动态元件初始储能所产生 的电压和电流。 一、RC 电路的零输入响应 图示 RC 电路在开关闭合前已充电，电容电压 0 (0 ) C u U − = ，开关闭合后，根据 KVL 可得： ，由于 ， 代入上式得微分方程： 0 C C du RC u dt + = ， 0 (0 ) (0 ) C C u u U + − = = 特征方程为 RCp+ 1=0 ，特征根为： 则方程的通解为： ，代入初始值得： 0 (0 ) A u U = = C + ， 放电电流为： 或根据电容的 VCR 计算： 从以上各式可以得出 1）电压、电流是随时间按同一指数规律衰减的函数，如下图所示； 2）响应与初始状态成线性关系，其衰减快慢与 RC 有关。令 τ= RC ，τ 的量 纲为：

电路A教案 第七章一阶电路和二阶电路 -]-要]倒 τ为一阶电路的时间常数。τ的大小反映了电路过渡过程时间的长短，即： τ大一过渡过程时间长，t小→过渡过程时间短，如图所示。表中的数据表 明经过一个时间常数，电容电压衰减到原来电压的36.8%，因此，工程上认为，经 过3r一5红，过渡过程结束。 3)在放电过程中，电容释放的能量全部被电阻所消耗，即： 二、RL电略的零输入响应 图示L电路，在开关动作前电压和电流己恒定不变，因此电感电流的初值为： 0)=0)=4R 开关闭合后电路： 根据KCVL可得：g+z=0 K作0)L4 Ug=Ri 代入上式得微分方程 +=0t≥0 特征方程为：LP+R=0,特征根 则方程的通解为：i)=Ae” 代入初始值得：A=,0)=1。 10=e”.et20 R+R =-RIoe TrR 电感电压为： t 从以上各式可以得出： (1)电压、电流是随时间按同一指数规律衰减的函数。 第4页共19页

电路 A 教案 第七章 一阶电路和二阶电路 第 4 页 共 19 页 τ 为一阶电路的时间常数。τ 的大小反映了电路过渡过程时间的长短，即： τ 大 → 过渡过程时间长，τ 小 → 过渡过程时间短，如图所示。表中的数据表 明经过一个时间常数 τ，电容电压衰减到原来电压的 36.8%，因此，工程上认为，经 过 3τ－5τ,过渡过程结束。 3）在放电过程中，电容释放的能量全部被电阻所消耗，即： 二、RL 电路的零输入响应 图示 RL 电路，在开关动作前电压和电流已恒定不变，因此电感电流的初值为： 开关闭合后电路： 根据 KCVL 可得： 把 代入上式得微分方程： 特征方程为： Lp+R= 0 ， 特征根 则方程的通解为： ，代入初始值得： 0 (0 ) A i I = = L + 电感电压为： 从以上各式可以得出： （1） 电压、电流是随时间按同一指数规律衰减的函数

电路A教案 第七章一阶电路和二阶电路 U 跃变 0 -RIY (2)响应与初始状态成线性关系，其衰减快慢与山R有关。令仁L/R,称为 一阶L电路时间常数，满足： -白豪被刷 (3)在过渡过程中，电感释放的能量被电阻全部消耗，即： m-R=aep脉=a-e0r-团 2 三、小结 1.一阶电路的零输入响应是由储能元件的初值引起的响应，都是由初始值衰减 为零的指数衰减函数，其一般表达式可以写为 0=y0*e 2.零输入响应的衰减快慢取决于时间常数，其中RC电路RC,RL电路=LR。 R为与动态元件相连的一端口电路的等效电阻。 3.同一电路中所有响应具有相同的时间常数。 4.一阶电路的零输入响应和初始值成正比，称为零输入线性。 四、用经典法求解一阶电路零输入响应的步骤： 1.根据基尔霍夫定律和元件特性列出换路后的电路微分方程，该方程为一阶线 性齐次常微分方程： 2.由特征方程求出特征根： 3.根据初始值确定积分常数从而得方程的解。 73一阶电略的零状态响应 一阶电路的零状态响应是指动态元件初始能量为零，1>0后由电路中外加输入激 励作用所产生的响应。 一、RC电路的零状态响应 开关闭合后，根据KVL可得： 第5页 共19页

电路 A 教案 第七章 一阶电路和二阶电路 第 5 页 共 19 页 （2）响应与初始状态成线性关系，其衰减快慢与 L/ R 有关。令 τ= L / R，称为 一阶 RL 电路时间常数， 满足： （3）在过渡过程中，电感释放的能量被电阻全部消耗，即： 三、小结 1. 一阶电路的零输入响应是由储能元件的初值引起的响应，都是由初始值衰减 为零的指数衰减函数，其一般表达式可以写为 2. 零输入响应的衰减快慢取决于时间常数 τ，其中 RC 电路 τ=RC ，RL 电路 τ=L/R。 R 为与动态元件相连的一端口电路的等效电阻。 3. 同一电路中所有响应具有相同的时间常数。 4. 一阶电路的零输入响应和初始值成正比，称为零输入线性。 四、用经典法求解一阶电路零输入响应的步骤： 1. 根据基尔霍夫定律和元件特性列出换路后的电路微分方程，该方程为一阶线 性齐次常微分方程； 2. 由特征方程求出特征根； 3. 根据初始值确定积分常数从而得方程的解。 §7.3 一阶电路的零状态响应 一阶电路的零状态响应是指动态元件初始能量为零，t＞0 后由电路中外加输入激 励作用所产生的响应。 一、RC 电路的零状态响应 开关闭合后，根据 KVL 可得：

电路A教案 菲七章一阶电路和二阶电路 ug +uc=Us 方程c告+= K(0) 由初始条件4(0，)=0，得方程解： Us g 4,=U。-Ue嘉-U,1-e)(t≥0) 14c0门)=0 从上式可以得出电流： dt 从以上各式可以得出 (1)电压、电流是随时间按同一指数规律变化的函数，电容电压由两部分构成： 稳态分量（强制分量）+暂态分量（自由分量） (2)响应变化的快慢，由时间常数=RC决定：τ大，充电慢，T小充电就快。 (3)响应与外加激励成线性关系： (4)充电过程的能量关系为： 电容最终储存能量： 电源提供的能量为 W=J6tU,idt=U,9=CU月 电阻消耗的能量为： Wa=j6Rt=e子Rt 二、RL电路的零状态响应 用类似方法分析图所示的RL电路。电路在开关闭合前处于零初始状态，即电感 电流L(0)=0,开关闭合后，根据KCL、KVVL可得：：+，=Ug K(F) 把 = L+Ri:=Us 代入上式得微分方程： dt 第6页共19页

电路 A 教案 第七章 一阶电路和二阶电路 第 6 页 共 19 页 方程 C C S du RC u U dt + = ， 由初始条件 (0 ) 0 C u + = ，得方程解: 从上式可以得出电流： 从以上各式可以得出 （1）电压、电流是随时间按同一指数规律变化的函数，电容电压由两部分构成： 稳态分量（强制分量）+暂态分量（自由分量） （2）响应变化的快慢，由时间常数 τ＝ RC 决定；τ 大，充电慢，τ 小充电就快。 （3）响应与外加激励成线性关系； （4）充电过程的能量关系为： 电容最终储存能量： 电源提供的能量为： 电阻消耗的能量为： 二、RL 电路的零状态响应 用类似方法分析图所示的 RL 电路。电路在开关闭合前处于零初始状态，即电感 电流 iL（0－）=0 ，开关闭合后，根据 KCL、KVVL 可得： 把 代入上式得微分方程：

电路A教案 第七章一阶电路和二阶电路 由初始条件，0+)=0，得积分常数 A=_U R 用4-警0 4,=L=Ue子 4ze)=10×Rne-10e=2000e10e7 §7.4一阶电略的全响应 一阶电路的全响应是指换路后电路的初始状态不为零，同时又有外加激励源作用 时电路中产生的响应。 一、全响应 RC串联电路为例： 稳态解 暂态解 电路微分方程为： RC密+。=巧 所以电路的全响应为：4。=Ug+4e2=U,+心。-0，)e÷t≥0 二、全响应的两种分解方式 1.上式的第一项是电路的稳态解，第二项是电路的暂态解，因此一阶电路的全 响应可以看成是稳态解加暂态解，即 全响应=强制分量（稳态解）+自由分量（暂态解） 2.把上式改写成 uc=U:(-ei)+Ue t20) 显然第一项是电路的零状态解，第二项是电路的零输入解，因此一阶电路的全响 应也可以看成是零状态解加零输入解，即 全响应=零状态响应+零输入响应 第7页共19页

电路 A 教案 第七章 一阶电路和二阶电路 第 7 页 共 19 页 由初始条件 ， 得积分常数 则 §7.4 一阶电路的全响应 一阶电路的全响应是指换路后电路的初始状态不为零，同时又有外加激励源作用 时电路中产生的响应。 一、全响应 RC 串联电路为例： 电路微分方程为： 所以电路的全响应为： 二、全响应的两种分解方式 1. 上式的第一项是电路的稳态解，第二项是电路的暂态解，因此一阶电路的全 响应可以看成是稳态解加暂态解，即 全响应 = 强制分量 （ 稳态解 ）+ 自由分量 （ 暂态解 ） 2. 把上式改写成 显然第一项是电路的零状态解，第二项是电路的零输入解，因此一阶电路的全响 应也可以看成是零状态解加零输入解，即 全响应=零状态响应+零输入响应

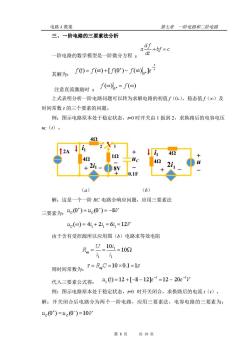
电路A教案 第七章一阶电路和二阶电路 三、一阶电略的三要素法分析 adf+时=c 阶电路的数学模型是一阶微分方程： dt 其解为：f0=fo）+[/0')-了o列k 注意直流激励时： f(o+=f(∞) 上式表明分析一阶电路问题可以转为求解电路的初值∫(0+)，稳态值∫（∞）及 时间常数π的三个要素的问题。 例：图示电路原本处于稳定状态，0时开关由1扳到2，求换路后的电容电压 c(t)。 2 2A 4 12 2i- 42 8V 2 十 0.1F (a) (b) 解：这是一个一阶RC电路全响应问题，应用三要素法 三要素为：40*)=40)=-8 c(o)=4+24=61=127 由于含有受控源所以应用图(b)电路求等效电阻 R,-9-104-100 则时间常数为：T=R,C=10×0.1=15 代入三要素公式得：，0=12+[-8-12业=12-20e*y 例：图示电路原本处于稳定状态，0时开关闭合，求换路后的电流1()。 解：开关闭合后电路分为两个一阶电路，应用三要素法，电容电路的三要素为： u0)=uc(0)=10V 第8项共19项

电路 A 教案 第七章 一阶电路和二阶电路 第 8 页 共 19 页 三、一阶电路的三要素法分析 一阶电路的数学模型是一阶微分方程 ： 其解为： 注意直流激励时 ： 上式表明分析一阶电路问题可以转为求解电路的初值 f（0+），稳态值 f（∞）及 时间常数 τ 的三个要素的问题。 例：图示电路原本处于稳定状态，t=0 时开关由 1 扳到 2，求换路后的电容电压 uC（t）。 （a） （b） 解：这是一个一阶 RC 电路全响应问题，应用三要素法 三要素为： 由于含有受控源所以应用图（b）电路求等效电阻 则时间常数为： 代入三要素公式得： 例：图示电路原本处于稳定状态，t=0 时开关闭合，求换路后的电流 i（t）。 解：开关闭合后电路分为两个一阶电路，应用三要素法，电容电路的三要素为：

电路A教案 个路和二阶市 ue(∞)=0.71=RwC=2×0.25=0.5s 电感电路的三要素为： iz(0)=i,(0)=0.,(∞)=10/5=2A t2=L/Rm=1/5=0.2s 代入三要素公式得：4)=6，(o)+[4,(0)-4,(o小e=10e7 ize)=iz(o)+[,(0*)-i,(∞小eF=21-e)A 因出.0-0+49-20-e+5e4 2 例：已知：电感无初始储能，0时闭合开关1,0.2s 时闭合开关2，求两次换路后的电感电流1(1)。 解：分两个阶段求解，当002s时，根据：0.2)=2-2e02=1.26,有 i(0.2*)=1.26A 因为：名3=L/R=1/2=0.5()=10/2=5A 所以：i0=5-3.74e2021A S7.7一阶电路的阶跃响应 一、单位阶跃函数 1.单位阶跃函数的定义 )= 0e0) ,L0 第9页 共19页

电路 A 教案 第七章 一阶电路和二阶电路 第 9 页 共 19 页 ， 电感电路的三要素为： ， ， 代入三要素公式得： 因此： 例：已知：电感无初始储能，t=0 时闭合开关 k1, t=0.2s 时闭合开关 k2，求两次换路后的电感电流 i（t）。 解：分两个阶段求解，当 0＜t＜0.2s 时有： 所以： 当 t＞0.2s 时，根据： ，有 因为： 所以： §7.7 一阶电路的阶跃响应 一、单位阶跃函数 1. 单位阶跃函数的定义 单位阶跃函数。可定义为：

电路A教案 射七章一阶电路和二阶电路 任一时刻to起始的阶跃函数，也称为延迟的单位阶跃函数，可定义为： e-w-888 E(t-to) 2.单位阶跃函数的作用 (1)可以用来描述开关动作。 ol to (2)可以用来起始一个任意函数，即： f0t-0jee2) 0(t≤t。) (3)可以用来延迟一个函数。 (4)可以用来表示复杂的信号，如图所示函数可 以写为： f0=s0-t-6) 二、一阶电路的阶跃响应 阶跃响应是指激励为单位阶跃函数时，电路中产生的零状态响应。以C电路 受直流阶跃激励为例加以说明。 根据阶跃函数的性质得：4e(0.)=0,4e(o)=1。 所以阶跃响应为：“心=1-g忘后00=子。扇6的 c0= 注意：1=e产0（初值为零）和1=e京，1≥0（初值可以不为零）的区别。 若上述激励在1=0时加入，则响应从1=0开始。即： 40=0-e宽)at-t)）。-e资e-t) 注意：上式为延迟的阶跃响应，不要写为 第10页共19页

电路 A 教案 第七章 一阶电路和二阶电路 第 10 页 共 19 页 任一时刻 t0 起始的阶跃函数，也称为延迟的单位阶跃函数，可定义为： 2. 单位阶跃函数的作用 （1）可以用来描述开关动作。 （2）可以用来起始一个任意函数，即： （3）可以用来延迟一个函数。 （4）可以用来表示复杂的信号，如图 所示函数可 以写为： 二、一阶电路的阶跃响应 阶跃响应是指激励为单位阶跃函数时，电路中产生的零状态响应。以 RC 电路 受直流阶跃激励为例加以说明。 根据阶跃函数的性质得： (0 ) 0 C u − = ， ( ) 1 C u  = 。 所以阶跃响应为： 注意： ( ) t RC i e t  − = （初值为零） 和 , 0 t RC i e t − =  （初值可以不为零）的区别。 若上述激励在 t = t0 时加入，则响应从 t = t0 开始。即： 注意：上式为延迟的阶跃响应，不要写为