《电路》课程教学资源（PPT课件讲稿）第9章 正弦稳态电路分析

第九章正弦稳态电路的分析 学习要点 1. 阻抗和导纳的定义及含义： 2.电路的相量图； 3.一般正弦稳态电路的分析方法一电阻电路 分析方法的推广； 4.瞬时功率、有功功率、无功功率、视在功 率、功率因数、复功率的概念与计算； 5.有功功率、无功功率的测量； 6.最大功率传输条件及其计算； 1

1 第九章 正弦稳态电路的分析 1. 阻抗和导纳的定义及含义； 2. 电路的相量图； 3. 一般正弦稳态电路的分析方法—电阻电路 分析方法的推广； 4. 瞬时功率、有功功率、无功功率、视在功 率、功率因数、复功率的概念与计算； 5. 有功功率、无功功率的测量； 6. 最大功率传输条件及其计算； 学习要点

重点 ©复阻抗、复导纳的概念以及它们之 间的等效变换； ©正弦稳态电路的分析； ©正弦稳态电路中的平均功率、无功 功率、视在功率、复功率、功率因 数的概念及计算； ©最大功率传输。 2

2 重点 ·复阻抗、复导纳的概念以及它们之 间的等效变换； ¸正弦稳态电路的分析； ¹正弦稳态电路中的平均功率、无功 功率、视在功率、复功率、功率因 数的概念及计算； º最大功率传输

难点 Y复阻抗和复导纳的概念； Y直流电路的分析方法及定理在正弦稳态电 路分析中的应用； Y正弦稳态电路中的功率与能量关系，如平 均功率、无功功率、视在功率、复功率、 功率因数的概念及计算； Y应用相量图分析电路的方法。 本章与其它章节的联系 直流电路的分析+相量法基础→正弦稳态电路 的分析方法，在第10、11、12章节中都要用到。 3

3 难点 复阻抗和复导纳的概念； 直流电路的分析方法及定理在正弦稳态电 路分析中的应用； 正弦稳态电路中的功率与能量关系，如平 均功率、无功功率、视在功率、复功率、 功率因数的概念及计算； 应用相量图分析电路的方法。 直流电路的分析 + 相量法基础 → 正弦稳态电路 的分析方法，在第10、11、12章节中都要用到。 本章与其它章节的联系

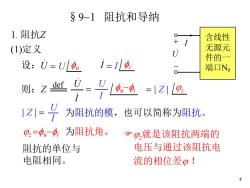
§9-1阻抗和导纳 1.阻抗☑ + 含线性 (1)定义 无源元 件的一 设：U=Up 4i-1l4 端口No 1z1=9 为阻抗的模，也可以简称为阻抗。 0=中一功，为阻抗角。 gp,就是该阻抗两端的 阻抗的单位与 电压与通过该阻抗电 电阻相同。 流的相位差0！ 4

4 §9-1 阻抗和导纳 1. 阻抗Z (1)定义 Fjz就是该阻抗两端的 电压与通过该阻抗电 流的相位差j ！ .I 含线性 无源元 件的一 端口N0 + - . U 设： .U = U fu .I = I fi 则：Z def .U .I = U I fu-fi = | Z | jz | Z | = U I 为阻抗的模，也可以简称为阻抗。 jz =fu-fi 为阻抗角。 阻抗的单位与 电阻相同

(2)阻抗参数间的关系 指数式：Z=|Zejo: 极坐标式：Z=|Z 代数式：Z=Z]coso.+jZ sing No Z=R+jx Z的实部R称为电阻，Z的虚部X称为电抗。 (R=l☑cosp ∫☑=VR2+2 X=l☑sinp. a=ang言 Z\ X ☑、R、X构成的直角三 p 角形称为阻抗三角形。 R 5

5 (2)阻抗参数间的关系 指数式：Z=| Z | e jj z 代数式：Z =| Z |cosjz + j| Z |sinjz Z = | Z | jz Z = R + j X Z的实部R称为电阻，Z的虚部X称为电抗。 Z + - . U .I N0 R = |Z|cosjz X = |Z|sinjz jz | Z | R X |Z|、R、X构成的直角三 角形称为阻抗三角形。 极坐标式： |Z| = R2 + X2 jz = arctg R X

(3)单个元件的阻抗 纯电阻乙= U=R 纯电感 Z= U-joL.=jXi X=oL称感性电抗，X,∝f! 纯电容7号d=成jX 称容性电抗，Xc∝(1f):U 说明Z可以是纯实数， 也可以是纯虚数

6 (3)单个元件的阻抗 R + - . U .I N0 L N0 + - . U .I C N0 + - . U .I 说明 Z 可以是纯实数， 也可以是纯虚数。 Z = .U .I = R Z = .U .I = jwL = j XL 纯电阻 纯电感 XL=wL 称感性电抗，XL∝f ！ 纯电容 Z = .U .I = jwC 1 = wC 1 -j = j XC XC = - wC 1 称容性电抗，XC∝(1/f ) ！

(4)RLC串联电路 根据KVL和VCR的 +UR 相量形式可得： U-RI+joLi-joCi -(R+jol-jnC]i=[R+j(Xi+Xc)li =(R+jx)I=ZI U=R+jX=1Z110 X=Xi+Xc=oL-oc X p=arctg R

7 (4)RLC串联电路 根据KVL和VCR的 相量形式可得： .U = wL- wC 1 + - + - R jwL + - . UR . UL . UC jwC 1 + - . U .I = R N0 .I + jwL .I - jwC 1 .I = R + jwL- wC 1 . j I = [R + j(XL+XC)] .I . = (R + jX)I = Z .I Z = .I .U = R + j X = | Z | jz X = XL + XC jz = arctg R X

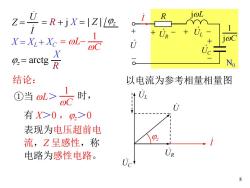
Z=立=R+jX=|ZIg X=XL+Xc=0L-1 UR U元 C .=arctgR 结论： 以电流为参考相量相量图 ①当oL> @C 时， 有X>0,0>0 表现为电压超前电 流，Z呈感性，称 电路为感性电路。 UR

8 + - + - R jwL + - . UR . UL . UC jwC 1 + - . U .I N0 Z = .I .U = R + j X = | Z | jz = wL- wC 1 X = XL + XC jz = arctg R X ①当 wL＞ 结论： 表现为电压超前电 流，Z 呈感性，称 电路为感性电路。 wC 1 时， 有 X＞0 ，jz＞0 以电流为参考相量相量图 .I . . UR UC . UL .U jz

=R+i=11@ 1= 10 X=XL+Xc =0L-I +UR C X p-=arctg R 以电流为参考相量相量图 ②当 时， U Ur 有X<0,p<0。 表现为电压滞后电 流，Z呈容性，称 电路为容性电路。 9

9 ②当 wL＜ 表现为电压滞后电 流，Z 呈容性，称 电路为容性电路。 wC 1 时， 有 X＜0 ，jz＜0。 .I . UR . UC . UL jz 以电流为参考相量相量图 + - + - R jwL + - . UR . UL . UC jwC 1 + - . U .I N0 Z = .I .U = R + j X = | Z | jz = wL- wC 1 X = XL + XC jz = arctg R X

Z=立=R+jX=|ZIg X=XL+Xc=0L-I UR C X .=arctg 以电流为参考相量相量图： t Ul 8从相量图可以 有X=0,p=0。 看出，正弦交 表现为电压与电流 U=UR 流RLC串联电 同相位，电路发生 路中，会出现 了串联谐振，Z呈 分电压大于总 纯电阻性。 电压的现象。 Uc 10

10 ③当 wL = 表现为电压与电流 同相位，电路发生 了串联谐振，Z 呈 纯电阻性。 wC 1 时， 有 X = 0 ，jz = 0。 .I . UR . UC . UL .U 以电流为参考相量相量图： = 从相量图可以 看出，正弦交 流RLC串联电 路中，会出现 分电压大于总 电压的现象。  + - + - R jwL + - . UR . UL . UC jwC 1 + - . U .I N0 Z = .I .U = R + j X = | Z | jz = wL- wC 1 X = XL + XC jz = arctg R X