《电路》课程教学资源(PPT课件讲稿)第8章 相量法

第八章相量法 内容提要 1.正弦量及其三要素、相位差的概念; 2.相量法的概念及其性质; 3.电路定律和元件VCR的相量形式。 4Im=5∠45oA Um 450 Z= =20∠-4502 Um=100∠0oV
1 第八章 相量法 内容提要 1.正弦量及其三要素、相位差的概念; 2.相量法的概念及其性质; 3.电路定律和元件VCR的相量形式。 .Im = 5∠45 o A .Um = 100∠0 o V 45 o Z = .Um .Im =20∠-45 o W

重点 1.正弦量和相量之间的关系: 2.正弦量的相量差和有效值的概念; 3.R、L、C各元件的电压、电流关系的相量形式; 4.电路定律的相量形式及元件的电压电流关系的 相量形式。 难点 1.正弦量与相量之间的联系和区别; 2.元件电压相量和电流相量的关系。 主要是相位关系,是学习第9~12章的基础, 必须熟练掌握相量法的解析运算。 2
2 重点 难点 1. 正弦量与相量之间的联系和区别; 2. 元件电压相量和电流相量的关系。 1.正弦量和相量之间的关系; 2.正弦量的相量差和有效值的概念; 3. R、L、C各元件的电压、电流关系的相量形式; 4.电路定律的相量形式及元件的电压电流关系的 相量形式。 主要是相位关系,是学习第 9~12 章的基础, 必须熟练掌握相量法的解析运算

§8-1复数 1.复数的表示形式 (3)指数和极坐标形式 (1)代数形式F=a+jb 根据欧拉公式 Re[F]=a,Im[F]=b ejo=cos0+isin0 (2)三角形式 得指数形式: F=lF(cosθ+jsinθ) F=F eio a=Flcose,b=Flsine 或写成极坐标形式: 1F|=a2+b2 F=|F10 b 0=arctg a 3
3 §8-1 复数 1. 复数的表示形式 (1)代数形式 F=a+jb Re[F]=a, Im[F]=b (2) 三角形式 F=| F |(cosq + jsinq ) a=| F |cosq,b=| F |sinq (3)指数和极坐标形式 根据欧拉公式 e jq =cosq +jsinq 得指数形式: F = | F | e jq 或写成极坐标形式: | F | = a 2 + b 2 F = | F | q q = arctg b a
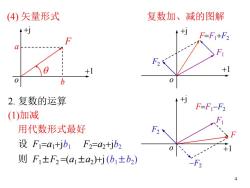
(4)矢量形式 复数加、减的图解 +] F=F+F2 +1 +1 b 2.复数的运算 F=F-F2 (1)加减 用代数形式最好 设F1=a1+jb1F2=a2+jb2 则F1±F2=(a1±2)+j(b1±b2) 4
4 (4) 矢量形式 2. 复数的运算 (1)加减 用代数形式最好 设 F1=a1+jb1 F2=a2+jb2 则 F1±F2 =(a1±a2)+j(b1±b2) 复数加、减的图解 o +j +1 F a b q +j o +1 F1 F2 F=F1+F2 F=F1-F2 -F2 +j o +1 F1 F2 F

(2)乘除 用指数或极坐标形式最好 F=Feio,F2=F2 ej2 则F=F1F2=|F1l川F2lej6+o) 或F=IFIF2l/0+A F= F3-F2 /0-6 乘(除)法运算满足模相乘(除),辐角相加(减)。 8若两个复数相等F1=F2 则必须是Fl=F2引,0=0 或是a1=a2,jb=jb2
5 (2) 乘除 用指数或极坐标形式最好 设 F1= | F1 | e jq 1, F2 = | F2 | e jq 2 则 F=F1 F2 = | F1 | | F2 | e j(q1+q 2) F = |F1 | |F2 或 | q1+q2 F = q1-q2 F1 F2 = |F1 | |F2 | '若两个复数相等 F1 = F2 则必须是 |F1 | = |F2 |,q1=q2 或是 a1 = a2, jb1= jb2 乘(除)法运算满足模相乘(除),辐角相加(减)

复数乘、除的图解 F=FF F F |F2F1 02 F F F 02/ F- F F2 0=01+02 F2 00 0102 0=01-02 +1 +1 乘:F的模被放 ©除:F的模被缩 大F2倍,辐角逆 小F2倍,辐角顺 时针旋转0,。 时针旋转02。 6
6 复数乘、除的图解 F乘: F1的模被放 大|F2 |倍,辐角逆 时针旋转q2 。 F除: F1的模被缩 小|F2 |倍,辐角顺 时针旋转q2 。 +j o +1 q1 F1 F2 q2 |F2 |F1 q2 F=F1F2 q=q1+q2 q1 F1 F2 q2 F1 |F2 | q2 F= F1 F2 q=q1-q2 +j o +1

3.旋转因子ej0 电旋转因子ei0=1∠0是一个模 等于1,辐角为0的复数。 任意一个复数A=|Aea乘以 e0,等于把A逆时针旋转0 +1 角度,而模A保持不变。 e受=j AXj=jA,等于把A 都是旋 逆时针旋转90°。 转因子 ejπ=-1 兰4,等于把顺 时针旋转90°
7 3. 旋转因子e jq G 旋转因子 e jq =1∠q是一个模 等于1,辐角为q的复数。 A 任意一个复数A=|A|e jqa乘以 e jq ,等于把A逆时针旋转q 角度,而模|A|保持不变。 +j o +1 A qa Ae jq q 都是旋 转因子 A×j = jA,等于把 A 逆时针旋转90 o 。 = -jA,等于把 A顺 A j 时针旋转90 o 。 e p 2 = j j e p 2 = -j -j e jp = -1

§8-2正弦量 。电路中按正弦规律变 ②电机、变压器等电气设 化的电压或电流,统 备,在正弦交流电下具 称正弦量。 有较好的性能; ®研究正弦电路的意义 ③正弦量对时间的导数、 是正弦交流电有很多 积分、几个同频率正弦 优点,使它应用广泛。 量的加减,其结果仍是 例如: 同频率的正弦量,这不 ①可以根据需要,利用 仅使电路的分析计算变 变压器方便地把正弦 得简单,而且其结果还 电压升高或降低: 可以推广到非正弦周期 电流电路中
8 §8-2 正弦量 F电路中按正弦规律变 化的电压或电流,统 称正弦量。 C 研究正弦电路的意义 是正弦交流电有很多 优点,使它应用广泛。 例如: ①可以根据需要,利用 变压器方便地把正弦 电压升高或降低; ②电机、变压器等电气设 备,在正弦交流电下具 有较好的性能; ③正弦量对时间的导数、 积分、几个同频率正弦 量的加减,其结果仍是 同频率的正弦量,这不 仅使电路的分析计算变 得简单,而且其结果还 可以推广到非正弦周期 电流电路中

正弦量的时域表达式有两种形式 i=Imc0s(ot什p) i=Isin(ot什p) 也称为瞬时值表达式 分析时不可混用,以免发生相位错误。 采用的形式以教材为准: i=Imcos(o+)u=Uncos(ot+)
9 正弦量的时域表达式有两种形式 i = Imcos(wt+fi) i = Imsin(wt+fi) 也称为瞬时值表达式 分析时不可混用,以免发生相位错误。 采用的形式以教材为准: i = Imcos(wt+fi) u = Umcos(wt+fu)
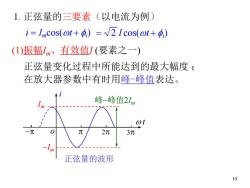
1.正弦量的三要素(以电流为例) i=Imcos(ot+)=2Icos(ot+) (1)振幅Lm、有效值I(要素之一) 正弦量变化过程中所能达到的最大幅度; 在放大器参数中有时用峰-峰值表达。 峰-峰值2Lm ot 元 2元 3元 正弦量的波形 10
10 1. 正弦量的三要素(以电流为例) (1)振幅Im、有效值I (要素之一) o i wt -p p 2p 3p 正弦量的波形 Im-Im 在放大器参数中有时用峰-峰值表达。 峰-峰值2Im 正弦量变化过程中所能达到的最大幅度 ; i = Imcos(wt + fi) = 2 I cos(wt + fi)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《电路》课程教学资源(PPT课件讲稿)第9章 正弦稳态电路分析.ppt
- 《电路》课程教学资源(PPT课件讲稿)第10章 含有耦合电感的电路.ppt
- 《电路》课程教学资源(PPT课件讲稿)第11章 电路的频率响应.ppt
- 《电路》课程教学资源(PPT课件讲稿)第12章 三相电路.ppt
- 《电路》课程教学资源(PPT课件讲稿)第13章 非正弦周期电流电路和信号的频谱.ppt
- 《电路》课程教学资源(PPT课件讲稿)第14章 线性动态电路的复频域分析.pdf
- 《电路》课程教学资源(PPT课件讲稿)第15章 电路方程的矩阵形式.pdf
- 《电路》课程教学资源(PPT课件讲稿)第16章 二端口网络.ppt
- 《电路》课程教学资源(PPT课件讲稿)第17章 非线性电路简介.pdf
- 《电路》课程教学大纲.pdf
- 《电路》课程教学课件(PPT讲稿)第1章 电路模型及定律(山东理工大学:王艳萍).ppt
- 《电路》课程教学课件(PPT讲稿)第2章 电阻电路的等效变换.ppt
- 《电路》课程教学课件(PPT讲稿)第3章 电阻电路的一般分析.ppt
- 《电路》课程教学课件(PPT讲稿)第4章 电路定理.ppt
- 《电路》课程教学课件(PPT讲稿)第5章 含有运算放大器的电阻电路.ppt
- 《电路》课程教学课件(PPT讲稿)第6章 储能元件.ppt
- 《电路》课程教学课件(PPT讲稿)第7章 一阶电路和二阶电路的时域分析.ppt
- 《电路》课程教学课件(PPT讲稿)第8章 相量法.ppt
- 《电路》课程教学课件(PPT讲稿)第9章 正弦稳态电路分析.ppt
- 《电路》课程教学课件(PPT讲稿)第10章 含有耦合电感的电路.pdf
- 《电路》课程教学资源(PPT课件讲稿)第7章 一阶电路和二阶电路的时域分析.ppt
- 《电路》课程教学资源(PPT课件讲稿)第6章 储能元件.pdf
- 《电路》课程教学资源(PPT课件讲稿)第5章 含有运算放大器的电阻电路.pdf
- 《电路》课程教学资源(PPT课件讲稿)第4章 电路定理.ppt
- 《电路》课程教学资源(PPT课件讲稿)第3章 电阻电路的一般分析.ppt
- 《电路》课程教学资源(PPT课件讲稿)第2章 电阻电路的等效变换.ppt
- 《电路》课程教学资源(PPT课件讲稿)第1章 电路模型及定律.ppt
- 《电路》课程教学资源(教案讲义)第10章 含有耦合电感的电路.doc
- 《电路》课程教学资源(教案讲义)第8章 相量法.doc
- 《电路》课程教学资源(教案讲义)第7章 一阶电路和二阶电路的时域分析.doc
- 《电路》课程教学资源(教案讲义)第3章 电阻电路的一般分析.doc
- 《电路》课程教学资源(教案讲义)第2章 电阻电路的等效变换.doc
- 《电路》课程教学资源(教案讲义)第1章 电路模型及定律.doc
- 《电路》课程教学资源(A)课程总复习.ppt
- 《电路》课程教学实验指导书(共十个实验).pdf
- 《电路》课程教学资源(学习资料)电路常见问题.doc
- 《电路》课程教学资源(A)综合复习_电路试卷(二)答案.pdf
- 《电路》课程教学资源(A)综合复习_电路试卷(二)试题.pdf
- 《电路》课程教学资源(A)综合复习_电路试卷(一)答案.pdf
- 《电路》课程教学资源(A)综合复习_电路试卷(一)试题.pdf
