《电路》课程教学资源（教案讲义）第10章 含有耦合电感的电路

电路A教案 书十章舍有病合电感电路 第十章、含有擱合电感电路 §10-1互感 一、互感 两个靠得很近的电感线圈之间有磁的耦合，当线圈1中通电流1时，不仅在线圈 1中产生磁通φ1，同时，有部分磁通21穿过临近线圈2，同理，若在线圈2中通电 流2时，不仅在线圈2中产生磁通φ22，同时，有部分磁通φ12穿过线圈1，p12和p2 称为互感磁通。定义互磁链： 912=W1φ12 21=N2p21 当周围空间是各向同性的线性磁介质时，磁通链与产生它的施感电流成正 比，即有自感磁通链： 911=L3 92=L212 互感磁通链： 912=M22921=M2 上式中M2和M1称为互感系数，单位为(H)。当两个线圈都有电流 时，每一线圈的磁链为自磁链与互磁链的代数和： 1=11土w2=L土M12 2=W22±g21=L,i2±M2 需要指出的是： 1)M值与线圈的形状、几何位置、空间媒质有关，与线圈中的电流无关，因 此，满足M12=M1=M 2)自感系数L总为正值，互感系数M值有正有负。正值表示自感磁链与互 感磁链方向一致，互感起增助作用，负值表示自感磁链与互感磁链方向相反，互感起 削弱作用。 二、耦合因数 工程上用耦合因数k来定量的描述两个耦合线圈的耦合紧密程度，定义 第1页共14页

电路 A 教案 第十章 含有耦合电感电路 第 1 页 共 14 页 §10－1 互感 一、互感 两个靠得很近的电感线圈之间有磁的耦合，当线圈 1 中通电流 i1 时，不仅在线圈 1 中产生磁通 φ11，同时，有部分磁通 φ21 穿过临近线圈 2，同理，若在线圈 2 中通电 流 i2 时，不仅在线圈 2 中产生磁通 φ22，同时，有部分磁通 φ12 穿过线圈 1，φ12 和 φ21 称为互感磁通。定义互磁链： ψ12 = N1φ12 ψ21 = N2φ21 当周围空间是各向同性的线性磁介质时，磁通链与产生它的施感电流成正 比，即有自感磁通链： 互感磁通链： 上式中 M12 和 M21 称为 互感系数，单位为（H）。 当两个线圈都有电流 时，每一线圈的磁链为自磁链与互磁链的代数和： 需要指出的是： １）M 值与线圈的形状、几何位置、空间媒质有关，与线圈中的电流无关，因 此，满足 M 12 =M21 =M ２）自感系数 L 总为正值，互感系数 M 值有正有负。正值表示自感磁链与互 感磁链方向一致，互感起增助作用，负值表示自感磁链与互感磁链方向相反，互感起 削弱作用。 二、耦合因数 工程上用耦合因数 k 来定量的描述两个耦合线圈的耦合紧密程度，定义

电路A教金 第十幸分有妈合电感电落 一般有： k= M M(M)(M) gw21三1 当k=1称全耦合，没有漏磁，满足11=21,22=12。 三、耦合电感上的电压、电流关系 根据电磁感应定律和楞次定律得每个线圈两端的电压为： 4==u±=Lk士M dtdtdt dt 密-尝±警6尝± dt 即线圈两端的电压均包含自感电压和互感电压。 在正弦交流电路中，其相量形式的方程为 立1=ja4i1±jMi2 立2=±jMi1+jawL,2 注意：当两线圈的自感磁链和互感磁链方向一致时，称为互感的增助”作用， 互感电压取正：否则取负。以上说明互感电压的正、负： (1)与电流的参考方向有关。 (2)与线圈的相对位置和绕向有关。 四、互感线图的同名端 同名端：当两个电流分别从两个线圈的对应端子同时流入或流出时，若产生的 磁通相互增强，则这两个对应端子称为两互感线圈的同名端，用小圆点或星号等符号 标记。 注意：当有多个线圈之间存在互感作用时，同名端必须两两线圈分别标定。 根据同名端的定义可以得出确定同名端的方法为： ()当两个线圈中电流同时流入或流出同名端时，两个电流产生的磁场将相互增 强。 (②)当随时间增大的时变电流从一线圈的一端流入时，将会引起另一线圈相应同名端 的电位升高。 第2页共14页

电路 A 教案 第十章 含有耦合电感电路 第 2 页 共 14 页 一般有： 当 k =1 称全耦合，没有漏磁，满足 Φ11 =Φ21 ，Φ22 =Φ12。 三、耦合电感上的电压、电流关系 根据电磁感应定律和楞次定律得每个线圈两端的电压为： 即线圈两端的电压均包含自感电压和互感电压。 在正弦交流电路中，其相量形式的方程为 注意： 当两线圈的自感磁链和互感磁链方向一致时，称为互感的“增助”作用， 互感电压取正；否则取负。以上说明互感电压的正、负： （1）与电流的参考方向有关。 （2）与线圈的相对位置和绕向有关。 四、互感线圈的同名端 同名端: 当两个电流分别从两个线圈的对应端子同时流入或流出时，若产生的 磁通相互增强，则这两个对应端子称为两互感线圈的同名端，用小圆点或星号等符号 标记。 注意：当有多个线圈之间存在互感作用时，同名端必须两两线圈分别标定。 根据同名端的定义可以得出确定同名端的方法为： (1)当两个线圈中电流同时流入或流出同名端时，两个电流产生的磁场将相互增 强。 (2) 当随时间增大的时变电流从一线圈的一端流入时，将会引起另一线圈相应同名端 的电位升高

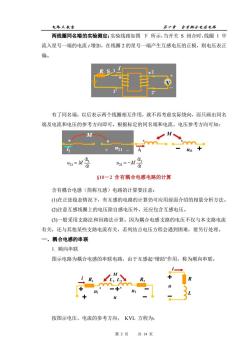
电路A教金 弟十率合有妈合电感电落 两线圈同名端的实验测定：实验线路如图下所示，当开关S闭合时，线圈1中 流入星号一端的电流1增加，在线圈2的星号一端产生互感电压的正极，则电压表正 偏。 有了同名端，以后表示两个线圈相互作用，就不再考虑实际绕向，而只画出同名 端及电流和电压的参考方向即可。根据标定的同名端和电流、电压参考方向可知： M +21- =登 S10一2含有耦合电感电路的计算 含有耦合电感（简称互感）电路的计算要注意： ()在正弦稳态情况下，有互感的电路的计算仍可应用前面介绍的相量分析方法。 (2)注意互感线圈上的电压除自感电压外，还应包含互感电压。 (3)一般采用支路法和回路法计算。因为耦合电感支路的电压不仅与本支路电流 有关，还与其他某些支路电流有关，若列结点电压方程会遇到困难，要另行处理。 一、耦合电感的串联 1.顺向串联 图示电路为耦合电感的串联电路，由于互感起“增助”作用，称为顺向串联。 按图示电压、电流的参考方向，KVL方程为： 第3页共14页

电路 A 教案 第十章 含有耦合电感电路 第 3 页 共 14 页 两线圈同名端的实验测定：实验线路如图 下 所示，当开关 S 闭合时，线圈 1 中 流入星号一端的电流 i 增加，在线圈 2 的星号一端产生互感电压的正极，则电压表正 偏。 有了同名端，以后表示两个线圈相互作用，就不再考虑实际绕向，而只画出同名 端及电流和电压的参考方向即可。根据标定的同名端和电流、电压参考方向可知： §10－2 含有耦合电感电路的计算 含有耦合电感（简称互感）电路的计算要注意： (1)在正弦稳态情况下，有互感的电路的计算仍可应用前面介绍的相量分析方法。 (2)注意互感线圈上的电压除自感电压外，还应包含互感电压。 (3)一般采用支路法和回路法计算。因为耦合电感支路的电压不仅与本支路电流 有关，还与其他某些支路电流有关，若列结点电压方程会遇到困难，要另行处理。 一、耦合电感的串联 1. 顺向串联 图示电路为耦合电感的串联电路，由于互感起“增助”作用，称为顺向串联。 按图示电压、电流的参考方向， KVL 方程为：

电路A教拿 弟十率今有辆合电感电路 =R+乙+M+L,+M座+R =(R+R+亿，+五+2M是=+L是 根据上述方程可以给出无互感等效电路。等效电路的参数为： R=R+R L=L+L,+2M 2.反向串联 图示的耦合电感的串联电路，由于互感起“削弱”作用，称为反向串联。按图示电 压、电流的参考方向，KVL方程为： u=R+马是-M票+，是-M+R风 =(民+R+G+,-20毫=冠+L毫 + 0+ 无互感（去耦）等效电路。但等效电路的参数为： R=+ L=L+L-2M 注意： ()互感不大于两个自感的算术平均值，整个电路仍呈感性，即满足关系： L=4+5-2M≥0M≤4+) (2)根据上述讨论可以给出测量互感系数的方法：把两线圈顺接一次，反接一 M=顺复 次，则互感系数为： 二、耦合电感的并联 1.同侧并联：同名端连接在同一个结点上，称为同侧串联。 根据KVL得同侧并联电路的方程为 =4壹+受=6是+盘 由于i=1+2 解得4，i的关系： =华盟 第4页共14页

电路 A 教案 第十章 含有耦合电感电路 第 4 页 共 14 页 根据上述方程可以给出无互感等效电路。等效电路的参数为： 2. 反向串联 图示的耦合电感的串联电路，由于互感起“削弱”作用，称为反向串联。按图示电 压、电流的参考方向，KVL 方程为： 无互感（去耦）等效电路。但等效电路的参数为： 注意： （1）互感不大于两个自感的算术平均值，整个电路仍呈感性，即满足关系： （2）根据上述讨论可以给出测量互感系数的方法：把两线圈顺接一次，反接一 次，则互感系数为： 二、耦合电感的并联 1. 同侧并联：同名端连接在同一个结点上，称为同侧串联。 根据 KVL 得同侧并联电路的方程为 由于 i = i1 + i2 解得 u , i 的关系：

电路A教案 弟十率合有妈合电感电落 其等效电感为： 鼎 2.异侧并联：耦合电感的异名端连接在同一个结点上，故称为异侧并联。 此时电路的方程为： u=是-M÷u=是-M当 考虑到：i=+b 解得w,i的关系： 盟 (LL,-M) 无互感等效电路，其等效电感为： L4-+2+2☑ 三、耦合电感的T型去耦等效 如果耦合电感的2条支路各有一端与第三条支路形成一个仅含三条支路的共同 结点，称为耦合电感的T型联接。显然耦合电感的并联也属于T型联接。 1.同名端为共端的T型去耦等效 同名端为共端的T型联接。根据所标电压、电流的参考方向得： Un=jal h+ja ia=jo(L-M)in+jaui Un=jal ia+jai=jo(L-M)ia+jMi 2.异名端为共端的T型去耦等效 异名端为共端的T型联接。根据所标电压、电流的参考方向得： Un=jaL i-jaMin=jo(L+M)in-jaMi Un jal,in-jal in=jo(L+M)ia-jaM i 注意：T型去耦等效电路中3条支路的等效电感分别为： 支路3：乙，=士M（同侧取“+”异侧取一) 支路1：=马干M 支路2：=L2干M 例：求图(a)、(b)所示电路的等效电感乙。 解：(a)图中4H和6H电感为T型结构，应用T型去耦等效得图(c)电路。 则等效电感为： 弟5贝共14贝

电路 A 教案 第十章 含有耦合电感电路 第 5 页 共 14 页 其等效电感为： 2. 异侧并联：耦合电感的异名端连接在同一个结点上，故称为异侧并联。 此时电路的方程为： 考虑到：i = i1 + i2 解得 u , i 的关系： 无互感等效电路，其等效电感为： 三、耦合电感的 T 型去耦等效 如果耦合电感的 2 条支路各有一端与第三条支路形成一个仅含三条支路的共同 结点，称为耦合电感的 T 型联接。显然耦合电感的并联也属于 T 型联接。 1. 同名端为共端的 T 型去耦等效 同名端为共端的 T 型联接。根据所标电压、电流的参考方向得： 2. 异名端为共端的 T 型去耦等效 异名端为共端的 T 型联接。根据所标电压、电流的参考方向得： 注意：T 型去耦等效电路中 3 条支路的等效电感分别为： 支路 3 ： （同侧取“ + ”，异侧取“—”） 支路 1 ： 支路 2 ： 例：求图（a）、（b）所示电路的等效电感 。 解：（a）图中 4H 和 6H 电感为 T 型结构，应用 T 型去耦等效得图（c）电路。 则等效电感为：

电路A教金 书十華分有妈合电感电落 M-3H 4H 3H 0.51H SM1H了 图(a) 图(b) 9H 3H 05H 图(c) 图(d) L=2+05+7+9x(-3=95-45=5H 9-3 (b)图中5H和6H电感为同侧相接的T型结构，2H和3H电感为异侧相接的T 型结构，应用T型去耦等效得图(d)电路。则等效电感为： L=1+3+3x2+0-6H 2+4+3 §10一3耦合电感的功率 当耦合电感中的施感电流变化时，将出现变化的磁场，从而产生电场（互感电压）， 耦合电感通过变化的电磁场进行电磁能的转换和传输，电磁能从耦合电感一边传输到 另一边。由下图所示，电路的方程为： +山鲁+N受= M受+R4+会=0 L2 第1式乘，第2式乘，得到耦合电感解时 功率方程为： 第6页共14页

电路 A 教案 第十章 含有耦合电感电路 第 6 页 共 14 页 图（ c ） 图（ d ） （b）图中 5H 和 6H 电感为同侧相接的 T 型结构，2H 和 3H 电感为异侧相接的 T 型结构，应用 T 型去耦等效得图（d）电路。则等效电感为： §10－3 耦合电感的功率 当耦合电感中的施感电流变化时，将出现变化的磁场，从而产生电场（互感电压）， 耦合电感通过变化的电磁场进行电磁能的转换和传输，电磁能从耦合电感一边传输到 另一边。由下图所示，电路的方程为： 0 2 2 2 2 1 1 2 1 1 1 + + = + + = dt di R i L dt di M u dt di M dt di R i L s 第 1 式乘 1 i ，第 2 式乘 2 i ，得到耦合电感瞬时 功率方程为： 图（a） 图（b） us + - i1 R1 R2 L2 · L1 · M i2

电路A教金 弟十率合有妈合电感电蓉 风4+叠+M费-4 M度+风6+6告-0 当电路中的电压、电流为同频率正弦量时，两个线圈的复功率分别为： 两个互感电压耦合的复功率为虚部同号，实部异号，这是耦合电感本身的电磁特 性所决定的。 耦合功率中的有功功率相互异号，表明有功功率从一个端口进入，必从另一个端 口输出。这是互感M非耗能特性的体现。 耦合功率中的无功功率同号，表明两个互感电压耦合功率中的无功功率对两个耦 合线圈的影响、特性是相通的。当M起同向耦合作用时，它的储能特性与电感相同， 使耦合电感的磁能增加。当M起反向耦合作用时，它的储能特性与电容相同，使耦 合电感的磁能减少。 §10一4变压器原理 变压器由两个具有互感的线圈构成，一个线圈接向电源，另一线圈接向负载。变 压器是通过互感来实现从一个电路向另一个电路传输能量或信号的器件。当变压器线 圈的芯子为非铁磁材料时，称空心变压器。 一、空心变压器电路 图示电路为空心变压器的电路模型，与电源相接的回路称为原边回路（或初级回 路)，与负载相接的回路称为副边回路（或次级回路）。 二、分析方法 1.方程法分析：在正弦稳态情况下，电路的回路方程为： (风+jmi-jaM i2=tis -jaMi+(R3+j@L2+Z)i2=0 第7页共14页

电路 A 教案 第十章 含有耦合电感电路 第 7 页 共 14 页 0 2 2 2 2 2 2 1 2 1 2 1 1 1 1 2 1 1 + + = + + = dt di R i i L dt di Mi u i dt di i M dt di R i L i s 当电路中的电压、电流为同频率正弦量时，两个线圈的复功率分别为： 两个互感电压耦合的复功率为虚部同号，实部异号，这是耦合电感本身的电磁特 性所决定的。 耦合功率中的有功功率相互异号，表明有功功率从一个端口进入，必从另一个端 口输出。这是互感 M 非耗能特性的体现。 耦合功率中的无功功率同号，表明两个互感电压耦合功率中的无功功率对两个耦 合线圈的影响、特性是相通的。当 M 起同向耦合作用时，它的储能特性与电感相同， 使耦合电感的磁能增加。当 M 起反向耦合作用时，它的储能特性与电容相同，使耦 合电感的磁能减少。 §10－4 变压器原理 变压器由两个具有互感的线圈构成，一个线圈接向电源，另一线圈接向负载。变 压器是通过互感来实现从一个电路向另一个电路传输能量或信号的器件。当变压器线 圈的芯子为非铁磁材料时，称空心变压器。 一、空心变压器电路 图示电路为空心变压器的电路模型，与电源相接的回路称为原边回路（或初级回 路），与负载相接的回路称为副边回路（或次级回路）。 二、分析方法 1. 方程法分析：在正弦稳态情况下，电路的回路方程为：

电路A教拿 弟十率合有病合电感电恐 令乙4=月+j四马称为原边回路阻抗，乙知=凡+J0L,+乙称为副边回路阻 抗。则上述方程简写为： 2uh-jal in=Us -ja h+Znia=0 从上列方程可求得原边和副边电流 3,+ i=ja is ja i's 1 名2如+a7 Z11 2.等效电路法分析：等效电路法实质上是在方程分析法的基础上找出求解的某 些规律，归纳总结成公式，得出等效电路，再加以求解的方法。 首先讨论原边等效电路。令上述原边电流的分母为： 2,=2+a-2+2, U: 则原边电流为： 根据上式可以画出原边等效电路如下图所示。上式中的Z:称为引入阻抗（或反 映阻抗)，是副边回路阻抗通过互感反映到原边的等效阻抗，它体现了副边回路的存 在对原边回路电流的影响。从物理意义讲，虽然原、副边没有电的联系，但由于互 感作用使闭合的副边产生电流，反过来这个电流又影响原边电流电压。 把引入阻抗Z展开得： 3=(a) 02M2 0'M'Rg-j Ra+jxaR品+Xa 'M'X2=Ry+jXy 品+Xa 上式表明： 第8页共14页

电路 A 教案 第十章 含有耦合电感电路 第 8 页 共 14 页 令 称为原边回路阻抗， 称为副边回路阻 抗。则上述方程简写为： 从上列方程可求得原边和副边电流 2. 等效电路法分析：等效电路法实质上是在方程分析法的基础上找出求解的某 些规律，归纳总结成公式，得出等效电路，再加以求解的方法。 首先讨论原边等效电路。令上述原边电流的分母为： 则原边电流为： 根据上式可以画出原边等效电路如下图所示。上式中的 Zf 称为引入阻抗（或反 映阻抗），是副边回路阻抗通过互感反映到原边的等效阻抗，它体现了副边回路的存 在对原边回路电流的影响。 从物理意义讲，虽然原、副边没有电的联系，但由于互 感作用使闭合的副边产生电流，反过来这个电流又影响原边电流电压。 把引入阻抗 Zf 展开得： 上式表明：

电路A教金 弟十来合有妈合电感电蘑 Ru= @MR (1)引入电阻 +X”不仅与次级回路的电阻有关，而且与次级回路 的电抗及互感有关。 @MX Xy = (2)引入电抗 +X拉的负号反映了引入电抗与付边电抗的性质相 反。 可以证明引入电阻消耗的功率等于副边回路吸收的功率。根据副边回路方程得： jch=2ni 方程两边取模值的平方：（幻程=（码+场）片 从中得： 月路-民片-月 应用同样的方法分析方程法得出的副边电流表达式。令 ija Us-joMh Z11 Z-24+a@0-24+Z i2= U a+石2+@7 Zu 根据上式可以画出副边等效电路，上式中的称为原边回路对副边回路的引入 阻抗，它与Z有相同的性质。应用戴维宁定理也可以求得空心变压器副边的等效电 路。 3.去耦等效法分析：对空心变压器电路进行T型去耦等效，变为无互感的电路， 再进行分析。 例：图()为空心变压器电路，己知电源电压Us=20V,原边引入阻抗，☑ =10-j102,求：负载阻抗Z并求负载获得的有功功率。 解：图(a)的原边等效电路如图(b)所示，引入阻抗为： 名=话z0=10-10 第9页共14页

电路 A 教案 第十章 含有耦合电感电路 第 9 页 共 14 页 （1）引入电阻 不仅与次级回路的电阻有关，而且与次级回路 的电抗及互感有关。 （2）引入电抗 的负号反映了引入电抗与付边电抗的性质相 反。 可以证明引入电阻消耗的功率等于副边回路吸收的功率。根据副边回路方程得： 方程两边取模值的平方： 从中得： 应用同样的方法分析方程法得出的副边电流表达式。令 根据上式可以画出副边等效电路，上式中的 Z2f 称为原边回路对副边回路的引入 阻抗，它与 Z1f 有相同的性质。应用戴维宁定理也可以求得空心变压器副边的等效电 路。 3. 去耦等效法分析：对空心变压器电路进行 T 型去耦等效，变为无互感的电路， 再进行分析。 例：图（a）为空心变压器电路，已知电源电压 US=20V，原边引入阻抗，Zl =10–j10Ω，求：负载阻抗 ZX 并求负载获得的有功功率。 解：图（a）的原边等效电路如图（b）所示，引入阻抗为：

电路A教第 书十華分有妈合电感电落 2。 10+5100 Zr10j100 图(a) 图(b) 2,=100-10=20.0-10=0.2-j980】 4 从中解得： 200 此时负载获得的功率等于引入电阻消耗的功率，因此： 20 P=R=（04oR=10w 注意：电路实际处于最佳匹配状态，即 名=2云，P=器-10w 例：已知图(a)空心变压器电路参数为：L1=3.6H,L2=0.06,M=0.465H,R1=202 及-008n,R=42n,=314ads,立=15∠0°V,求：原、副边电流，方. 11 0 图(a) s0 图(b) 图(c) 解法1：应用图(b)所示的原边等效电路，得： Z1=R+jL1=20+j1130.42 Z2=R2+R,+jmL2=42.08+j18852 五要6r6z内-2an 1462 第10页共14页

电路 A 教案 第十章 含有耦合电感电路 第 10 页 共 14 页 图 （ a ） 图 （ b ） 从中解得： 此时负载获得的功率等于引入电阻消耗的功率，因此： 注意：电路实际处于最佳匹配状态，即 例：已知图（a）空心变压器电路参数为：L1=3.6H，L2=0.06H，M =0.465H，R1=20Ω， R2=0.08Ω，RL=42Ω，ω=314rad/s， ，求：原、副边电流 。 图（a） 图（b） 图（c） 解法 1：应用图（b）所示的原边等效电路，得：