《电路》课程教学资源（A）综合复习_电路模拟题（下）

一、电路如图， usi(1)=3e-'(t)V ☐h2 42()=e2e(t)V,试求电流i2()。 1F 12 0.5H 解：1()和42（①）的象函数为 0.22 U16)=3 7 U2)= S+2 s域电路的网孔电流方程为： (日+0.2)1)-0.25)=3 -0.211(+(0.5s+1.2)12()=- 12(s) S+2 解之： 4s2-10 12(S)= 求反变换： (S+1)(S+2)(S+3)(s+4) i2(t)=(-e-3e-2+13e-31-9e4c(t)V 用部分分式展开： 3)=1 +-313 +9 S+1S+2S+3S+4

一、电路如图， + 1F - us1 i1 i2 1W 0.5H + - 0.2W us2 us1(t)=3e-te(t)V us2(t)=e -2te(t)V， 试求电流i2 (t)。 解：us1(t)和 us2(t) 的象函数为 Us1(s) = s+1 3 Us2(s) = s+2 1 s域电路的网孔电流方程为： s 1 + 0.2 I1 (s) - 0.2 I2 (s) = s+1 3 - 0.2 I1 (s) + (0.5s+1.2) I2 (s) = - s+2 1 解之： I2 (s) = (s+1) (s+2) (s+3) (s+4) 4s 2 - 10 用部分分式展开： I2 (s) = s+1 -1 + s+2 -3 + s+3 13 + s+4 -9 求反变换： i2 (t) = (-e -t-3e -2t+13e -3t-9e -4t ) e(t) V 1/s + - Us1(s) 1 0.5s + - 0.2 Us2(s) I1 (s) I2 (s) I1 (s) I2 (s)

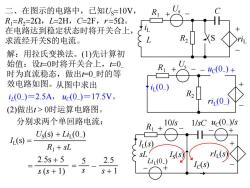
二、在图示的电路中，已知Us=10V, R1=R2=22,L=2H,C=2F,r=52。 在电路达到稳定状态时将开关合上， 求流经开关$的电流。 Q 解：用拉氏变换法。()先计算初 始值：设仁0时将开关合上，仁0 R1+ 时为直流稳态，做出=0时的等 .-uc(0 效电路如图。从图中求出 i(0) i(0)=2.5A,uc(0)=17.5V. R2 i(0)） (2)做出t>0时运算电路图。 分别求两个单回路电流： R 10/s1/sCuc(0)/s Us(s)+LiL(O) I(S)= R+SL 2.5s+5 -5 2.5 Is© rh(5) s(s+1) S S+1 Ic(s)

二、在图示的电路中，已知US=10V， R1=R2=2Ω，L=2H，C=2F，r =5Ω。 在电路达到稳定状态时将开关合上， 求流经开关S的电流。 + - riL C R2 S + - R Us 1 iL L + - R2 + - R Us 1 iL (0- ) riL (0- ) uC (0- - ) + 解：用拉氏变换法。(1)先计算初 始值：设t=0时将开关合上，t=0- 时为直流稳态，做出t=0-时的等 效电路如图。 iL (0- )＝2.5A， uC(0- )＝17.5V。 (2)做出t > 0时运算电路图。 从图中求出 IL (s) = US (s) + LiL (0- ) R1 + sL = 2.5s + 5 s (s + 1) = s 5 - s + 1 2.5 分别求两个单回路电流： + - rIL (s) 1/sC + - 10/s R1 IL (s) sL uC(0- )/s - + IS (s) IC (s) - + LiL (0- )

(s)= 5 2.5 S S+1 =sC[r1付-e0) 25 =-10+ S+1 R uc(0)+ 4)=s-1=10+ 27.5 +1 (0) 取拉氏反变换得： is(t)=[(5-27.5e)ε(t)+10δ(t)]A 10/s1/sCuc(0_)/s 由于电路中有CCVS与C构成 回路，故在换路瞬间电容电 压跃变，出现了冲激电流。 Li(0) Is(s) Ic(s)

IL (s) = s 5 - s + 1 2.5 IC(s) = sC [ r IL (s) - s uC(0- ) ] = - 10 + s + 1 25 IS (s) = IL (s) - IC (s) = 10 + s 5 - s + 1 27.5 取拉氏反变换得： iS (t) = [(5 - 27.5 e-t ) e(t) +10 d(t) ] A 由于电路中有CCVS与C构成 回路，故在换路瞬间电容电 压跃变，出现了冲激电流。 + - riL C R2 S + - R Us 1 iL L + - R2 + - R Us 1 iL (0- ) riL (0- ) uC (0- - ) + + - rIL (s) 1/sC + - 10/s R1 IL (s) sL uC(0- )/s - + IS (s) IC (s) - + LiL (0- )

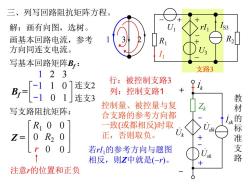
三、列写回路阻抗矩阵方程。 解：画有向图，选树。 画基本回路电流，参考 方向同连支电流。 写基本回路矩阵Br: 123 支路3 1 0连支2 行：被控制支路3 列：控制支路1 9k 101连支3 控制量、被控量与复 写支路阻抗矩阵： 合支路的参考方向都 R100 一 致（或都相反）时取 Z= 0R20 正，否则取负。 U r 0 若rl的参考方向与题图 教材的标准支路 相反，则Z中就是(-)。 注意的位置和正负

三、列写回路阻抗矩阵方程。 I1 U1 R1 R2 - + rI1 + - U3 IS3 + - 解：画有向图，选树。 画基本回路电流，参考 1 3 2 方向同连支电流。 支路3 写基本回路矩阵Bf ： -1 1 0 -1 0 1 Bf = 1 2 3 连支2 连支3 写支路阻抗矩阵： Z = R1 0 R2 0 0 0 0 r 0 注意r的位置和正负 控制量、被控量与复 合支路的参考方向都 一致(或都相反)时取 正，否则取负。 Zk - + . Usk . Isk . Ik - + . Uk + - . Udk 行：被控制支路3 列：控制支路1 若rI1的参考方向与题图 相反，则Z中就是(-r)。 教 材 的 标 准 支 路

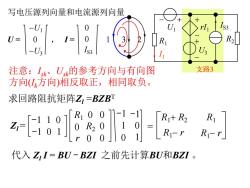
写电压源列向量和电流源列向量 U- 注意：Ik、U的参考方向与有向图 支路3 方向方向)相反取正，相同取负。 求回路阻抗矩阵Z,=BZBT ie91-8 代入Z,I=BU-BZI之前先计算BU和BZI

写电压源列向量和电流源列向量 U = -U1 -U3 0 ， I = 0 0 IS3 注意：Isk、Usk的参考方向与有向图 方向(Ik方向)相反取正，相同取负。 -1 1 0 -1 0 1 R1 0 R2 0 0 0 0 r 0 求回路阻抗矩阵Zl =BZBT Zl = -1 1 0 -1 0 1 = R1+ R2 R1 R1- r R1- r I1 U1 R1 R2 - + rI1 + - U3 IS3 + - 1 3 2 支路3 代入 Zl I = BU - BZI 之前先计算BU和BZI

- R -] 支路3 代入Z,I=BU-BZI得 问：为何1s3不出现 在最后的方程中？ w 答：R1、R2的电流 由电压源决定

BU = -1 1 0 -1 0 1 -U1 -U3 0 = U1 U1 - U3 BZI= 0 0 IS3 -1 1 0 -1 0 1 R1 0 R2 0 0 0 0 r 0 = 0 0 代入 Zl I = BU - BZI 得 R1+ R2 R1 R1- r R1- r Il2 Il3 = U1 U1 - U3 I1 U1 R1 R2 - + rI1 + - U3 IS3 + - 1 3 2 支路3 问：为何IS3不出现 在最后的方程中？ 答：R1、R2的电流 由电压源决定

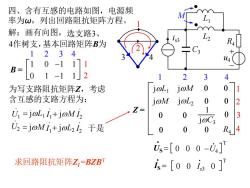
四、含有互感的电路如图，电源频 率为ω，列出回路阻抗矩阵方程。 解：画有向图，选支路3、 4作树支，基本回路矩阵B为 123.4 0-1 111 )1-112 2 3 为写支路阻抗矩阵Z,考虑 joL joM 0 0 含互感的支路方程为： joM joL 0 0 U=j@L1+j@MI ,Z= 0 3 U2=joMi,+joL22于是 0 R44 Us=[000-0] 求回路阻抗矩阵Z,=BZBT s=[00i30]

四、含有互感的电路如图，电源频 率为ω，列出回路阻抗矩阵方程。 i s3 C3 L2 L1 M R4 + - u4 解：画有向图，选支路3、 3 4 2 1 4作树支，基本回路矩阵B为 B = 1 2 3 4 1 2 1 0 -1 1 0 1 -1 1 为写支路阻抗矩阵Z，考虑 含互感的支路方程为： U1 . = jwL1 I1 . + jwM I2 . U2 . = jwM I1 . + jwL2 I2 . 于是 Z = 1 2 3 4 1 2 3 4 0 0 0 0 0 R4 US = . 0 0 0 -U4 . T IS = . 0 0 Is3 0 . T jwL1 jwM jwM jwL2 0 0 0 0 jwC3 1 0 求回路阻抗矩阵Zl =BZBT

joL j@M 0 -Bz-[0 0-11 joM joL 0 0 0 1-1 0 0 0 0 0 R 11 1/j@M+Ra+joL 1/j@C3+Ra+j@M 1/j@C3+R+joM 1/j@C3+Rs+j@L2 代入Z,i=BUs-Bzis便得回路电流方程的矩阵形式： w 本题的互感也可以用含CCVS的等效电路替代

Zl =BZBT = 0 0 0 0 0 R4 jwL1 jwM jwM jwL2 0 0 0 0 jwC3 1 0 1 0 -1 1 0 1 -1 1 1 0 -1 1 0 1 -1 1 = 1/jwM + R4 + jwL1 1/jwC3 + R4 + jwM 1/jwC3 + R4 + jwM 1/jwC3 + R4 + jwL2 Zl . I = . BUS -BZ . I 代入 S 便得回路电流方程的矩阵形式： 1/jwM + R4 + jwL1 1/jwC3 + R4 + jwM 1/jwC3 + R4 + jwM 1/jwC3 + R4 + jwL2 I1 . I2 . = -U4 . + IS3 . /jwC3 -U4 . + IS3 . /jwC3 本题的互感也可以用含CCVS的等效电路替代

五、某电路的关联矩阵为： 1110 0 其复合 A- 0-1 0 0-1 支路如 00-110 右图： 支路导纳矩阵为Y=diag[1joL1,G2,0,joC4,1/joLs] 支路电压源向量为U=[Us1,0,-U3,0,-Uss]I 支路电流源向量为I=[0,2,s3’0,-s]T 求：1根据关联矩阵画出有向图；单击 2列出支路关系方程；单击 3.推求结点电压方程的矩阵形式；单击 4.画出电路图。单击

五、某电路的关联矩阵为： - + Yk Usk Isk Ik + - A Uk = 1 1 1 0 0 0 -1 0 0 -1 0 0 -1 1 0 支路导纳矩阵为 其复合 支路如 右图： Y = diag [1/jwL1 , G2 , 0, jwC4 , 1/jwL5 ] 支路电流源向量为 IS2 . I = [ 0， ， ，0， - ] T IS3 . IS5 . 求：1.根据关联矩阵画出有向图；单击 2.列出支路关系方程；单击 3.推求结点电压方程的矩阵形式；单击 4.画出电路图。单击 支路电压源向量为 U = [ ，0，- ， 0，- ] T US1 . US3 . US5

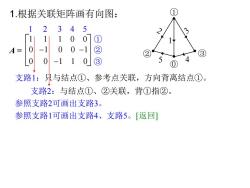
1.根据关联矩阵画有向图： 1 23 45 10 1 1 00 ① A= 0 -1 0 0-1 ② 2 0 -11 0③ 支路1： 央与结点①、参考点关联，方向背离结点①。 支路2：与结点①、②关联，背①指②。 参照支路2可画出支路3。 参照支路1可画出支路4、支路5。「返回]

支路1：只与结点①、参考点关联，方向背离结点①。 A = 1 1 1 0 0 0 -1 0 0 -1 0 0 -1 1 0 1 2 3 4 5 ① ② ③ 支路2：与结点①、②关联，背①指②。 参照支路2可画出支路3。 参照支路1可画出支路4、支路5。[返回] 1.根据关联矩阵画有向图： ③ ① 1 0 ② 5 4