《电路》课程教学资源（PPT课件讲稿）第7章 一阶电路和二阶电路的时域分析

第七章一阶电路和二阶电路的时域分析 内容提要与基本要求 1.换路定则和电路初始值的求法： 2.掌握一阶电路的零输入响应、零状态响应、全响 应的概念和物理意义； 3.会计算和分析一阶动态电路（重点是三要素法）： 4.了解二阶电路零状态响应、零输入响应、全响应 的概念和物理意义； 5.会分析简单的二阶电路； 6.会计算一阶电路的阶跃响应、冲激响应； 7.会用系统法列写简单的状态方程。 1

1 第七章 一阶电路和二阶电路的时域分析 1.换路定则和电路初始值的求法； 2.掌握一阶电路的零输入响应、零状态响应、全响 应的概念和物理意义； 3.会计算和分析一阶动态电路(重点是三要素法)； 4.了解二阶电路零状态响应、零输入响应、全响应 的概念和物理意义； 5.会分析简单的二阶电路； 6.会计算一阶电路的阶跃响应、冲激响应； 7.会用系统法列写简单的状态方程。 内容提要与基本要求

重点 ()动态电路方程的建立和动态电路初始值的确定； (2)一阶电路时间常数的概念与计算； (3)一阶电路的零输入响应和零状态响应： (4)求解一阶电路的三要素法： (⑤)暂态分量（自由分量）和（稳态分量）强制分量概念： (6)二阶电路的零输入、零状态和全响应的概念； (7)二阶电路的方程和特征根、过渡过程的过阻尼、欠 阻尼及临界阻尼的概念及分析： (8)二阶电路的阶跃响应。 2

2 重点 (1)动态电路方程的建立和动态电路初始值的确定； (2)一阶电路时间常数的概念与计算 ； (3)一阶电路的零输入响应和零状态响应； (4)求解一阶电路的三要素法； (5)暂态分量(自由分量)和(稳态分量)强制分量概念； (6)二阶电路的零输入、零状态和全响应的概念； (7)二阶电路的方程和特征根、过渡过程的过阻尼、欠 阻尼及临界阻尼的概念及分析； (8)二阶电路的阶跃响应

难点 (1)应用基尔霍夫定律和电感、电容的元件特性建 立动态电路方程； (2)电路初始条件的概念和确定方法； (3)二阶电路的过阻尼、欠阻尼及临界阻尼放电过 程分析方法和基本物理概念。 与其它章节的联系 本章讨论的仍是线性电路，因此前面讨论的线性 电路的分析方法和定理全部可以用于本章的分析 中。第9章讨论的线性电路的正弦稳态响应就是 动态电路在正弦激励下的稳态分量的求解。 3

3 难点 (1)应用基尔霍夫定律和电感、电容的元件特性建 立动态电路方程； (2)电路初始条件的概念和确定方法； (3)二阶电路的过阻尼、欠阻尼及临界阻尼放电过 程分析方法和基本物理概念。 与其它章节的联系 本章讨论的仍是线性电路，因此前面讨论的线性 电路的分析方法和定理全部可以用于本章的分析 中。第9章讨论的线性电路的正弦稳态响应就是 动态电路在正弦激励下的稳态分量的求解

§7-1动态电路的方程及其初始条件 引言 自然界事物的运动，在一定的条件下有一定的稳 定状态。当条件发生变化时，就要过渡到新的稳定状 态。从一种稳定状态转到另一种新稳定状态时，往往 不能跃变，而是需要一定时间，或者说需要一个过程， 在工程上称过渡过程。 S(t=0) 接通电源，C被充电，C两 端的电压逐渐增长到稳态值 U,即要经历一段时间。 电路中的过渡过程虽然短暂， 在实践中却很重要

4 §7-1 动态电路的方程及其初始条件 S US + - (t=0) + - uC R C + uR - i 引 言 自然界事物的运动，在一定的条件下有一定的稳 定状态。当条件发生变化时，就要过渡到新的稳定状 态。从一种稳定状态转到另一种新稳定状态时，往往 不能跃变，而是需要一定时间，或者说需要一个过程， 在工程上称过渡过程。 接通电源，C 被充电，C 两 端的电压逐渐增长到稳态值 Us ，即要经历一段时间。 电路中的过渡过程虽然短暂， 在实践中却很重要

一、动态电路的基本概念 >含有动态元件(L、C)的电路称为动态电路。描 述动态电路的方程是微分方程。 >全部由线性非时变元件构成的动态申路，其描 述方程是线性常系数微分方程。 >只含一个动态元件(L或C)的电路，其描述方程 是一阶线性常系数微分方程，称一阶申路。 >一阶电路有3种分析方法： 1.经典法 列写电路的微分方程，求解电流和电压。是一种 在时间域中进行的分析方法。 5

5 一、动态电路的基本概念 ➢ 含有动态元件(L、C)的电路称为动态电路。描 述动态电路的方程是微分方程。 ➢ 全部由线性非时变元件构成的动态电路，其描 述方程是线性常系数微分方程。 ➢ 只含一个动态元件(L或C)的电路，其描述方程 是一阶线性常系数微分方程，称一阶电路。 ➢ 一阶电路有3种分析方法： 1. 经典法 列写电路的微分方程，求解电流和电压。是一种 在时间域中进行的分析方法

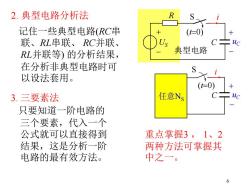
2.典型电路分析法 记住一些典型电路(RC串 (t=0) 联、RL串联、RC并联、 RL并联等)的分析结果， 典型电路 在分析非典型电路时可 以设法套用。 3.三要素法 任意Ns 只要知道一阶电路的 三个要素，代入一个 公式就可以直接得到 重点掌握3,1、2 结果，这是分析一阶 两种方法可掌握其 电路的最有效方法。 中之一。 6

6 2. 典型电路分析法 记住一些典型电路(RC串 联、RL串联、 RC并联、 RL并联等) 的分析结果， 在分析非典型电路时可 以设法套用。 3. 三要素法 只要知道一阶电路的 三个要素，代入一个 公式就可以直接得到 结果，这是分析一阶 电路的最有效方法。 任意NS C uC + - i S (t=0) S US + - (t=0) + - uC R C i 典型电路 重点掌握3 ， 1、2 两种方法可掌握其 中之一

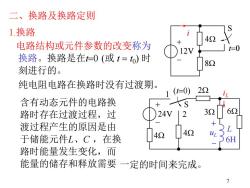
二、换路及换路定则 1换路 电路结构或元件参数的改变称为 12V =0 换路。换路是在=0（或t=o)时 82 刻进行的。 纯电阻电路在换路时没有过渡期。 1(0) 22 含有动态元件的电路换 路时存在过渡过程，过 24V 12 39 渡过程产生的原因是由 42 4Ω2 于储能元件L、C,在换 路时能量发生变化，而 能量的储存和释放需要一定的时间来完成

7 二、换路及换路定则 1.换路 电路结构或元件参数的改变称为 换路。换路是在t=0 (或 t = t0 ) 时 刻进行的。 含有动态元件的电路换 路时存在过渡过程，过 渡过程产生的原因是由 于储能元件L、C ，在换 路时能量发生变化，而 能量的储存和释放需要 S 24V + - (t=0) + L iL 4W 1 4W 2 2W 3W 6H 6W - uL 12V + - i 8W 4W t=0 S 纯电阻电路在换路时没有过渡期。 一定的时间来完成

2.换路定则 线性电容C的电荷g=g6)ic(③d5 以t=。=0作为换路的计时起点：换路前最终时 刻记为t=0_,换路后最初时刻记为t=0+。 在换路前后：90)=90)（⑤ 0_到0瞬间，ic(t)为有限值时，积分为0。 q(0+)=q(O-)C上的电荷不能跃变！ 由g(t)=Cuc()可知，当换路前后C不变时 uc(0)=uc(0_)C两端的电压也不能跃变！ 8

8 2. 换路定则 在换路前后： q(t) = q(t0 ) + t t0 iC (x) dx q(0+ ) = q(0- ) + 0+ 0- iC(x) dx 以t = t0 = 0作为换路的计时起点：换路前最终时 刻记为t = 0-，换路后最初时刻记为t = 0+。 线性电容C的电荷 0-到0+瞬间，iC(t)为有限值时，积分为0。 q(0+ ) = q(0- ) C上的电荷不能跃变！ 由q(t) = C uC(t)可知，当换路前后C不变时 uC(0+ ) = uC(0- ) C两端的电压也不能跃变！

q(0+)=q(0-) uc(0+)=uc(0_） 同理可得： Ψ(0)=Ψ(0)》 L中的磁链不能跃变！ 由平Ψ()=Li()可知，当换路前后L不变时 (0)=i(0) L中的电流也不能跃变！ 换路定则表明 (1)换路瞬间，若电容电流保持为有限值，则电 容电压（电荷）在换路前后保持不变，这是 电荷守恒定律的体现。 (2)换路瞬间，若电感电压保持为有限值，则电 感电流（磁链）在换路前后保持不变。这是 磁链守恒定律的体现。 9

9 Y (0+ ) =Y (0- ) L中的磁链不能跃变！ 由Y (t) = LiL (t) 可知，当换路前后L不变时 iL (0+ ) = iL (0- ) L中的电流也不能跃变！ q(0+ ) = q(0- ) uC(0+ ) = uC(0- ) 同理可得： 换路定则表明 (1)换路瞬间，若电容电流保持为有限值，则电 容电压（电荷）在换路前后保持不变，这是 电荷守恒定律的体现。 (2)换路瞬间，若电感电压保持为有限值，则电 感电流（磁链）在换路前后保持不变。这是 磁链守恒定律的体现

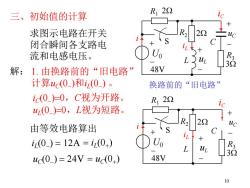
三、初始值的计算 R122 求图示电路在开关 闭合瞬间各支路电 流和电感电压。 解：1.由换路前的“旧电路” 48V 计算uc(0)和iz(0)。 换路前的“旧电路” i(0)=0,C视为开路。 R122 u(0_)=0,L视为短路。 R2 22 由等效电路算出 iz(0)=12A=i(0) Uo 3Ω uc(0)=24V=uc(0+) 48V 10

10 三、初始值的计算 解： 换路前的“旧电路” 求图示电路在开关 闭合瞬间各支路电 流和电感电压。 1. 由换路前的“旧电路” 计算uC(0- )和iL (0- ) 。 iC(0- )=0，C视为开路。 uL (0- )=0，L视为短路。 iL (0- ) = 12A uC(0- ) = 24V = iL (0+ ) = uC(0+ ) R1 + - U0 S R2 iL iC C L + - uL + - uC R3 3W 2W 2W 48V i R1 + - U0 S R2 iL iC C L + - uL + - uC R3 3W 2W 2W 48V 由等效电路算出 i