安徽大学：《运筹学》课程习题详解（PPT讲稿）第三章 运输问题

运筹学教程 第三章习题解答 3.1与一般线性规划的数学模型相比，运输问题 的数学模型具有什么特征？ 答： 1、运输问题一定有有限最优解。 2、约束系数只取0或1。 3、约束系数矩阵的每列有两个1，而且只有两个 1。前m行中有一个1，或n行中有一个1。 4、对于产销平衡的运输问题，所有的约束都取 等式。 page 2 23 April 2025 School of Management

运筹学教程 School of Management page 2 23 April 2025 第三章习题解答 3.1 与一般线性规划的数学模型相比，运输问题 的数学模型具有什么特征? 答： 1、运输问题一定有有限最优解。 2、约束系数只取0或1。 3、约束系数矩阵的每列有两个1，而且只有两个 1。前m行中有一个1，或n行中有一个1。 4、对于产销平衡的运输问题，所有的约束都取 等式

运筹学教程 第三章习题解答 3.2运输问题的基可行解应满足什么条件？将其 填入运输表中时有什么体现？并说明在迭代计算过程 中对它的要求。 解：运输问题基可行解的要求是基变量的个数等 于m+n-1。填入表格时体现在数字格的个数也应该等 于m+n-1。在迭代过程中，要始终保持数字格的个数 不变。 page 3 23 April 2025 School of Management

运筹学教程 School of Management page 3 23 April 2025 3.2 运输问题的基可行解应满足什么条件？将其 填入运输表中时有什么体现？并说明在迭代计算过程 中对它的要求。 解：运输问题基可行解的要求是基变量的个数等 于m+n-1。填入表格时体现在数字格的个数也应该等 于m+n-1。在迭代过程中，要始终保持数字格的个数 不变。 第三章习题解答

运筹学教程 第三章习题解答 3.3试对给出运输问题初始基可行解的西北角法、 最小元素法和Vog©l法进行比较，分析给出的解之质量 不同的原因。 解：用西北角法可以快速得到初始解，但是由于 没有考虑运输价格，效果不好；最小元素法从最小的 运输价格入手，一开始效果很好，但是到了最后因选 择余地较少效果不好；V0g©l法从产地和销地运价的 级差来考虑问题，总体效果很好，但是方法较复杂。 page 4 23 April 2025 School of Management

运筹学教程 School of Management page 4 23 April 2025 3.3 试对给出运输问题初始基可行解的西北角法、 最小元素法和Vogel法进行比较，分析给出的解之质量 不同的原因。 解：用西北角法可以快速得到初始解，但是由于 没有考虑运输价格，效果不好；最小元素法从最小的 运输价格入手，一开始效果很好，但是到了最后因选 择余地较少效果不好；Vogel法从产地和销地运价的 级差来考虑问题，总体效果很好，但是方法较复杂。 第三章习题解答

运筹学教程 第三章习题解答 3.4详细说明用位势法（对偶变量法）求检验数的原 理。 解：原问题的检验数也可以利用对偶变量来计 算： C-(w,+y,)i=1,2,.m,j=1,2,.,n 其中，u和v就是原问题约束对应的对偶变量。由于 原问题的基变量的个数等于m+n-1。所以相应的检验 数就应该等于0。即有： cj-(4,+vj)=0i=1,2,.m,j=1,2,.,n page 5 23 April 2025 School of Management

运筹学教程 School of Management page 5 23 April 2025 3.4 详细说明用位势法(对偶变量法)求检验数的原 理。 解：原问题的检验数也可以利用对偶变量来计 算 ： 第三章习题解答  i j = ci j − (ui + vj ) i =1,2, m; j =1,2,  ,n 其中，ui和vj就是原问题约束对应的对偶变量。由于 原问题的基变量的个数等于m+n-1。所以相应的检验 数就应该等于0。即有： ci j − (ui + vj ) = 0 i =1,2, m; j =1,2,  ,n

运筹学教程 第三章习题解答 由于方程有m+n-1个，而变量有m+n个。所以上 面的方程有无穷多个解。任意确定一个变量的值都可 以通过方程求出一个解。然后再利用这个解就可以求 出非基变量的检验数了。 page 6 23 April 2025 School of Management

运筹学教程 School of Management page 6 23 April 2025 由于方程有m+n-1个，而变量有m+n个。所以上 面的方程有无穷多个解。任意确定一个变量的值都可 以通过方程求出一个解。然后再利用这个解就可以求 出非基变量的检验数了。 第三章习题解答

运筹学教程 第三章习题解答 3.5用表上作业法求解运输问题时，在什么情况 下会出现退化解？当出现退化解时应如何处理？ 解：当数字格的数量小于m+m-1时，相应的解就 是退化解。如果出现了退化解，首先找到同时划去的 行和列，然后在同时划去的行和列中的某个空格中填 入数字0。只要数字格的数量保持在m+n-1个的水平即 可。 page 7 23 April 2025 School of Management

运筹学教程 School of Management page 7 23 April 2025 3.5 用表上作业法求解运输问题时，在什么情况 下会出现退化解？当出现退化解时应如何处理？ 解：当数字格的数量小于m+n-1时，相应的解就 是退化解。如果出现了退化解，首先找到同时划去的 行和列，然后在同时划去的行和列中的某个空格中填 入数字0。只要数字格的数量保持在m+n-1个的水平即 可。 第三章习题解答

运筹学教程 第三章习题解答 3.6一般线性规划问题具备什么特征才能将其转 化为运输问题求解，请举例说明。 解：如果线性规划问题有“供”和“需”的关系， 并且有相应的“费用”，就可以考虑将线性规划问题 转成运输问题求解。例如，生产满足需求的问题。 page 8 23 April 2025 School of Management

运筹学教程 School of Management page 8 23 April 2025 3.6 一般线性规划问题具备什么特征才能将其转 化为运输问题求解，请举例说明。 解：如果线性规划问题有“供”和“需”的关系， 并且有相应的“费用”，就可以考虑将线性规划问题 转成运输问题求解。例如，生产满足需求的问题。 第三章习题解答

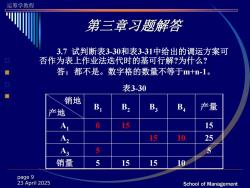
运筹学教程 第三章习题解答 3.7试判断表3-30和表3-31中给出的调运方案可 否作为表上作业法迭代时的基可行解？为什么？ 答：都不是。数字格的数量不等于m+n-1。 表3-30 销地 B B2 产量 产地 A 0 15 A2 15 10 25 A3 5 5 销量 5 15 15 10 page 9 23 April 2025 School of Management

运筹学教程 School of Management page 9 23 April 2025 3.7 试判断表3-30和表3-31中给出的调运方案可 否作为表上作业法迭代时的基可行解?为什么? 答：都不是。数字格的数量不等于m+n-1。 表3-30 销地 产地 B1 B2 B3 B4 产量 A1 0 15 15 A2 15 10 25 A3 5 5 销量 5 15 15 10 第三章习题解答

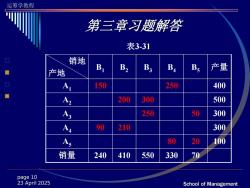
运筹学教程 第三章习题解答 表3-31 销地 产地 乃 B2B3B4B产量 Al 150 250 400 A2 200 300 500 250 50 300 A 90 210 300 A 80 20 100 销量 240 410 550 330 70 page 10 23 April 2025 School of Management

运筹学教程 School of Management page 10 23 April 2025 表3-31 销地 产地 B1 B2 B3 B4 B5 产量 A1 150 250 400 A2 200 300 500 A3 250 50 300 A4 90 210 300 A5 80 20 100 销量 240 410 550 330 70 第三章习题解答

运筹学教程 第三章习题解答 3.8表3-32和表333分别给出了各产地和各销地 的产量和销量，以及各产地至各销地的单位运价，试 用表上作业法求最优解。 表3-32 销地 产地 B2 B3 产量 Al 4 51 34 8 A2 61 2 5 2 8 A3 3 Z35 1 l 4 销量 6 5 6 3 20 page 11 23 April 2025 School of Management

运筹学教程 School of Management page 11 23 April 2025 3.8 表3-32和表3-33分别给出了各产地和各销地 的产量和销量，以及各产地至各销地的单位运价，试 用表上作业法求最优解。 表3-32 销地 产地 B1 B2 B3 B4 产量 A1 4 5 1 3 4 6 8 A2 6 1 2 5 2 0 8 A3 3 7 3 5 1 1 4 销量 6 5 6 3 20 第三章习题解答