《运筹学》课程教学资源（参考资料）8 多目标规划模型

8多目标规划模型 8.1引言 直到目前为止，我们都是假设只有一个目标。然而，事实上往往会有两个或两个以上的 目标。如果这些目标又是不相容的（就是说无法用一个目标取而带之），那么，我们的生活 就变得困难了或者说更加有趣了。生活中经常用“苹果和橙子不能兼得”来形容一个人处于 两难的境地。 下面给出一些不相容目标的例子： ◆投资的利润与风险， ◆一个公司的短期效益和长期效益， ◆一个政府机构的成本与服务， ◆一个行政机构的某个政策下不同人群的待遇（例如，农村人，城市人：机场附 近的居民，机场的旅客：渔民，水上运输公司，一个大湖附近的农民)。 我们可以将多目标情况分为两大类： 1)目标本质上不同（例如，风险与利润，成本与服务）】 a)可以确定权重： b)可以对目标的重要性进行排序。我们有所谓的优先目标。 2)目标本质上类似（就是说，从某种意义上看这些目标具有相等的权重）。 在公共建设工程中有很多多目标规划问题。一个特殊的例子就是中国长江的“三峡”水 利工程。我们注意以下几点：()工业用电大户的兴趣。他们希望平均水位高一点，以便可 以得到最大的发电量：(b)下游的农民的兴趣。他们希望平均水位低一点，以便可以蓄水防止 大的洪涝灾害：（©）航运部门的兴趣。他们希望水位可以适当的调节，以便保持平稳的水流， 使得大型船只也可以常年通行。()渔民和游客的兴趣。他们希望下泄的流量可以调节，以 便使得湖泊的水平面保持平稳：（©）环保人员的兴趣。他们一开始就不希望建设大坝。对于这 个独特三峡大坝，主张控制流量的人建议在雨季到来之前的蓄水的高度应该是海拔459英尺， 以便可以预防更大的洪涝灾害。然而，电力生产部门建议蓄水的高度应该是海拔574英尺

1 8 多目标规划模型 8.1 引言 直到目前为止，我们都是假设只有一个目标。然而，事实上往往会有两个或两个以上的 目标。如果这些目标又是不相容的（就是说无法用一个目标取而带之），那么，我们的生活 就变得困难了或者说更加有趣了。生活中经常用“苹果和橙子不能兼得”来形容一个人处于 两难的境地。 下面给出一些不相容目标的例子： ◆ 投资的利润与风险， ◆ 一个公司的短期效益和长期效益， ◆ 一个政府机构的成本与服务， ◆ 一个行政机构的某个政策下不同人群的待遇 (例如，农村人，城市人；机场附 近的居民，机场的旅客；渔民，水上运输公司，一个大湖附近的农民)。 我们可以将多目标情况分为两大类： 1）目标本质上不同(例如，风险与利润，成本与服务). a) 可以确定权重； b) 可以对目标的重要性进行排序。我们有所谓的优先目标。 2）目标本质上类似(就是说，从某种意义上看这些目标具有相等的权重)。 在公共建设工程中有很多多目标规划问题。一个特殊的例子就是中国长江的“三峡”水 利工程。 我们注意以下几点：(a) 工业用电大户的兴趣。他们希望平均水位高一点，以便可 以得到最大的发电量；(b)下游的农民的兴趣。他们希望平均水位低一点，以便可以蓄水防止 大的洪涝灾害；(c)航运部门的兴趣。他们希望水位可以适当的调节，以便保持平稳的水流， 使得大型船只也可以常年通行。(d) 渔民和游客的兴趣。他们希望下泄的流量可以调节，以 便使得湖泊的水平面保持平稳；(e)环保人员的兴趣。他们一开始就不希望建设大坝。对于这 个独特三峡大坝，主张控制流量的人建议在雨季到来之前的蓄水的高度应该是海拔 459 英尺， 以便可以预防更大的洪涝灾害。然而，电力生产部门建议蓄水的高度应该是海拔 574 英尺

以便生产出更多的电能。 ●多重最优解和多目标 如果你建立了模型，且具有多重最优解，那么，这很自然地就说明了存在多个目标。你 应该再仔细看看目标函数。用户是不喜欢多重最优解的。如果具有多重最优解，最普通的解 决办法就是从中随机地选择一个。如果人们的工作或工资就取决于你掷“硬币”的结果，这 总会令人感到不愉快。即使不是得失攸关，多重最优解也让人烦恼。如果人们在不同的计算 机上求解同样一个问题会得到不同解答（即便目标函数值相同），人们也一定会为此而感到 沮丧。 也许有些读者会认为将这些最优解平均一下，就可以得到最终唯一最好的解答。很不幸， 这常常是行不通的。这是因为： a)列举出所有多重最优解很困难： )平均解答未必具有吸引力，而且，如果涉及整数变量，平均解答可能都不是可行解。 8.2处理多标准问题的方法 处理多标准问题有很多方法。下面我们介绍一些更加实用的方法。 8.2.1帕累托最优解和多目标 如果多目标问题的一个解满足：所有其它的解不如该解，且至少有一个目标是严格不如， 那么，这个解就称为帕累托最优解。一个帕累托最优解不可以被任何其它解代替。很显然， 我们就是研究帕累托最优解。如果我们不仔细选择我们的目标，我们可能得到一些解，但是 得不到帕累托最优解。有一些计算多目标线性规划程序可以给出所有无法替代的解。对于一 个小问题，一个决策者可以凭借个人的目标从所有无法替代极的解中简单地选择出最具吸引 力的解。而对于一个大的问题，无法替代极的解的个数很容易超过100个，所以，利用这种 方法就很难找到最具吸引力的解。 8.2.2效用函数的方法 解决多目标问题的一个很有吸引力的方法就是定义一个效用函数。如果决策变量是

2 以便生产出更多的电能。 ⚫ 多重最优解和多目标 如果你建立了模型，且具有多重最优解，那么，这很自然地就说明了存在多个目标。 你 应该再仔细看看目标函数。用户是不喜欢多重最优解的。如果具有多重最优解，最普通的解 决办法就是从中随机地选择一个。如果人们的工作或工资就取决于你掷“硬币”的结果，这 总会令人感到不愉快。即使不是得失攸关，多重最优解也让人烦恼。如果人们在不同的计算 机上求解同样一个问题会得到不同解答（即便目标函数值相同），人们也一定会为此而感到 沮丧。 也许有些读者会认为将这些最优解平均一下，就可以得到最终唯一最好的解答。很不幸， 这常常是行不通的。这是因为： a) 列举出所有多重最优解很困难； b) 平均解答未必具有吸引力，而且，如果涉及整数变量，平均解答可能都不是可行解。 8.2 处理多标准问题的方法 处理多标准问题有很多方法。下面我们介绍一些更加实用的方法。 8.2.1 帕累托最优解和多目标 如果多目标问题的一个解满足：所有其它的解不如该解，且至少有一个目标是严格不如， 那么，这个解就称为帕累托最优解。一个帕累托最优解不可以被任何其它解代替。很显然， 我们就是研究帕累托最优解。如果我们不仔细选择我们的目标，我们可能得到一些解，但是 得不到帕累托最优解。有一些计算多目标线性规划程序可以给出所有无法替代的解。对于一 个小问题，一个决策者可以凭借个人的目标从所有无法替代极的解中简单地选择出最具吸引 力的解。而对于一个大的问题，无法替代极的解的个数很容易超过 100 个，所以，利用这种 方法就很难找到最具吸引力的解。 8.2.2 效用函数的方法 解决多目标问题的一个很有吸引力的方法就是定义一个效用函数。如果决策变量是 xl

3 X2.Xm我们可以“简单地”构造一个效用函数u(X,为.X),它表示对决策变量 的任何可能的取值X,:.，都有一个实数与之对应。这是研究最优化问题的一个很 有用的方法。当然，这种方法也有它的局限性：()构造这个函数可能要做很多工作：(b)这个 函数可能高度非线性。特性(b)意味着可能不能利用LP来求解问题。 8.2.3包络线 如果我们只有两个或三个目标，包络线不但是效用函数方法中最有吸引力的，也是非常 实用的。我们可以简单地构造一条曲线（就是所谓的“效用前沿线”），它表明我们是如何用 一个目标替换另一个目标的。使用包络线最有名的例子就是描述金融投资组合中两个目标之 间的关系。这两个目标是期望利润和风险。我们想得到利润高而风险低的资产组合。图8.1 表明了利润和风险之间的一般关系。曲线上的每一点都是帕累托最优解。就是说，对于曲 线上的任何一点，不存在其它的点，使得利润比它高而风险比它低。 可能一个决策者没有经历构造他的效用函数的烦恼，但是他也许可以看到这个包络线， 会说：“啊，我对拥有8%的期望利润和3%的标准差很满意”。 图8.1期望利润和风险的包络线 0 风险〔就是利润标准差〕 8.2.4实例：Ad Lib的经营策略 AdLb是一个广告代理商，他要为他的一个客户求解一个所谓的媒体选择问题。他打算 在下面5种媒体上做广告：深夜TV(TVL),黄金时间TV(TVP),广告栏(BLB),报纸NEW)

3 x2 . xn, 我们可以“简单地”构造一个效用函数 u (xl, x2 . xn)，它表示对决策变量 的任何可能的取值 xl, x2 . xn ，都有一个实数与之对应。这是研究最优化问题的一个很 有用的方法。当然，这种方法也有它的局限性：(a)构造这个函数可能要做很多工作；(b)这个 函数可能高度非线性。特性(b)意味着可能不能利用 LP 来求解问题。 8.2.3 包络线 如果我们只有两个或三个目标，包络线不但是效用函数方法中最有吸引力的，也是非常 实用的。我们可以简单地构造一条曲线（就是所谓的“效用前沿线”），它表明我们是如何用 一个目标替换另一个目标的。使用包络线最有名的例子就是描述金融投资组合中两个目标之 间的关系。这两个目标是期望利润和风险。我们想得到利润高而风险低的资产组合。图 8.1 表明了利润和风险之间的一般关系。曲线上的每一点都是帕累托最优解。 就是说，对于曲 线上的任何一点，不存在其它的点，使得利润比它高而风险比它低。 可能一个决策者没有经历构造他的效用函数的烦恼，但是他也许可以看到这个包络线， 会说：“啊，我对拥有 8%的期望利润和 3%的标准差很满意”。 图 8.1 期望利润和风险的包络线 8.2.4 实例: Ad Lib 的经营策略 Ad Lib 是一个广告代理商，他要为他的一个客户求解一个所谓的媒体选择问题。他打算 在下面 5 种媒体上做广告：深夜 TV (TVL)，黄金时间 TV (TVP)，广告栏(BLB)，报纸(NEW)

和广播(RAD)。这些广告打算覆盖七类不同的人群市场。 下面的表格给出了1美元的广告费用在每个媒体下每类人群中可以暴光的人数。倒数第 2行的数字是七类人群最低的暴光人数（无论多少费用都要达到这个数字），最后一行数字是 七类人群饱和的暴光人数。就是说，超过这个数字以外的暴光没有任何效果。暴光人数在这 两个数字之间才是有效的暴光。 Ad Lib经营策略的暴光统计 暴光人数(1000's/$1000) 人群市场 3 4 5 7 TVL 10 450 5 TVP 10 30 5 12 BLB 20 5 NEW 8 6 10 RAD 6 5 10 11 最低暴光人数(1,000's) 25 40 60 120 40 11 15 饱和暴光人数(1,000's) 60 70 120 140 80 2555 每一种媒体上的广告费用应该花多少呢？这里有两个目标()成本（我们希望它少一 点)，(b)有效的暴光人数（我们希望多一点）。一开始，我们规定广告费用不能超过$11,000。 定义： 决策变量 TVL,TVP,等=在TVL,TVP,等广告上的花费（每1,000's): UXL,X2,等=市场L,2,.7上的超额有效暴光人数（就是等于min{饱和暴光 人数，实际暴光人数}一最低暴光人数)： COST =广告总成本： USEFULX =总的超额有效暴光人数。 我们可以将约束可以分成两大类。一类是： 一个人群市场的暴光人数>=最低的暴光人数+有效的超额暴光人数。 另一个是： 一个人群市场的有效超额暴光人数<=饱和暴光人数一最低的暴光人数。 这样，我们就可以得到下面的模型： MODEL:

4 和广播 (RAD)。这些广告打算覆盖七类不同的人群市场。 下面的表格给出了 1 美元的广告费用在每个媒体下每类人群中可以暴光的人数。倒数第 2 行的数字是七类人群最低的暴光人数（无论多少费用都要达到这个数字），最后一行数字是 七类人群饱和的暴光人数。就是说，超过这个数字以外的暴光没有任何效果。暴光人数在这 两个数字之间才是有效的暴光。 Ad Lib 经营策略的暴光统计 暴光人数（1000's/$1000） 人 群 市 场 1 2 3 4 5 6 7 TVL 10 4 50 5 2 TVP 10 30 5 12 BLB 20 5 3 NEW 8 6 10 RAD 6 5 10 11 4 最低暴光人数（1,000's） 25 40 60 120 40 11 15 饱和暴光人数（1,000's） 60 70 120 140 80 25 55 每一种媒体上的广告费用应该花多少呢？这里有两个目标 (a) 成本(我们希望它少一 点)，(b)有效的暴光人数(我们希望多一点)。一开始，我们规定广告费用不能超过$11,000。 定义： 决策变量: TVL, TVP, 等 = 在 TVL， TVP，等广告上的花费（每 1,000's）； UX1, UX2, 等 = 市场 1, 2, .7 上的超额有效暴光人数 (就是等于 min {饱和暴光 人数，实际暴光人数} – 最低暴光人数)； COST = 广告总成本； USEFULX = 总的超额有效暴光人数。 我们可以将约束可以分成两大类。一类是： 一个人群市场的暴光人数 >= 最低的暴光人数 + 有效的超额暴光人数。 另一个是： 一个人群市场的有效超额暴光人数 <= 饱和暴光人数 – 最低的暴光人数。 这样，我们就可以得到下面的模型: MODEL:

5 [UEXP]MAX-USEFULX;!Maximize有效的超额暴光人数： [LIMC0ST]C0ST=0;！暴光需求： [DEFCOST]TVL TVP BLB NEW RAD COST; [DEFEXP]UX1 UX2 UX3 UX4 UX5 UX6 UX7 USEFULX; (MKT1] 20*BLB 8 NEW -0X1>=25: [MKT2]10 TVL +10 TVP +6*RAD -0X2>=40: [MKT31 4 TVL +30 *TVP +5*RAD -0X3>=60: [MKT4]50 TVL +5*TVP +10*RAD -0X4>=120: [MKT5]5 TVL 12 TVP 11*RAD -0X5>=40: [MKT6] 5*BLB+6 NEW+4 *RAD -0X6>=11; [MKT7]2 *TVL +3*BLB +10*NEW -UX7>=15: [RANGE1] UX1<=35; [RANGE2] UX2<=30: [RANGE3] UX3<=60: [RANGE4] UX4<=20: [RANGE5] UX5<=40: [RANGE6] 0X6<=14; [RANGE7] 0X7<=40: END 下面是这个模型的部分解答： Global optimal solution found at step: 16 Objective value: 196.7626 Variable Value Reduced Cost USEFULX 196.7626 0.0000000 COST 11.00000 0.0000000 TVL 1.997602 0.0000000 TVP 3.707434 0.0000000 BLB 2.908873 0.0000000 NEW 0.2278177 0.0000000 RAD 2.158273 0.0000000

5 [UEXP] MAX = USEFULX ; ! Maximize 有效的超额暴光人数; [LIMCOST] COST = 0;! 暴光需求; [DEFCOST] TVL + TVP + BLB + NEW + RAD = COST; [DEFEXP] UX1 + UX2 + UX3 + UX4 + UX5 + UX6 + UX7 = USEFULX; [MKT1] 20 * BLB + 8 * NEW - UX1 >= 25; [MKT2] 10 * TVL + 10 * TVP + 6 * RAD - UX2 >= 40; [MKT3] 4 * TVL + 30 * TVP + 5 * RAD - UX3 >= 60; [MKT4] 50 * TVL + 5 * TVP + 10 * RAD - UX4 >= 120; [MKT5] 5 * TVL + 12 * TVP + 11 * RAD - UX5 >= 40; [MKT6] 5 * BLB + 6 * NEW + 4 * RAD - UX6 >= 11; [MKT7] 2 * TVL + 3 * BLB + 10 * NEW - UX7 >= 15; [RANGE1] UX1 <= 35; [RANGE2] UX2 <= 30; [RANGE3] UX3 <= 60; [RANGE4] UX4 <= 20; [RANGE5] UX5 <= 40; [RANGE6] UX6 <= 14; [RANGE7] UX7 <= 40; END 下面是这个模型的部分解答： Global optimal solution found at step: 16 Objective value: 196.7626 Variable Value Reduced Cost USEFULX 196.7626 0.0000000 COST 11.00000 0.0000000 TVL 1.997602 0.0000000 TVP 3.707434 0.0000000 BLB 2.908873 0.0000000 NEW 0.2278177 0.0000000 RAD 2.158273 0.0000000

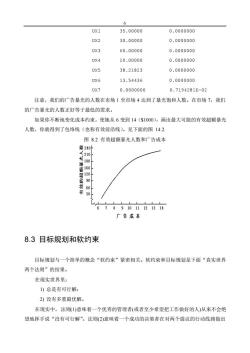
6 0X1 35.00000 0.0000000 UX2 30.00000 0.0000000 UX3 60.00000 0.0000000 0X4 20.00000 0.0000000 0X5 38.21823 0.0000000 UX6 13.54436 0.0000000 UX7 0.0000000 0.7194281E-02 注意，我们的广告暴光的人数在市场1至市场4达到了暴光饱和人数。在市场7，我们 的广告暴光的人数正好等于最低的需求。 如果你不断地变化成本约束，使她从6变到14($1000)，画出最大可能的有效超额暴光 人数，你就得到了包络线（也称有效前沿线）。见下面的图14.2. 图8.2有效超额暴光人数和广告成本 亲240 210 180 60 67891011121314 广告成本 8.3目标规划和软约束 目标规划与一个简单的概念“软约束”紧密相关。软约束和目标规划是下面“真实世界 两个法则”的结果。 在现实世界里： 1)总是有可行解： 2)没有多重最优解。 在现实中，法则(1)意味着一个优秀的管理者（或者至少希望把工作做好的人）从来不会绝 望地挥手说“没有可行解”。法则(2)意味着一个成功的决策者在对两个提议的行动线路做出

6 UX1 35.00000 0.0000000 UX2 30.00000 0.0000000 UX3 60.00000 0.0000000 UX4 20.00000 0.0000000 UX5 38.21823 0.0000000 UX6 13.54436 0.0000000 UX7 0.0000000 0.7194281E-02 注意，我们的广告暴光的人数在市场 1 至市场 4 达到了暴光饱和人数。在市场 7，我们 的广告暴光的人数正好等于最低的需求。 如果你不断地变化成本约束，使她从 6 变到 14（$1000），画出最大可能的有效超额暴光 人数，你就得到了包络线（也称有效前沿线）。见下面的图 14.2. 图 8.2 有效超额暴光人数和广告成本 8.3 目标规划和软约束 目标规划与一个简单的概念“软约束”紧密相关。软约束和目标规划是下面“真实世界 两个法则”的结果。 在现实世界里： 1) 总是有可行解； 2) 没有多重最优解。 在现实中，法则(1)意味着一个优秀的管理者(或者至少希望把工作做好的人)从来不会绝 望地挥手说“没有可行解”。法则(2)意味着一个成功的决策者在对两个提议的行动线路做出

选择时，总是有足够的标准区分出最好的行动线路。 通过前面的模型可知，这两个法则意味着一个好的模型应该：()总是有可行解：(b)没有 多重最优解。 8.3.1实例：多重最优解的第2个选择目标 下面介绍这个目标。我们使用的问题与第7章讨论的职员问题(7天/周)类似。变量： MT,W,RE,S,N分别表示在星期一、二、三、四、五、六、日每天开始雇佣的人数（每人 连续工作5天)。 MODEL: MIN=9*M+9*T+9*W+9*R+9*E+9*S+9*N; [MON] M +R+F+S+N >= 3: (TUE] M+T +F+S+N >= 3; [WED] M+T+W +S+N >= 8; [THU] M+T+W+R +N >= 8: (FRI] M+T+W+R+F >= 8: [SAT] T+W+R+F+S >= 3: [SUN] W+R+F+S+N >= 3; END 求解模型后可以得到下面的解答：， Global optimal solution found at step: 8 Obiective value: 72.00000 Variable Value Reduced Cost g 3.000000 0.000000 2.000000 0.000000 3.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 9.000000

7 选择时，总是有足够的标准区分出最好的行动线路。 通过前面的模型可知，这两个法则意味着一个好的模型应该：(a)总是有可行解；(b)没有 多重最优解。 8.3.1 实例：多重最优解的第 2 个选择目标 下面介绍这个目标。我们使用的问题与第 7 章讨论的职员问题（7 天/周）类似。变量： M, T, W, R, F, S, N 分别表示在星期一、二、三、四、五、六、日每天开始雇佣的人数（每人 连续工作 5 天）。 MODEL: MIN = 9*M + 9*T + 9*W + 9*R + 9*F + 9*S + 9*N; [MON] M + R + F + S + N >= 3; [TUE] M + T + F + S + N >= 3; [WED] M + T + W + S + N >= 8; [THU] M + T + W + R + N >= 8; [FRI] M + T + W + R + F >= 8; [SAT] T + W + R + F + S >= 3; [SUN] W + R + F + S + N >= 3; END 求解模型后可以得到下面的解答：. Global optimal solution found at step: 8 Objective value: 72.00000 Variable Value Reduced Cost M 3.000000 0.000000 T 2.000000 0.000000 W 3.000000 0.000000 R 0.000000 0.000000 F 0.000000 0.000000 S 0.000000 9.000000

8 N 0.000000 9.000000 RoW slack or Surplus Dual Price 1 72.00000 1.000000 MON 0.000000 0.000000 TUE 2.000000 0.000000 WED 0.000000 0.000000 THU 0.000000 0.000000 FRI 0.000000 -9.00000 SAT 2.000000 0.000000 SUN 0.000000 0.000000 注意，这个问题有多重最优解（例如，“WED”行的递减成本和对偶价格都是O)。这个解 答在星期六和星期天都有剩余的劳动力(2人)，其他时间无剩余劳动力。这里，不同的最优 解就表现在剩余劳动力的分配上不相同。这个解答在星期六和星期天有太多的剩余劳动力， 而在其他时间却没有剩余劳动力。 研究以下这个问题的多目标，我们认为： a)我们最重要的目标就是职员的总成本最小： b)次要的日标是剩余的劳动力分配要尽量要少而合理。在不影响第1个标准的前提下， 每天的剩余劳动力最好不要超过1个。 为了使得剩余劳动力的分配更加合理，我们增加了一些“剩余”变量XM、XT、等， 这些变量的值限制在0到1之间，并且赋予-1的价格（权重）。修改后的模型如下： MODEL: MIN =9*(M+R F+S+N+T+W) -(XM XT XW XR XF XS XN); [MON]M +R+F+S+N-XM>=3: [TUE]M +T +F+S+N-XT>=3: [WED]M T W +S+N-Xm>=8; [THU]M+T W+R +N-XR>=8; [FRI]M +T W+R F -XF>=8; [SAT] T+W+R+F+S -XS>=3; [SUN] W R F S N XN >=3; ！剩余人数限制：

8 N 0.000000 9.000000 Row Slack or Surplus Dual Price 1 72.00000 1.000000 MON 0.000000 0.000000 TUE 2.000000 0.000000 WED 0.000000 0.000000 THU 0.000000 0.000000 FRI 0.000000 -9.00000 SAT 2.000000 0.000000 SUN 0.000000 0.000000 注意，这个问题有多重最优解(例如，“WED”行的递减成本和对偶价格都是 0)。这个解 答在星期六和星期天都有剩余的劳动力（2 人），其他时间无剩余劳动力。这里，不同的最优 解就表现在剩余劳动力的分配上不相同。这个解答在星期六和星期天有太多的剩余劳动力， 而在其他时间却没有剩余劳动力。 研究以下这个问题的多目标，我们认为： a) 我们最重要的目标就是职员的总成本最小； b) 次要的目标是剩余的劳动力分配要尽量要少而合理。在不影响第 1 个标准的前提下， 每天的剩余劳动力最好不要超过 1 个。 为了使得剩余劳动力的分配更加合理，我们增加了一些“剩余”变量 XM、XT、.等， 这些变量的值限制在 0 到 1 之间，并且赋予-1 的价格（权重）。修改后的模型如下： MODEL: MIN = 9*(M + R + F + S + N + T + W) -（XM + XT + XW + XR + XF + XS + XN）; [MON] M + R + F + S + N - XM >= 3; [TUE] M + T + F + S + N - XT >= 3; [WED] M + T + W + S + N - XW >= 8; [THU] M + T + W + R + N - XR >= 8; [FRI] M + T + W + R + F - XF >= 8; [SAT] T + W + R + F + S - XS >= 3; [SUN] W + R + F + S + N - XN >= 3; ! 剩余人数限制;

9 「EXM1 M<=1: [EXT] XT<=1: [EXW] XW<=1: [EXR] XR<=1 [EXF] XF<=1: [EXS] XS<=1; [EXN] XN<=1: END 解答是： Global optimal solution found at step: 20 Objective value: 68.00000 Variable Value Reduced Cost M 4.000000 0.0000000 0.000000 0.0000000 0.000000 0.0000000 S 0.000000 4.000000 N 0.000000 4.000000 0.000000 0.0000000 4.000000 0.0000000 XM 1.000000 0.0000000 XT 1.000000 0.0000000 XW 0.000000 0.0000000 XR 0.000000 0.0000000 XE 0.000000 4.000000 XS 1.000000 0.0000000 XN 1.000000 0.0000000 注意，虽然我们还是雇佣8个职员，但是，现在有4天剩余1人，职员分配更加合理。 这是一个更有吸引力的解答

9 [EXM] XM <= 1; [EXT] XT <= 1; [EXW] XW <= 1; [EXR] XR <= 1; [EXF] XF <= 1; [EXS] XS <= 1; [EXN] XN <= 1; END 解答是: Global optimal solution found at step: 20 Objective value: 68.00000 Variable Value Reduced Cost M 4.000000 0.0000000 R 0.000000 0.0000000 F 0.000000 0.0000000 S 0.000000 4.000000 N 0.000000 4.000000 T 0.000000 0.0000000 W 4.000000 0.0000000 XM 1.000000 0.0000000 XT 1.000000 0.0000000 XW 0.000000 0.0000000 XR 0.000000 0.0000000 XF 0.000000 4.000000 XS 1.000000 0.0000000 XN 1.000000 0.0000000 注意，虽然我们还是雇佣 8 个职员，但是，现在有 4 天剩余 1 人，职员分配更加合理。 这是一个更有吸引力的解答

10 8.3.2具有优先级别的目标规划 在上面介绍的方法中，我们需要对两个目标（成本和服务）选择适合的权重。在某些情 况下，一个目标显然要比另一个目标重要。虽然人们可以用权重来实现这种区别（例如，给 第1个目标赋99999999的权重，给第2个目标赋0.0000001的权重)，但是，我们有很多理 由认为最好还是不用这种方法。首先，有一个数字上的问题，特别是当目标个数超过两个 的时候，这个问题就越发明显。一个台计算机也无法在数据相差15个数量级的情况下进行 准确的计算（例如，100,000,000and.0000001)。 更为重要的是，我们可以将这种情况直接简单地说成：“第1个目标的重要性远远超过 其余的目标：第2个目标的重要性远远超过剩下的目标，.”等等。这种处理问题的方法有 时候称为具有优先级别的目标规划。下面我们用前面的职员问题来说明如何使用这种方法。 我们首先建立第一个模型。将最重要的目标COST的权重赋值1，将第2个目标EXTRA(有 效剩余)的权重赋值0（无权重）。 Model: !具有优先级别的目标规划 MIN =1 COST -0 EXTRA: [MON]M +R+F+S+N-XM>=3: [TUE]M +T +F+S+N-XT>=3: [WED]M+T W +S+N-Xm>=8; [THU]M T +W+R +N-XR>=8; [FRI]M T +W+R F -XE>=8: [SAT] T+W+R+F+S -XS>=3; [SUN] W +R F S N XN >3; !剩余人数限制： [EXM] XM<=1: [EXT] XT<=1: [EXW] XW<=1: [EXR] XR<=1: [EXF] XF<=1; [EXS] XS<=1; [EXN] XN<=1;

10 8.3.2 具有优先级别的目标规划 在上面介绍的方法中，我们需要对两个目标（成本和服务）选择适合的权重。在某些情 况下，一个目标显然要比另一个目标重要。虽然人们可以用权重来实现这种区别（例如，给 第 1 个目标赋 99999999 的权重，给第 2 个目标赋 0.0000001 的权重），但是，我们有很多理 由认为最好还是不用这种方法。 首先，有一个数字上的问题，特别是当目标个数超过两个 的时候，这个问题就越发明显。一个台计算机也无法在数据相差 15 个数量级的情况下进行 准确的计算(例如，100,000,000 and .000000l)。 更为重要的是，我们可以将这种情况直接简单地说成：“第 1 个目标的重要性远远超过 其余的目标；第 2 个目标的重要性远远超过剩下的目标，.”等等。这种处理问题的方法有 时候称为具有优先级别的目标规划。 下面我们用前面的职员问题来说明如何使用这种方法。 我们首先建立第一个模型。将最重要的目标 COST 的权重赋值 1，将第 2 个目标 EXTRA（有 效剩余）的权重赋值 0（无权重）。 Model： ! 具有优先级别的目标规划 MIN = 1 * COST - 0 * EXTRA; [MON] M + R + F + S + N - XM >= 3; [TUE] M + T + F + S + N - XT >= 3; [WED] M + T + W + S + N - XW >= 8; [THU] M + T + W + R + N - XR >= 8; [FRI] M + T + W + R + F - XF >= 8; [SAT] T + W + R + F + S - XS >= 3; [SUN] W + R + F + S + N - XN >= 3; ! 剩余人数限制; [EXM] XM <= 1; [EXT] XT <= 1; [EXW] XW <= 1; [EXR] XR <= 1; [EXF] XF <= 1; [EXS] XS <= 1; [EXN] XN <= 1;