《运筹学》课程教学资源（参考资料）6 整数规划模型

6整数规划模型 6.1引言 在许多最优化的应用问题中，人们要限制决策变量必须取整数值。例如，GM公司雪佛 莱汽车的年生产量是相关模型的决策变量，如果解答中该决策变量的值是1,524,328.37辆， 那么，这个值人们是无法接受的。人们并不介意雪佛莱汽车年产量是1,524,328辆还是 1,524,329辆。当然，如果另一项研究的最优解是建议制造1.37架飞机，那时，世界上就会 有很多人对这个数字及其周边的数字感兴趣。很显然，如果人们限制决策变量取整数值，很 多最优化模型的价值和有效性都将得到改变。 所有商用最优化模型系统都具有让用户限制一定的决策变量为整数变量的能力。如何实 现用户的整数要求，不同的程序有着不同的处理方法。例如，在LINGO中，如果要限制变 量X取整数，只要在模型中增加语句@GN(X就可以了。 按照变量的类型可以对整数规划模型进行如下分类： 纯整数模型s.混合模型。在一个纯整数模型里，所有的变量都取整数。在一个混合模 型里，有一些变量限制取整数，而另一些变量可以连续取值。 01模型s.一般整数模型。在许多应用问题中，很多变量只能取0和1两个整数。所以， 在一些整数规划模型中要限制若干个变量只能取0或1两个 数值。 限制变量取整数的要求可能比读者最初的想象要大得多。表示开/关的01整数变量在模 型中经常出现。或许现实中的整数规划多半都是具有01变量的整数规划。 6.2开拓整数规划(IP)的能力 人们在使用LP的时候常常会遇到一些用线性规划无法解决的困难。接下来，我们将介 绍如何利用整数变量来解决这些困难的方法。当然，一旦引入了整数变量，相应的模型就

6 整数规划模型 6.1 引言 在许多最优化的应用问题中，人们要限制决策变量必须取整数值。例如，GM 公司雪佛 莱汽车的年生产量是相关模型的决策变量，如果解答中该决策变量的值是 1,524,328.37 辆， 那么，这个值人们是无法接受的。人们并不介意雪佛莱汽车年产量是 1,524,328 辆还是 1,524,329 辆。当然，如果另一项研究的最优解是建议制造 1.37 架飞机，那时，世界上就会 有很多人对这个数字及其周边的数字感兴趣。很显然，如果人们限制决策变量取整数值，很 多最优化模型的价值和有效性都将得到改变。 所有商用最优化模型系统都具有让用户限制一定的决策变量为整数变量的能力。如何实 现用户的整数要求，不同的程序有着不同的处理方法。例如，在 LINGO 中，如果要限制变 量 X 取整数，只要在模型中增加语句@GIN(X)就可以了。 按照变量的类型可以对整数规划模型进行如下分类： 纯整数模型 vs.混合模型。 在一个纯整数模型里，所有的变量都取整数。在一个混合模 型里，有一些变量限制取整数，而另一些变量可以连续取值。 0/1 模型 vs.一般整数模型。在许多应用问题中，很多变量只能取 0 和 1 两个整数。所以， 在一些整数规划模型中要限制若干个变量只能取 0 或 1 两个 数值。 限制变量取整数的要求可能比读者最初的想象要大得多。表示开/关的 0/1 整数变量在模 型中经常出现。或许现实中的整数规划多半都是具有 0/1 变量的整数规划。 6.2 开拓整数规划（IP）的能力 人们在使用 LP 的时候常常会遇到一些用线性规划无法解决的困难。接下来，我们将介 绍如何利用整数变量来解决这些困难的方法。当然 ，一旦引入了整数变量，相应的模型就

变成了P模型。多数困难只要用0/1变量就可以解决而无需用一般的整数变量。0/1二元变 量可以表示范围非常广泛的诸如“去或是不去”、“生产或是购买”之类的决策问题。有时称 0/1二元变量为“哈姆雷特”变量。为了纪念逻辑学家George Boole,有时称0/1二元变量 为布尔变量。George Boole发明了变量只取两个数值“真”或“假”的布尔代数。当然，用 数值1表示“真”，用数值0表示“假”在概念上也是一个飞跃。 6.2.1用0/1二元变量表示一般的整数变量 有一些运算法则在应用时限制只能利用01整数变量。从概念上来看，任何在一定范围 内取值的整数变量都可以用一些01变量来表示。例如，假设限制X的取值集合是 [0,1,2,.,15。如果引入4个0/1变量：y,2,y3和y4,则变量X的任何一个值都可以用1+ 2×y+4×y3+8×y4代替。注意，[0,1,2，.，15)中的任何一个值都可以用一组y1,y2,y3和y4的值 表示。如果变量X的最大值可以取到31，你就需要5个0/1变量。如果最大值达到63，你 就需要6个01变量。事实上，如果你用k个01变量，那么，你可以表示的最大值就是2-1。 你可以记：VMAX=2k1。通过对这个等式取对数你就会发现，如果用0/1变量表示一般的 整数变量，所需01变量的个数近似为以2为底变量X最大取值的对数。 尽管这种替换是正确的，但还是要尽量避免。这是因为大多数整数规划模型在进行了这 种替换后的效率都不是很高。 6.2.2批量规模最小化约束 如果对经济活动的规模不加任何限制，效果并不是很好。因此，许多决策者对活动要指 定一个最小批量规模。例如，一个规模较大的中介公司要求买进和卖出的业务量至少要达到 100。用一个0/1变量就可以处理这个约束。令： x=活动的实际水平（例如，购买的股票数量）， y=1,只有当x>0时成立。Y是0/1变量， B=变量x的最小值（例如，100）， U=变量x已知的上限值。 下面两个约束将迫使最小批量规模条件成立： x≤Uy By≤X

变成了 IP 模型。多数困难只要用 0/1 变量就可以解决而无需用一般的整数变量。0/1 二元变 量可以表示范围非常广泛的诸如“去或是不去”、“生产或是购买”之类的决策问题。有时称 0/1 二元变量为“哈姆雷特”变量。为了纪念逻辑学家 George Boole ，有时称 0/1 二元变量 为布尔变量 。George Boole 发明了变量只取两个数值“真”或“假”的布尔代数。当然，用 数值 1 表示“真”，用数值 0 表示“假”在概念上也是一个飞跃。 6.2.1 用 0/1 二元变量表示一般的整数变量 有一些运算法则在应用时限制只能利用 0/1 整数变量。从概念上来看，任何在一定范围 内取值的整数变量都可以用一些 0/1 变量来表示。例如，假设限制 X 的取值集合是 [0,1,2,.,15]。 如果引入 4 个 0/1 变量：y1, y2, y3 和 y4，则变量 X 的任何一个值都可以用 y1 + 2×y2 + 4×y3 + 8×y4 代替。注意，[0,1,2,.,15]中的任何一个值都可以用一组 y1, y2, y3 和 y4 的值 表示。如果变量 X 的最大值可以取到 31，你就需要 5 个 0/1 变量。如果最大值达到 63，你 就需要 6 个 0/1 变量。事实上，如果你用 k 个 0/1 变量，那么，你可以表示的最大值就是 2 k -1。 你可以记：VMAX = 2k -1。通过对这个等式取对数你就会发现，如果用 0/1 变量表示一般的 整数变量，所需 0/1 变量的个数近似为以 2 为底变量 X 最大取值的对数。 尽管这种替换是正确的，但还是要尽量避免。这是因为大多数整数规划模型在进行了这 种替换后的效率都不是很高。 6.2.2 批量规模最小化约束 如果对经济活动的规模不加任何限制，效果并不是很好。因此，许多决策者对活动要指 定一个最小批量规模。例如，一个规模较大的中介公司要求买进和卖出的业务量至少要达到 100。用一个 0/1 变量就可以处理这个约束。令： x =活动的实际水平(例如，购买的股票数量)， y = 1, 只有当 x >0 时成立。Y 是 0/1 变量， B = 变量 x 的最小值 (例如，100)， U= 变量 x 已知的上限值。 下面两个约束将迫使最小批量规模条件成立： x ≤ Uy By ≤ x

如果y=0,那么第1个约束将迫使变量x=0。而如果y=1,第2个约束将迫使变量x 不少于B。所以，y实际上就是一个开关变量，它迫使变量x要么取值O,要么取值大于B。 选择常数U要特别注意，为了提高计算效率，在保证合理性的前提下，常数U的选择应该尽 量地小。 6.2.3固定收费问题 与最小批量规模情况很相似的一个问题就是一个活动的成本函数是固定成本加上呈线 性变化的可变成本。详见图6-1。 Cost 图6-1固定成本加上线性变化的可变成本的成本曲线 定义x,y和U如前，令K表示当x>O时的固定成本。那么，下面的语句将会出现在目 标函数中： Minimize Ky +cx+. subject to x≤Uy 目标函数中的项目Ky暗示：除非成本K发生，否则x的值不能大于0。同样，为了提 高计算的效率，常数U应该尽量小。 6.2.4简单的工厂定位问题(SPL) 求解简单的工厂定位问题($PL)就会遇到固定收费问题。下面给出详细说明：

如果 y = 0，那么第 1 个约束将迫使变量 x = 0。而如果 y = 1，第 2 个约束将迫使变量 x 不少于 B。所以，y 实际上就是一个开关变量，它迫使变量 x 要么取值 0，要么取值大于 B。 选择常数 U 要特别注意，为了提高计算效率，在保证合理性的前提下，常数 U 的选择应该尽 量地小。 6.2.3 固定收费问题 与最小批量规模情况很相似的一个问题就是一个活动的成本函数是固定成本加上呈线 性变化的可变成本。详见图 6-1。 图 6-1 固定成本加上线性变化的可变成本的成本曲线 定义 x, y 和 U 如前，令 K 表示当 x > 0 时的固定成本。那么，下面的语句将会出现在目 标函数中： Minimize Ky + cx +. subject to x ≤ Uy . . . 目标函数中的项目 Ky 暗示：除非成本 K 发生，否则 x 的值不能大于 0。同样，为了提 高计算的效率，常数 U 应该尽量小。 6.2.4 简单的工厂定位问题(SPL) 求解简单的工厂定位问题(SPL)就会遇到固定收费问题。下面给出详细说明：

n=工厂打算定位（或开工）的工地数目， =消费者（或需求点）的数目，每一个消费者必须指定一个工厂， k=可以开工的工厂数目， f=一个工厂在工地i开工的固定成本（例如，每年），i=1,2,.,n, c=在工地i开工的工厂被指派给消费者j的成本（例如，每年），i=L,2,.,n和j=L, 2,.,m。 这个问题的目标就是确定工厂将要定位或开工的工地集合，以便为每一个消费者提供服 务。 定义决策变量： y:=1如果一个工厂被定位在工地i,否则0， x=1如果消费者j被指定到工地i的工厂，否则0。 这个问题是一个很简单的P模型： Minimize ∑fy+∑∑cx (1) subject to ∑x=1 j=1,2,.,m (2) ∑，≤my i=1,2, (3) ∑y=k (4) yi=0or1 i=1,2,.,n (5) x=0or1i=1,2,.,n,j=1,2,.,m (6) 约束(2)将迫使消费者j被指定到一个确定的工地。如果一个消费者被指定到工地，约 束(3)将迫使有一个工厂定位到工地i。 我们再次提醒读者：尽管这种结构的模型并不是很大，但求解时仍需要非常多的计算时 间。产生困难的原因是这个问题属于整数规划。如果我们去掉约束(5)和(6)，然后再去求解（相 当于一个LP),得到的是分数解答，与最优整数规划解答相差甚远。 用下面的语句代替(3)： x≤y1i=1,2,.,nj=1,2,.,m(3) 如果有20个可能的工地和60个消费者，集合(3)有20个约束，而集合(3)有20×60=1,200

n = 工厂打算定位（或开工）的工地数目， m = 消费者（或需求点）的数目，每一个消费者必须指定一个工厂， k = 可以开工的工厂数目， fi = 一个工厂在工地 i 开工的固定成本(例如，每年) ，i = 1,2,.,n， cij = 在工地 i 开工的工厂被指派给消费者 j 的成本(例如，每年) ，i = 1,2,.,n 和 j = l, 2,.,m。 这个问题的目标就是确定工厂将要定位或开工的工地集合，以便为每一个消费者提供服 务。 定义决策变量： yi = 1 如果一个工厂被定位在工地 i, 否则 0, xij = 1 如果消费者 j 被指定到工地 i 的工厂，否则 0。 这个问题是一个很简单的 IP 模型: Minimize = =  = + n i n i m j i i ij ij f y c x 1 1 1 (1) subject to = = n i ij x 1 1 j = 1,2,.,m (2)  =  m j ij myi x 1 i = 1,2,.,n (3) = = n i i y k 1 (4) yi = 0 or 1 i = 1,2,.,n (5) xij= 0 or l i = 1,2,.,n, j = 1,2,.,m (6) 约束(2)将迫使消费者 j 被指定到一个确定的工地。如果一个消费者被指定到工地 i，约 束(3)将迫使有一个工厂定位到工地 i。 我们再次提醒读者：尽管这种结构的模型并不是很大，但求解时仍需要非常多的计算时 间。产生困难的原因是这个问题属于整数规划。如果我们去掉约束(5)和(6)，然后再去求解（相 当于一个 LP），得到的是分数解答，与最优整数规划解答相差甚远。 用下面的语句代替 (3)： xij ≤ yi i = 1,2,.,n j = 1,2,.,m (3') 如果有20个可能的工地和60个消费者，集合(3)有20个约束，而集合(3')有20 × 60 = 1,200

个约束。然而，从经验上看，当用(3)代替(3)而将这个问题化成一个LP来求解时，解答自然 是整数。 6.2.5能力受限制的工厂定位问题(CPL) 如果一个工厂把满足需求的数量作为重点考虑的因素，那么从SPL问题就会引出CPL 问题。特别地，CL问题假设每一个消费者的需求数量己知，每一个工厂生产的产品数量 受产品总量的限制。额外的参数定义如下： D=消费者j的需求量， K=定位于工地i工厂的产量 相应的P模型如下： Minimize ∑fy+∑∑c (7) subject to ∑=1 j=1,2,m (8) ∑%Dx,≤Ky i=1,2,.,n (9) X≤y (10) y=0or1i=1,2,.,n, (11) X=00r1i=1,2,.,nj=1,2,.m (12) 这是一个“单来源”版本问题。由于变量X被限制为0或1，每一个消费者必须将它的 全部消费需求固定在一个工厂。如果“多-来源”被允许的话，变量可以是分数，分数本 身表明消费者j在工厂i的消费比例。在这种情况下，条件(12)应该去掉。如果看重单来源， 就不希望有多来源。例如，在小学到中学的指派问题中，同一个小学的同学都希望去同样一 所中学。 6.2.6实例1 Zzyzx公司在下列城市分别有一个货栈：(A)Baltimore,(B)Cheyenne,.(C)Salt Lake City, (D)Memphis and(E)Wichita,这些货栈为全美国的消费者供货。我们将前美国的消费者集中 起来，认为他们分别在下列城市：(1)Atlanta,(2)Boston,.(3)Chicago,(4)Denver,(5)Omaha

个约束。然而，从经验上看，当用(3')代替(3)而将这个问题化成一个 LP 来求解时，解答自然 是整数。 6.2.5 能力受限制的工厂定位问题(CPL) 如果一个工厂把满足需求的数量作为重点考虑的因素，那么从 SPL 问题就会引出 CPL 问题。 特别地，CPL 问题假设每一个消费者的需求数量已知，每一个工厂生产的产品数量 受产品总量的限制。额外的参数定义如下： Dj = 消费者 j 的需求量， Ki = 定位于工地 i 工厂的产量 相应的 IP 模型如下： Minimize = =  = + n i n i m j i i ij ij f y c x 1 1 1 (7) subject to = = n i ij x 1 1 j = 1,2,.,m (8)  =  m j j ij i i D x K y 1 i = 1,2,.,n (9) xij≤yi (10) yi = 0 or 1 i = 1,2,.,n, (11) xij= 0 or l i = 1,2,.,n j = 1,2,.,m (12) 这是一个“单-来源”版本问题。由于变量 xij 被限制为 0 或 1，每一个消费者必须将它的 全部消费需求固定在一个工厂。 如果“多-来源”被允许的话，变量 xij 可以是分数，分数本 身表明消费者 j 在工厂 i 的消费比例。在这种情况下，条件(12)应该去掉。如果看重单来源， 就不希望有多来源。例如，在小学到中学的指派问题中，同一个小学的同学都希望去同样一 所中学。 6.2.6 实例 1 Zzyzx 公司在下列城市分别有一个货栈：(A) Baltimore, (B) Cheyenne, (C) Salt Lake City, (D) Memphis and (E) Wichita，这些货栈为全美国的消费者供货。我们将前美国的消费者集中 起来，认为他们分别在下列城市： (1) Atlanta, (2) Boston, (3) Chicago, (4) Denver, (5) Omaha

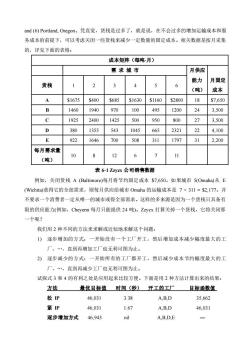
and(6)Portland,Oregon。凭直觉，货栈是过多了，就是说，在不会过多的增加运输成本和服 务成本的前提下，可以考虑关闭一些货栈来减少一定数量的固定成本。相关数据是按月采集 的，详见下面的表格： 成本矩阵（每吨-月） 需求城市 月供应 能力 月固定 货栈 2 3 5 6 (吨) 成本 A $1675 $400 $685 $1630 $1160 $2800 18 $7,650 B 1460 1940 970 100 495 1200 24 3,500 c 1925 2400 1425 500 950 800 27 3,500 D 380 1355 543 1045 665 2321 22 4.100 E 922 1646 700 508 311 1797 31 2.200 每月需求量 10 8 12 6 7 11 (吨) 表6-1Zyx公司销售数据 例如，关闭货栈A(Baltimore)每月将节约固定成本$7,650。如果城市5(Omaha)从E (Wichita)获得它的全部需求，则每月供应给城市Omaha的运输成本是7×31l=$2,177。并 不要求一个消费者一定从唯一的城市或得全部需求。这样的多来源是因为一个货栈只具备有 限的供应能力（例如，Cheyenn每月只能提供24吨）。Zyzx打算关掉一个货栈，它将关闭那 一个呢？ 我们用2种不同的方法来求解或近似地求解这个问题： 1)逐步增加的方式：一开始没有一个工厂开工，然后增加成本减少幅度最大的工 厂，.，直到再增加工厂也无利可图为止。 2)逐步减少的方式：一开始所有的工厂都开工，然后减少成本节约幅度最大的工 厂，.，直到再减少工厂也无利可图为止。 试探式3和4的有利之处是应用起来比较方便。下面是用2种方法计算出来的结果： 方法 最优目标值时间（秒） 开工的工厂目标函数值 松P 46,031 3.38 A,B,D 35,662 紧P 46,031 1.67 A,B,D 46,031 逐步增加方式 46.943 nil A,B,D,E

and (6) Portland, Oregon。凭直觉，货栈是过多了，就是说，在不会过多的增加运输成本和服 务成本的前提下，可以考虑关闭一些货栈来减少一定数量的固定成本。相关数据是按月采集 的，详见下面的表格： 成本矩阵（每吨-月） 需 求 城 市 月供应 能力 （吨） 月固定 成本 货栈 1 2 3 4 5 6 A $1675 $400 $685 $1630 $1160 $2800 18 $7,650 B 1460 1940 970 100 495 1200 24 3,500 C 1925 2400 1425 500 950 800 27 3,500 D 380 1355 543 1045 665 2321 22 4,100 E 922 1646 700 508 311 1797 31 2,200 每月需求量 （吨） 10 8 12 6 7 11 表 6-1 Zzyzx 公司销售数据 例如，关闭货栈 A (Baltimore)每月将节约固定成本 $7,650。如果城市 5(Omaha)从 E (Wichita)获得它的全部需求，则每月供应给城市 Omaha 的运输成本是 7 × 311 = $2,177。并 不要求一个消费者一定从唯一的城市或得全部需求。这样的多来源是因为一个货栈只具备有 限的供应能力(例如，Cheyenn 每月只能提供 24 吨)。Zzyzx 打算关掉一个货栈，它将关闭那 一个呢？ 我们用 2 种不同的方法来求解或近似地求解这个问题： 1) 逐步增加的方式：一开始没有一个工厂开工，然后增加成本减少幅度最大的工 厂，.，直到再增加工厂也无利可图为止。 2) 逐步减少的方式：一开始所有的工厂都开工，然后减少成本节约幅度最大的工 厂，.，直到再减少工厂也无利可图为止。 试探式 3 和 4 的有利之处是应用起来比较方便。下面是用 2 种方法计算出来的结果： 方法 最优目标值 时间（秒） 开工的工厂 目标函数值 松 IP 46,031 3.38 A,B,D 35,662 紧 IP 46,031 1.67 A,B,D 46,031 逐步增加方式 46,943 nil A,B,D,E —

逐步减少方式46,443 nil A,C,D,E 注意，尽管松P模型与紧P模型的最优解相等，但是，前者所用的计算时间是后者的 两倍。对于一个大型问题，这种差别将更加显著。对于紧P模型，相应的LP模型（去掉整 数变量的约束)的目标函数值与紧P模型的最优目标函数值相等。所以，紧P模型被当作 LP模型来求解的时候，得到的解答自然是整数。 单一产品的动态批量规模问题可以描述如下： n=一个产品计划生产的周期数： D=j周期预计的需求数量，j=1,2,.,n 6=产品在周期i生产的固定成本： h,=在周期i的单位产品库存到周期i+1的成本。 这个问题可以看成是一个简单工厂定位问题。我们定义： c=D,∑h 就是说，c时是用周期i的产品供应j期需求的成本。每个周期可以看成是一个工厂工地 和一个消费者。 更进一步，如果周期ⅰ只有有限的生产能力K,这时，能力受限的动态批量规模问题就 是一个特殊的能力受限制的工厂定位问题。 6.2.7表示具有一般阶梯状的成本曲线 在工厂定位问题中固定成本加线性变动成本曲线便是更加一般的阶梯状成本曲线（见下 面的图6-2)的一个特例。 三段斜率分别是C1,c2和c3。截距K2和K3是由公式K+1=K+CU:-c+1U确定。如果 C+1<C,则是一个具有规模效益经济活动的成本曲线。如果我们从一个供货商处购买商品时， 有数量规模折扣，就会有类似的成本曲线

逐步减少方式 46,443 nil A,C,D,E — 注意，尽管松 IP 模型与紧 IP 模型的最优解相等，但是，前者所用的计算时间是后者的 两倍。对于一个大型问题，这种差别将更加显著。对于紧 IP 模型，相应的 LP 模型（去掉整 数变量的约束）的目标函数值与紧 IP 模型的最优目标函数值相等。所以，紧 IP 模型被当作 LP 模型来求解的时候，得到的解答自然是整数。 单一产品的动态批量规模问题可以描述如下： n = 一个产品计划生产的周期数； Dj = j 周期预计的需求数量，j = 1, 2,.,n; fi = 产品在周期 i 生产的固定成本； hi = 在周期 i 的单位产品库存到周期 i + 1 的成本。 这个问题可以看成是一个简单工厂定位问题。我们定义： cij =  − = 1 1 j i Dj hi 就是说，cij 是用周期 i 的产品供应 j 期需求的成本。每个周期可以看成是一个工厂工地 和一个消费者。 更进一步，如果周期 i 只有有限的生产能力 Ki，这时，能力受限的动态批量规模问题就 是一个特殊的能力受限制的工厂定位问题。 6.2.7 表示具有一般阶梯状的成本曲线 在工厂定位问题中固定成本加线性变动成本曲线便是更加一般的阶梯状成本曲线（见下 面的图 6-2）的一个特例。 三段斜率分别是 c1, c2 和 c3。截距 K2 和 K3 是由公式 Ki+1 = Ki + ciUi - ci+1 Ui 确定。如果 ci+1 < ci, 则是一个具有规模效益经济活动的成本曲线。如果我们从一个供货商处购买商品时， 有数量规模折扣，就会有类似的成本曲线

案K K 60 U x 图6-2凹面分段线性成本曲线 表示这样的成本曲线有好几种方法。第1种方法就是前面表示一个固定成本加线性变动 成本曲线方法的推广。如果整个模型只有少数这样的曲线，而每个曲线只有一、两个转折点， 这个方法还是比较满意的。 定义： y=1如果U-1≤x<U,否则0 (a) x=X如果U1≤x<Ui,否则0 (b) 相应的模型应该包含下面的项目： MN=K*y1+K2*y2+K3*y3+C1*X1+C2*X2+C3*X3+.: 如果x在模型的其它地方出现，就可以用x1+发+x3取代。如果是01变量，那么上 面的约束确实正确表达了成本函数。如果成本曲线是凹面且关于ⅹ没有上限，那么约束集合 (b)就没有必要了。 6.2.8实例2 假设在一个大型问题中要确定向一个供货商订货（有数量折扣）的问题。情况是这样的： 一次订货的固定成本是$150。最初1,000加仑的产品每加仑价格是$2。超过1,000加仑的部 分每加仑的价格下降到$1.90。我们最多只能购买5,000加仑的产品。问题的各种参数计算如 下： K1=150: U1=1,000: K2=150+1,000×2-1,000×1.90=250: U2=5,000:

图 6-2 凹面分段线性成本曲线 表示这样的成本曲线有好几种方法。第 1 种方法就是前面表示一个固定成本加线性变动 成本曲线方法的推广。如果整个模型只有少数这样的曲线，而每个曲线只有一、两个转折点， 这个方法还是比较满意的。. 定义： yi =1 如果 Ui-1 ≤ x < Ui, 否则 0 (a) xi = x 如果 Ui-1 ≤ x < Ui, 否则 0 (b) 相应的模型应该包含下面的项目： MIN = Kl*y1 + K2*y2 + K3*y3 + C1*X1 + C2*X2 + C3*X3 +.； 如果 x 在模型的其它地方出现，就可以用 x1 + x2 + x3 取代。如果 yi 是 0/1 变量，那么上 面的约束确实正确表达了成本函数。如果成本曲线是凹面且关于 x 没有上限，那么约束集合 (b)就没有必要了。 6.2.8 实例 2 假设在一个大型问题中要确定向一个供货商订货（有数量折扣）的问题。情况是这样的： 一次订货的固定成本是$150。最初 1,000 加仑的产品每加仑价格是$2。超过 1,000 加仑的部 分每加仑的价格下降到$1.90。我们最多只能购买 5,000 加仑的产品。问题的各种参数计算如 下： K1 = 150; U1 = 1,000; K2 = 150 + 1,000 × 2 - 1,000 × 1.90 = 250; U2 = 5,000;

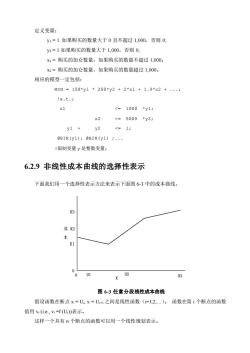
定义变量： y1=1如果购买的数量大于0且不超过1,000，否则0： y2=1如果购买的数量大于1,000，否则0： x1=购买的加仑数量，如果购买的数量不超过1,000： X2=购买的加仑数量，如果购买的数量超过1,000。 相应的模型一定包括： MIN=150*y1*250*y2+2*x1+1.9*x2+.; !s.t.; x1 <=1000 *y1; x2 <=5000 *y2; y1+ y2 <=1; @BIN(y1);eBIN(y1);.·· !限制变量y是整数变量： 6.2.9非线性成本曲线的选择性表示 下面我们用一个选择性表示方法来表示下面图6-3中的成本曲线。 K3 成K2 0 Ui X U2 U3 图6-3任意分段线性成本曲线 假设函数在断点X=U,x=U+1之间是线性函数(=1,2，.)。函数在第i个断点的函数 值用v:(i.e.,v=f(U)表示。 这样一个具有个断点的函数可以用一个线性规划表示

定义变量： y1 = 1 如果购买的数量大于 0 且不超过 1,000，否则 0; y2 = 1 如果购买的数量大于 1,000，否则 0; x1 = 购买的加仑数量，如果购买的数量不超过 1,000； x2 = 购买的加仑数量，如果购买的数量超过 1,000。 相应的模型一定包括： MIN = 150*yl * 250*y2 + 2*xl + 1.9*x2 + .; !s.t.; x1 <= 1000 *y1; x2 <= 5000 *y2; y1 + y2 <= 1; @BIN(y1); @BIN(y1) ;. !限制变量 y 是整数变量; 6.2.9 非线性成本曲线的选择性表示 下面我们用一个选择性表示方法来表示下面图 6-3 中的成本曲线。 图 6-3 任意分段线性成本曲线 假设函数在断点 x = Ui, x = Ui+1 之间是线性函数（i=1,2,.）。 函数在第 i 个断点的函数 值用 vi (i.e., vi =f (Ui))表示。 这样一个具有 n 个断点的函数可以用一个线性规划表示

1)增加约束：w1+w2+.+wa=1 2)用下面的表达式替换任何一个x的值： WIU1+W2U2++WnUn 3)用下面的表达式替换任何一个(x)的值： W1V1+W2V2++WnVn 4)最多只允许有两个不等于0且相邻w的值，其它的值都是0。 新变量w指定了点U的权数。如果函数f(x)在两个相邻的点X=U:和x=UH之间 是线性函数，x=wU+w+1U+1满足w+w+1=1,那么，fx)=wU)+W+1fU+1)=wV+ Wi+l Vi+lo 可以用数种方法形成约束(4)。约束(1)可以用一些P代码表示，就是所谓的“第2类特 殊命令集合”或简称“SOS2”。对于用$OS2表示的每一个约束将自动满足约束(4)。 如果我们有一个标准的P代码，而没有SOS2特征，那么约束(4)可以用下面一系列约束 表示： WI ≤z1 W2 ≤Z1+Z2 W3≤Z2+Z3 wn-1≤Zn-2+Zn-l Wn ≤zn-1 Z1+Z2+.+Zn-=1 Zi=0or 1. 总结如下，处理一个非线性项目需要一个约束和n个变量。如果没有SOS2特征，处理 一个非线性项目必须增加n个约束和n-1个变量。 这里描述的一般方法有时称为拉姆达方法。 6.2.10将乘积函数转换成分离函数 前面介绍的方法只能是用来处理一个变量的非线性函数。还有一些标准的方法可以用来 转换一个多变量函数，所以，一个函数也可以利用转换变量用分离的形式表示。最普通的转

1) 增加约束：w1+ w2 +. + wn = 1 2) 用下面的表达式替换任何一个 x 的值： w1U1+ w2U2+.+ wnUn 3) 用下面的表达式替换任何一个 f(x)的值: w1v1+ w2v2+.+ wnvn 4) 最多只允许有两个不等于 0 且相邻 wi 的值，其它的值都是 0。 新变量 wi 指定了点 Ui 的权数。如果函数 f(x)在两个 相邻的点 x = Ui 和 x = Ui+l 之间 是线性函数，x = wiUi+ wi+1Ui+1 满足 wi + wi.+1 = 1，那么，f(x) = wif(Ui) + wi+1f(Ui+1 ) = wivi+ wi+1vi+1。 可以用数种方法形成约束(4)。约束(1)可以用一些 IP 代码表示，就是所谓的“第 2 类特 殊命令集合”或简称“SOS2”。对于用 SOS2 表示的每一个约束将自动满足约束(4)。 如果我们有一个标准的 IP 代码，而没有 SOS2 特征，那么约束(4)可以用下面一系列约束 表示： w1 ≤ z1 w2 ≤ z1 + z2 w3 ≤ z2 + z3 . . . wn-1 ≤ zn-2 + zn-1 wn ≤ zn- 1 z1 + z2 + . + zn-l = 1 zi = 0 or 1. 总结如下，处理一个非线性项目需要一个约束和 n 个变量。如果没有 SOS2 特征，处理 一个非线性项目必须增加 n 个约束和 n – 1 个变量。 这里描述的一般方法有时称为拉姆达方法。 6.2.10 将乘积函数转换成分离函数 前面介绍的方法只能是用来处理一个变量的非线性函数。还有一些标准的方法可以用来 转换一个多变量函数，所以，一个函数也可以利用转换变量用分离的形式表示。最普通的转