安徽大学：《运筹学》课程理论教案（PPT讲稿）第五章 整数规划

第五章 整数规划 整数规划及其数学模型 用分支定界法求解整数规划 0-1型整数规划 指派问题 3

3 第五章 整 数 规 划 整数规划及其数学模型 用分支定界法求解整数规划 0-1型整数规划 指派问题

第一节整数规划及其数学模型 整数规划数学模型的一般形式 要求一部分或全部决策变量必须取整数值的 规划问题称为整数规划(integer programming, 简记IP)。不考虑整数条件，由余下的目标函数 和约束条件构成的规划问题称为该整数规划问题 的松弛问题(slack problem)。若松弛问题是 个线性规则，则称该整数规划为整数线性规划 (integer linear programming)。整数线性规划 数学模型的一般形式为：

4 一、 整数规划数学模型的一般形式 要求一部分或全部决策变量必须取整数值的 规划问题称为整数规划(integer programming， 简记IP)。不考虑整数条件，由余下的目标函数 和约束条件构成的规划问题称为该整数规划问题 的松弛问题(slack problem)。若松弛问题是一 个线性规则，则称该整数规划为整数线性规划 (integer linear programming)。整数线性规划 数学模型的一般形式为： 第一节 整数规划及其数学模型

第一节整数规划及其数学模型 OptZ=cix1+c2x2+.+cnxm (1-1) ak+a2x2+.+anXn≤ (=,≥) b a21X1+a222+.+a2nXn≤ (=,2) b2 (1-2) am+am22.+amnn ≤ (=,2) x,部分或全部取整(i=1,2,.,n) 5

5 第一节 整数规划及其数学模型 Opt Z = c1 x1 + c2 x2 + . + cn xn (1-1) 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 1, 2, , ) ( , ) ( , ) . ( , ) n n n n m m mn n m i i n a x a x a x b a x a x a x b a x a x a x b x =  + ++  =   + ++  =      + ++  =    部分或全部取整（ (1-2)

第一节整数规划及其数学模型 整数线性规划问题分为下列几种类型： 1.纯整数线性规划：指全部决策变量部必 须取整数值的整数线性规划。有时，也称为全 整数规划 2.混合整数线性规划：指决策变量中有 一部分必须取整数值，另一部分可以不取整数 值的整数线性规划 3.0-1型整数线性规划：指决策变量只能 取值0或1的整数线性规划

6 整数线性规划问题分为下列几种类型： 1．纯整数线性规划：指全部决策变量部必 须取整数值的整数线性规划。有时，也称为全 整数规划。 2．混合整数线性规划：指决策变量中有 一部分必须取整数值，另一部分可以不取整数 值的整数线性规划。 3．0-1型整数线性规划：指决策变量只能 取值0或1的整数线性规划。 第一节 整数规划及其数学模型

第一节整数规划及其数学模型 本章仅讨论整数线性规划。后面提到的整数 规划，一般都是指整数线性规划 整数规划的实例很多。例如，我们前面介绍 的生产问题，如果产量的单位是件，则往往就要 求变量取整数。另外，在表示工厂何时开工等问 题时，往往需要利用0-1型整数变量 整数规划解的特点 整数线性规划及其松弛问题，从解的特点上 看，二者之间既有密切的联系，又有本质区别

7 本章仅讨论整数线性规划。后面提到的整数 规划，一般都是指整数线性规划。 整数规划的实例很多。例如，我们前面介绍 的生产问题，如果产量的单位是件，则往往就要 求变量取整数。另外，在表示工厂何时开工等问 题时，往往需要利用0-1型整数变量。 二、 整数规划解的特点 整数线性规划及其松弛问题，从解的特点上 看，二者之间既有密切的联系，又有本质区别。 第一节 整数规划及其数学模型

第一节整数规划及其数学模型 松弛问题作为一个线性规划问题，其可行解 的集合是一个凸集，任意两个可行解的凸组合仍 为可行解。整数规划问题的可行解集合是它的松 弛问题可行解集合的一个子集，任意两个可行解 的凸组合不一定满足整数约束条件，因而不一定 仍为可行解。由于整数规划问题的可行解一定也 是它的松弛问题的可行解（反之则不一定），所 以，整数规划问题最优解的目标函数值不会优于 松弛问题最优解的目标函数值

8 松弛问题作为一个线性规划问题，其可行解 的集合是一个凸集，任意两个可行解的凸组合仍 为可行解。整数规划问题的可行解集合是它的松 弛问题可行解集合的一个子集，任意两个可行解 的凸组合不一定满足整数约束条件，因而不一定 仍为可行解。由于整数规划问题的可行解一定也 是它的松弛问题的可行解（反之则不一定），所 以，整数规划问题最优解的目标函数值不会优于 松弛问题最优解的目标函数值。 第一节 整数规划及其数学模型

第一节整数规戈划及其数学模型 在一般情况下，松弛问题的最优解不会刚好 满足变量的整数约束条件，因而不是整数规划的 可行解，自然就不是整数规划的最优解。此时， 若对松弛问题的这个最优解中不符合整数要求的 分量简单地取整数，所得到的解不一定是整数规 划问题的最优解，甚至还不一定是整数规划问题 的可行解

9 在一般情况下，松弛问题的最优解不会刚好 满足变量的整数约束条件，因而不是整数规划的 可行解，自然就不是整数规划的最优解。此时， 若对松弛问题的这个最优解中不符合整数要求的 分量简单地取整数，所得到的解不一定是整数规 划问题的最优解，甚至还不一定是整数规划问题 的可行解。 第一节 整数规划及其数学模型

第一节整数规划及其数学模型 例1考虑下面的整数规划问题 max Z=x+4x2 -2x1+3x2≤3 x1+2x2≤8 x1x2 ≥0且取整数 画出可行域见图41。在图4-1中，四边形 OBPC及其内部的点为松弛问题的可行域，其中 那些整数格点为整数规划问题的可行解。根据目 标函数等值线的优化方向，P点(x=187, x2=19/7)就是其松弛问题的最优解，z=94/7

10 画出可行域见图4-1 。在图4-1中，四边形 OBPC及其内部的点为松弛问题的可行域，其中 那些整数格点为整数规划问题的可行解。根据目 标函数等值线的优化方向 ， P 点 （ x1 =18/7, x2 =19/7）就是其松弛问题的最优解，z＝94/7。       +  − +  = + , 0且取整数 2 8 2 3 3 max 4 1 2 1 2 1 2 1 2 x x x x x x Z x x 例1 考虑下面的整数规划问题： 第一节 整数规划及其数学模型

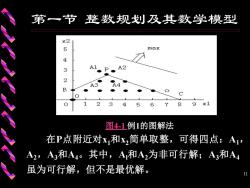
第一节整数规划及其数学模型 x2 5 max 4 3 A2 2 B 9 x1 图41例1的图解法 在P点附近对x和x简单取整，可得四点：A1, A2,A3和A4。其中，A和A2为非可行解；A3和A4 虽为可行解，但不是最优解

11 在P点附近对x1和x2简单取整，可得四点：A1， A2，A3和A4。其中，Al和A2为非可行解；A3和A4 虽为可行解，但不是最优解。 图4-1 例1的图解法 第一节 整数规划及其数学模型

第一节整数规划及其数学模型 本例整数规划的最优解为A*点（区1=4，x22) 其目标函数值Z=12。 由于整数规划及其松弛问题之间的上述特殊 关系，像例4先求松驰问题最优解，再用简单取整 的方法虽然直观简单，却并不是求解整数规划的 有效方法。 12

12 本例整数规划的最优解为A*点(x1 ＝4，x2 =2)， 其目标函数值Z =12。 由于整数规划及其松弛问题之间的上述特殊 关系，像例4先求松弛问题最优解，再用简单取整 的方法虽然直观简单，却并不是求解整数规划的 有效方法。 第一节 整数规划及其数学模型