《运筹学》课程教学资源（参考资料）7 随机规划模型

7随机规划模型 7.1引言 多期计划很困难的主要理由就是未来的情况不确定。一般来说，我们今天要做的某个行 为或决策应该是未来可能出现各种情况下最好决策的一个折衷。例如，如你预计下一年产品 需求量可能很大，而且原材料价格将迅速上涨，那么，你今天购买大量原材料以备下一年使 用的举动就是一个明智和理性的决策。然而另一方面，如果万一下一年的产品和原材料市场 都消失了，那么，公司的股东决不会认为你的行为只是运气不好而己。 7.2不确定举例 在现实问题中，我们常常会遇到一些典型的不确定情况，现举例如下： 1)与气候有关的不确定情况： ●要为即将到来的冬季决定存储汽油的数量和地点： ●考虑到水力发电、航运和灌溉，要决定春天的放水计划。 2)与金融有关的不确定情况： ●市场价格的变动（例如，股票价格，投资利率和汇率的变动）： ●贸易伙伴的消失（例如，主要客户的破产）。 3)与政治有关的不确定情况： ·政府的更迭： ●敌意的爆发。 4)与技术有关的不确定情况： ●一种新技术何时被采用要等到下一代产品列入计划才可以确定。 5)与行情有关的不确定情况： ●品味与时尚的转移 ●人口的移动

1 7 随机规划模型 7.1 引言 多期计划很困难的主要理由就是未来的情况不确定。一般来说，我们今天要做的某个行 为或决策应该是未来可能出现各种情况下最好决策的一个折衷。例如，如你预计下一年产品 需求量可能很大，而且原材料价格将迅速上涨，那么，你今天购买大量原材料以备下一年使 用的举动就是一个明智和理性的决策。然而另一方面，如果万一下一年的产品和原材料市场 都消失了，那么，公司的股东决不会认为你的行为只是运气不好而已。 7.2 不确定举例 在现实问题中，我们常常会遇到一些典型的不确定情况，现举例如下： 1）与气候有关的不确定情况: ⚫ 要为即将到来的冬季决定存储汽油的数量和地点； ⚫ 考虑到水力发电、航运和灌溉，要决定春天的放水计划。 2）与金融有关的不确定情况: ⚫ 市场价格的变动(例如，股票价格，投资利率和汇率的变动)； ⚫ 贸易伙伴的消失(例如，主要客户的破产)。 3）与政治有关的不确定情况: ⚫ 政府的更迭; ⚫ 敌意的爆发。 4）与技术有关的不确定情况: ⚫ 一种新技术何时被采用要等到下一代产品列入计划才可以确定。 5）与行情有关的不确定情况: ⚫ 品味与时尚的转移; ⚫ 人口的移动

2 6)与竞争有关的不确定情况： 。为下一年的竞争而准备的各种策略。 7)与不可抗拒力有关的不确定情况 ·可能的飓风，龙卷风，地震和火灾， ●可能的设备故障。 在不确定决策分析的过程中，我们首先要鉴别哪些项目与我们的决策有关（例如上边列 出的项目)。在特殊情况下，气候也可以是一个大的不确定源。例如，有报告说：某个水电 站在以后的3年内，由于降雨量的变化使得每年的发电量可以从8,350亿瓦小时下降到2,100 亿瓦小时。 在汽车工业和公共事业领域也会出现不确定情况。由于未来需求不确定，汽车工业就面 临着要对下属的工厂做出开或关的决定。在公共事业方面，由于未来气候不确定，政府要为 以后数年购买多少燃料做出决定。 7.3状态方法 我们首先来研究一个2周期的计划问题，这类问题需要分3个步骤来完成： 步骤1：做出第1期决策。 步骤2：自然地（就如同市场情况一样常常知道结果）做出一个随机决策。 步骤3：根据(2)做出第2期决策。该决策试图改善最坏的结果。 状态方法假定：自然地做出随机决定的数目是有限的。我们称可能出现的自然情况称为 “状态”。例如，在实践中，多数人愿意将产品的需求分为低、中、高3个状态：或者愿意 将冬季分为严冬、正常、暖冬3个状态，而不愿意用60个地点的日平均温度或降雪量取而 代之。历史上，通用汽车公司就使用低、中、高3个状态来描述需求的不确定性。如果一 个LP模型含有不确定性，那么就称这个LP模型是一个“随机规划”。 下面介绍本章的第1个例子。在对这个例子进行分析的过程中，步骤(1)和(2)非常重要。 例1假设有一个农民可以在他的地里种植玉米、高粱或大豆。他愿意将种植季节化分为 旱季和雨季。为了简单起见，我们假设他的划分成立。就是说除了旱季和雨季，不会出现其 它的情况。如果出现雨季，种植玉米的利润多一些：否则，种植高粱的利润多一些。具体的 数据可以从下面的表格中得到： 利润亩（迭策的函数）

2 6) 与竞争有关的不确定情况: ⚫ 为下一年的竞争而准备的各种策略。 7) 与不可抗拒力有关的不确定情况: ⚫ 可能的飓风，龙卷风，地震和火灾; ⚫ 可能的设备故障。 在不确定决策分析的过程中，我们首先要鉴别哪些项目与我们的决策有关（例如上边列 出的项目）。在特殊情况下，气候也可以是一个大的不确定源。例如，有报告说：某个水电 站在以后的3年内，由于降雨量的变化使得每年的发电量可以从 8,350 亿瓦小时下降到2,100 亿瓦小时。 在汽车工业和公共事业领域也会出现不确定情况。由于未来需求不确定，汽车工业就面 临着要对下属的工厂做出开或关的决定。在公共事业方面，由于未来气候不确定，政府要为 以后数年购买多少燃料做出决定。 7.3 状态方法 我们首先来研究一个 2 周期的计划问题，这类问题需要分 3 个步骤来完成： 步骤 1：做出第 1 期决策。 步骤 2：自然地 (就如同市场情况一样常常知道结果)做出一个随机决策。 步骤 3：根据（2）做出第 2 期决策。该决策试图改善最坏的结果。 状态方法假定：自然地做出随机决定的数目是有限的。我们称可能出现的自然情况称为 “状态”。例如，在实践中，多数人愿意将产品的需求分为低、中、高 3 个状态；或者愿意 将冬季分为严冬、正常、暖冬 3 个状态，而不愿意用 60 个地点的日平均温度或降雪量取而 代之。 历史上，通用汽车公司就使用低、中、高 3 个状态来描述需求的不确定性。如果一 个 LP 模型含有不确定性，那么就称这个 LP 模型是一个“随机规划”。 下面介绍本章的第 1 个例子。在对这个例子进行分析的过程中，步骤(1)和(2)非常重要。 例 1 假设有一个农民可以在他的地里种植玉米、高粱或大豆。他愿意将种植季节化分为 旱季和雨季。为了简单起见，我们假设他的划分成立。就是说除了旱季和雨季，不会出现其 它的情况。如果出现雨季，种植玉米的利润多一些；否则，种植高粱的利润多一些。具体的 数据可以从下面的表格中得到： 利润/亩（决策的函数）

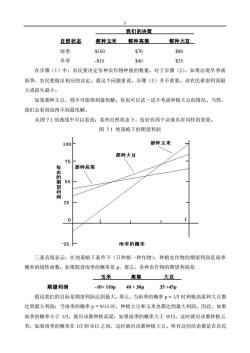
3 我们的迭策 自然状态 都种玉米 都种高粱 都种大豆 雨季 $100 $70 $80 旱季 -$10 $40 $35 在步骤(1)中，农民要决定各种农作物种植的数量。对于步骤(2)，如果出现旱季或 雨季，农民要做出相应的决定。就这个问题来说，步骤(3)并不重要。该农民希望利润最 大或损失最小。 如果都种大豆，则不可能得到最优解。你也可以试一试不考虑种植大豆的情况。当然， 我们会看到也得不到最优解。 从图71的曲线中可以看到：某些自然状态下，恰好有两个决策具有同样的效果。 图7.1纯策略下的期望利润 100 都种玉米 都种大豆 75 每亩的 都种高粱 50 润 25 0 -25 雨季的概率 三条直线表示：在纯策略下条件下（只种植一种作物），种植农作物的期望利润是雨季 概率的线性函数。如果假设雨季的概率是，那么，各种农作物的期望利润是： 玉米 高粱 大豆 期望利润 -10+110p40+30p 35+45p 假设我们的目标是期望利润达到最大。那么，当雨季的概率p=1/3时种植高粱和大豆都 达到最大利润：当雨季的概率p=9/13时，种植大豆和玉米也都达到最大利润。因此，如果 雨季的概率小于13，就应该都种植高粱：如果雨季的概率大于913，这时就应该都种植玉 米：如果雨季的概率在13到9/13之间，这时就应该都种植大豆。所有这些结论都是在农民

3 我们的决策 自然状态 都种玉米 都种高粱 都种大豆 雨季 $100 $70 $80 旱季 -$10 $40 $35 在步骤（1）中，农民要决定各种农作物种植的数量。对于步骤（2），如果出现旱季或 雨季，农民要做出相应的决定。就这个问题来说，步骤（3）并不重要。该农民希望利润最 大或损失最小。 如果都种大豆，则不可能得到最优解。你也可以试一试不考虑种植大豆的情况。当然， 我们会看到也得不到最优解。 从图 7.1 的曲线中可以看到：某些自然状态下，恰好有两个决策具有同样的效果。 图 7.1 纯策略下的期望利润 三条直线表示：在纯策略下条件下（只种植一种作物），种植农作物的期望利润是雨季 概率的线性函数。如果假设雨季的概率是 p，那么，各种农作物的期望利润是: 玉米 高粱 大豆 期望利润 -10+ 110p 40 + 30p 35 +45p 假设我们的目标是期望利润达到最大。那么，当雨季的概率 p = 1/3 时种植高粱和大豆都 达到最大利润；当雨季的概率 p = 9/13 时，种植大豆和玉米也都达到最大利润。因此，如果 雨季的概率小于 1/3，就应该都种植高粱；如果雨季的概率大于 9/13，这时就应该都种植玉 米；如果雨季的概率在 1/3 到 9/13 之间，这时就应该都种植大豆。所有这些结论都是在农民

只对最大利润感兴趣而不考虑风险问题这一假设基础之上而得到的。就是说，如果农民只追 求利润最大，那么，最优策略一定是一个纯策略：都种植玉米，或都种植高粱，或都种植大 豆。 针对可能出现的各种自然状态，人们也许试着用“条件最优”决策的加权平均来进行第 1期的决策。对于这个例子，如果我们知道自然状态是雨季，最优解就是都种植玉米：如果 我们知道自然状态是旱季，最优解就是都种植高粱。假设雨季的概率是3/8。因此，"加权" 的决策是每亩种植3/8的玉米和5/8的高粱。这时，每亩的期望利润是(3/8)(3/8)100+(5/8)70] +(5/8)[(3/8)(-10)+(5/8)40]=$43.75 我们将这个结果与期望利润最大的决策进行比较。如果雨季的概率等于3/8，每亩都种 植大豆的期望利润是(3/8)80+(5/8)35=$51.875。这个最优值比前面所谓的“合理”结果多 20%。 从这个例子中，我们可以得到下面实质性的结论： 如果未来有多种状态，今天的最优决策一般情况下不等于各种状态下最 优决策的“加权平均”。 对于这个简单的问题，人们并非一定要用LP求解。然而，为了今后处理更为复杂的问 题，我们还是用LP来演示一下。这里，第1期有3个决策变量： C=玉米种植的数量（亩）， S=高粱种植的数量（亩）， B=大豆种植的数量（亩）。 假设未来出现雨季的概率为3/8，目标函数是： Maximize(3/8)(100c+70s+80B)+(5/8)(-10c+40S+35B) subject to C+s B <1 上面唯一的约束是表示：我们只考虑在一亩地里种植何种作物。将目标函数简化，就得 到： Maximize31.25c+51.25S+51.875B subject to C+S+B<=1。 解答是B=1(就是都种植大豆)。 注意，目标函数中玉米和高粱的系数分别是相应作物的期望利润（每亩）

4 只对最大利润感兴趣而不考虑风险问题这一假设基础之上而得到的。就是说，如果农民只追 求利润最大，那么，最优策略一定是一个纯策略：都种植玉米，或都种植高粱，或都种植大 豆。 针对可能出现的各种自然状态，人们也许试着用“条件最优”决策的加权平均来进行第 1 期的决策。对于这个例子，如果我们知道自然状态是雨季，最优解就是都种植玉米；如果 我们知道自然状态是旱季，最优解就是都种植高粱。假设雨季的概率是 3/8。因此，"加权" 的决策是每亩种植 3/8 的玉米和 5/8 的高粱。这时，每亩的期望利润是(3/8)[(3/8)100 + (5/8)70] + (5/8) [(3/8)(-10) + (5/8)40] = $43.75. 我们将这个结果与期望利润最大的决策进行比较。如果雨季的概率等于 3/8，每亩都种 植大豆的期望利润是(3/8)80 + (5/8)35 = $51.875。这个最优值比前面所谓的“合理”结果多 20%。 从这个例子中，我们可以得到下面实质性的结论： 如果未来有多种状态，今天的最优决策一般情况下不等于各种状态下最 优决策的“加权平均”。 对于这个简单的问题，人们并非一定要用 LP 求解。然而，为了今后处理更为复杂的问 题，我们还是用 LP 来演示一下。这里，第 1 期有 3 个决策变量： C = 玉米种植的数量（亩）， S = 高粱种植的数量（亩）， B = 大豆种植的数量（亩）。 假设未来出现雨季的概率为 3/8，目标函数是： Maximize (3/8)(100C + 70S + 80B) + (5/8)(-10C + 40S + 35B) subject to C + S + B <= 1 上面唯一的约束是表示：我们只考虑在一亩地里种植何种作物。将目标函数简化，就得 到： Maximize 31.25 C + 51.25 S + 51.875 B subject to C + S + B <= 1。 解答是 B = 1 (就是都种植大豆)。 注意，目标函数中玉米和高粱的系数分别是相应作物的期望利润（每亩）

7.4一个更为复杂的2周期计划问题 在前面的例子中，第2期决策不是很重要。自然状态给出后，相应的决策显而易见。 然而在下面的例子中，就需要做出第2期的决策。 例2假设某个北方城市已经到了夏季的后期（假设没有秋季）。道路主管要为即将来到 的冬季购买清除道路积雪用的燃料和食盐。如果出现严冬，燃料和食盐未必能保证供应，而 且价格可能要上涨。清除道路积雪有两种方法：一种方法是铲雪，一种方法是撒盐。相对来 说，撒盐要便宜一些，尤其是在暖冬季节更是如此。然而，暖冬季节之后，多余的食盐一定 要等到下一个冬季来临才能使用，而多余的燃料可以用做它用，无须存储到下一个冬季。所 以，如果准备的燃料多了也不会造成太大的浪费。 道路主管愿意将冬季分为暖冬和严冬，并假设暖冬和严冬出现的概率分别为0.4和0.6。 在下面的表格里列出了食盐和燃料的成本和回收价值。在冬季之前就要做第1期决策，在冬 季来临之后就要做第2期决策。为读者方便，所有的数据都用“车天”表示。1“车天”就 是一辆清雪车一天的费用。 成本或价值 食盐 燃料 成本/车天 第1期购买 S20 S70 第2期购买 暖 S30 S73 S110 寒 S32 S73 $120 第2期末的回收价值 S15 S65 注意，食盐第2期的价格是一个随机变量（取决于气候）。如果冬季寒冷，我们预计食 盐的价格将会上涨。 在暖冬季节，每天出动一辆车的成本（除了燃料和食盐）是$110，而在严冬季节是$120。 整个冬季可以出动的车天数为5,000。如果只是铲雪，一个暖冬除雪大约需要3,500车天：而 一个严冬除雪大约需要5,100车天。一般来说，撒盐除雪的效率要高一点。在暖冬，一辆清 雪车撒盐除雪的效率是铲雪的1.2倍：在严冬，一辆清雪车撒盐除雪的效率是铲雪的1.1倍。 所以，在严冬季节，必须有一定数量的清雪车从事撒盐除雪。 下面定义各个时间段的变量： BF1=第1期购买燃料的数量（车天） BS1=第1期购买食盐的数量（车天）：

5 7.4 一个更为复杂的 2 周期计划问题 在前面的例子中， 第 2 期决策不是很重要。自然状态给出后，相应的决策显而易见。 然而在下面的例子中，就需要做出第 2 期的决策。 例 2 假设某个北方城市已经到了夏季的后期（假设没有秋季）。道路主管要为即将来到 的冬季购买清除道路积雪用的燃料和食盐。如果出现严冬，燃料和食盐未必能保证供应，而 且价格可能要上涨。清除道路积雪有两种方法：一种方法是铲雪，一种方法是撒盐。相对来 说，撒盐要便宜一些，尤其是在暖冬季节更是如此。然而，暖冬季节之后，多余的食盐一定 要等到下一个冬季来临才能使用，而多余的燃料可以用做它用，无须存储到下一个冬季。所 以，如果准备的燃料多了也不会造成太大的浪费。 道路主管愿意将冬季分为暖冬和严冬，并假设暖冬和严冬出现的概率分别为 0.4 和 0.6。 在下面的表格里列出了食盐和燃料的成本和回收价值。在冬季之前就要做第 1 期决策，在冬 季来临之后就要做第 2 期决策。为读者方便，所有的数据都用“车天”表示。1“车天”就 是一辆清雪车一天的费用。 成本 或 价值 食盐 燃料 成本/车天 第 1 期购买 $20 $70 第 2 期购买 暖 $30 $73 $110 寒 $32 $73 $120 第 2 期末的回收价值 $15 $65 注意，食盐第 2 期的价格是一个随机变量（取决于气候）。如果冬季寒冷，我们预计食 盐的价格将会上涨。 在暖冬季节，每天出动一辆车的成本（除了燃料和食盐）是$110，而在严冬季节是$120。 整个冬季可以出动的车天数为 5,000。如果只是铲雪，一个暖冬除雪大约需要 3,500 车天；而 一个严冬除雪大约需要 5,100 车天。一般来说，撒盐除雪的效率要高一点。在暖冬，一辆清 雪车撒盐除雪的效率是铲雪的 1.2 倍；在严冬，一辆清雪车撒盐除雪的效率是铲雪的 1.1 倍。 所以，在严冬季节，必须有一定数量的清雪车从事撒盐除雪。 下面定义各个时间段的变量： BF1 = 第 1 期购买燃料的数量（车天） BS1 = 第 1 期购买食盐的数量（车天）；

6 BFW=暖冬情况下，第2期购买燃料的数量： BSW=暖冬情况下，第2期购买食盐的数量： XFW=暖冬末剩余燃料的数量： XSW=暖冬末剩余食盐的数量： PW=暖冬情况下，铲雪的数量（车天）： SW=暖冬情况下，撒盐的数量（车天）： KW=暖冬季节投入的成本（美元）： BFC=严冬情况下，第2期购买燃料的数量： BSC=严冬情况下，第2期购买食盐的数量： XFC=严冬末剩余燃料的数量： XSC=严冬末剩余食盐的数量： PC=严冬情况下，铲雪的数量（车天）： SC=严冬情况下，撒盐的数量（车天）： KC=严冬季节投入的成本（美元） 特别注意，我们针对第2期可能出现的每一种自然状态，定义了相应的决策变量（例如， 第2期购买燃料的数量取决于是暖冬还是严冬)。这也是建立模型的关键所在。 7.4.1暖冬解答 如果出现暖冬，相应的LP模型如下： MODEL: MIN 70 BF1 20 BS1 KW; -BF1 BFW XFW PW SW =0; !(燃料约束)： -BS1 BSW XSW SW 0; ！(食盐约束)： PW+sW3500: !(除雪约束)： KW-73*BFW-30*BSW+65*XEW+15*XSW!(成本约束)： -110*PW-110*SW=0: END 相应的解答是： Global optimal solution found at step: 2

6 BFW = 暖冬情况下，第 2 期购买燃料的数量； BSW = 暖冬情况下，第 2 期购买食盐的数量； XFW = 暖冬末剩余燃料的数量； XSW = 暖冬末剩余食盐的数量； PW = 暖冬情况下，铲雪的数量（车天）； SW = 暖冬情况下，撒盐的数量（车天）； KW = 暖冬季节投入的成本（美元）； BFC = 严冬情况下，第 2 期购买燃料的数量； BSC = 严冬情况下，第 2 期购买食盐的数量； XFC = 严冬末剩余燃料的数量； XSC = 严冬末剩余食盐的数量； PC = 严冬情况下，铲雪的数量（车天）； SC = 严冬情况下，撒盐的数量（车天）； KC = 严冬季节投入的成本（美元） 特别注意，我们针对第 2 期可能出现的每一种自然状态，定义了相应的决策变量（例如， 第 2 期购买燃料的数量取决于是暖冬还是严冬）。这也是建立模型的关键所在。 7.4.1 暖冬解答 如果出现暖冬，相应的 LP 模型如下： MODEL: MIN = 70 * BF1 + 20 * BS1 + KW; -BF1 - BFW + XFW + PW + SW = 0; !(燃料约束); -BS1 - BSW + XSW + SW = 0; !(食盐约束); PW + SW 3500; !(除雪约束); KW - 73*BFW - 30*BSW + 65*XFW + 15*XSW !(成本约束); - 110 * PW - 110 * SW = 0; END 相应的解答是： Global optimal solution found at step: 2

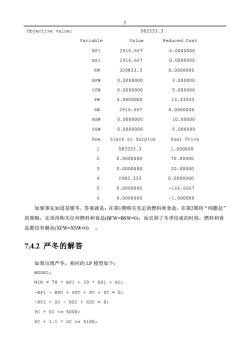
Objective value: 583333.3 Variable Value Reduced Cost BF1 2916.667 0.0000000 BS1 2916.667 0.0000000 KW 320833.3 0.0000000 BEW 0.0000000 3.000000 XFW 0.0000000 5.000000 PW 0.0000000 13.33333 SW 2916.667 0.0000000 BSW 0.0000000 10.00000 XSW 0.0000000 5.000000 Row slack or Surplus Dual Price 1 583333.3 1.000000 0.0000000 70.00000 3 0.0000000 20.00000 2083.333 0.0000000 0.0000000 -166.6667 6 0.0000000 -1.000000 如果事先知道是暖冬，答案就是：在第1期购买充足的燃料和食盐，在第2期用“纯撒盐” 的策略，无须再购买任何燃料和食盐(BFW=BSW=O),而且到了冬季结束的时候，燃料和食 盐都没有剩余(XFW=XSW=O)。 7.4.2严冬的解答 如果出现严冬，相应的LP模型如下： MODEL: MIN 70 BF1 20 BS1 KC; -BF1 BFC XFC PC SC 0; -BS1 SC BSC XSC =0; PC+sc=5100:

7 Objective value: 583333.3 Variable Value Reduced Cost BF1 2916.667 0.0000000 BS1 2916.667 0.0000000 KW 320833.3 0.0000000 BFW 0.0000000 3.000000 XFW 0.0000000 5.000000 PW 0.0000000 13.33333 SW 2916.667 0.0000000 BSW 0.0000000 10.00000 XSW 0.0000000 5.000000 Row Slack or Surplus Dual Price 1 583333.3 1.000000 2 0.0000000 70.00000 3 0.0000000 20.00000 4 2083.333 0.0000000 5 0.0000000 -166.6667 6 0.0000000 -1.000000 如果事先知道是暖冬，答案就是：在第1期购买充足的燃料和食盐，在第2期用“纯撒盐” 的策略，无须再购买任何燃料和食盐(BFW=BSW=0)，而且到了冬季结束的时候，燃料和食 盐都没有剩余(XFW=XSW=0) 。 7.4.2 严冬的解答 如果出现严冬，相应的 LP 模型如下： MODEL: MIN = 70 * BF1 + 20 * BS1 + KC; -BF1 - BFC + XFC + PC + SC = 0; -BS1 + SC - BSC + XSC = 0; PC + SC = 5100;

8 KC -73 BFC 65 XFC-120 PC -120 SC 32 BSC 15 XSC =0; END 下面的模型是上面模型的集合版本： MODEL: SETS: COLD/BF1,BS1,BFC,BSC,XFC,XSC,PC,SC,KC/: QTY,FUEL,SALT,COST1,COST2,SALV,TRUCKVAL, PLOWVAL; ENDSETS DATA: c0sT1=70200000001; FUEL=-10-1010110: SALT=0-10-101010: TRUCKVAL 000000 11 0; PL0WVAL=00000011.10: C0ST2=00-73-326515-120-1201: ENDDATA MIN @SUM(COLD(I):QTY COST1); @SUM(COLD I):QTY FUEL)=0; @SUM(COLD(I):QTY SALT)=0; @SUM(COLD(I):TRUCKVAL QTY)=5100; @SUM(COLD(I):COST2 QTY)=0; END 这个模型的解答稍微复杂一点。在严冬季节，按假设铲雪的效率稍稍高于撒盐的效率。 这是因为：撒盐一天的费用为：120+32+73=225，和铲雪相比较的费用是：225/1.1=204.5： 而铲雪一天的费用：120+73=193。所以，在严冬，铲雪的效率大于撒盐的效率。 当然，由于“车天”数量的限制，一个“纯铲雪”的决策无法实现。因此，一定要使用 部分清雪车撒盐除雪，才能确保有充足的除雪能力。下面是相应的解答： Global optimal solution found at step: 4

8 KC - 73 * BFC + 65 * XFC - 120 * PC - 120 * SC - 32 * BSC + 15 * XSC = 0; END 下面的模型是上面模型的集合版本： MODEL: SETS: COLD/BF1, BS1, BFC, BSC, XFC, XSC, PC, SC, KC/: QTY, FUEL, SALT, COST1, COST2, SALV, TRUCKVAL, PLOWVAL; ENDSETS DATA: COST1 = 70 20 0 0 0 0 0 0 1; FUEL = -1 0 -1 0 1 0 1 1 0; SALT = 0 -1 0 -1 0 1 0 1 0; TRUCKVAL = 0 0 0 0 0 0 1 1 0; PLOWVAL = 0 0 0 0 0 0 1 1.1 0; COST2 = 0 0 -73 -32 65 15 -120 -120 1; ENDDATA MIN = @SUM( COLD( I): QTY * COST1); @SUM( COLD( I): QTY * FUEL) = 0; @SUM( COLD( I): QTY * SALT) = 0; @SUM( COLD( I): TRUCKVAL * QTY) = 5100; @SUM( COLD( I): COST2 * QTY) = 0; END 这个模型的解答稍微复杂一点。 在严冬季节，按假设铲雪的效率稍稍高于撒盐的效率。 这是因为：撒盐一天的费用为：120+32+73=225，和铲雪相比较的费用是：225/1.1=204.5； 而铲雪一天的费用：120+73=193。所以，在严冬，铲雪的效率大于撒盐的效率。 当然，由于“车天”数量的限制，一个“纯铲雪”的决策无法实现。因此，一定要使用 部分清雪车撒盐除雪，才能确保有充足的除雪能力。下面是相应的解答： Global optimal solution found at step: 4

9 Objective value: 970000.0 Variable Value Reduced Cost BF1 5000.000 0.0000000 BS1 1000.000 0.0000000 KC 600000.0 0.0000000 BFC 0.0000000 3.000000 XFC 0.0000000 5.000000 PC 4000.000 0.0000000 sc 1000.000 0.0000000 BSC 0.0000000 12.00000 XSC 0.0000000 5.000000 如果事先知道是严冬，答案就是：在第1期购买5000车天燃料和1000车天食盐，在第2期 用4000铲雪车天和1000撒盐车天”除雪，无须再购买任何燃料和食盐(BFC=BSC=0),而且到 了冬季结束的时候，燃料和食盐都没有剩余(XFC=XSC=O)。 7.4.3无条件解答 当然，上面两个模型或解答本身不能立即投入使用。这是由于它们都是在假设未来的气 候己知的情况下得到的。而未来的气候到底是什么我们并不知道。这里存在一个问题，就是 两个模型中关于第1期的决策并不相同。现实中，不论将来的天气是暖冬还是严冬，第1期 的决策都应该一样。当然，这也很容易处理。我们可以简单地将两个模型合并起来。由于第 1期的两个决策变量BF1和BS1同时出现两个模型的约束集合中，如果将模型合并起来，不 论将来的天气是暖冬还是严冬，第1期的决策变量必取唯一的值。 接下来，我们就要为合并起来的模型确定相应的目标函数。很显然，第1期的成本系 数是确定的。然而，第2期的成本变量KW和KC是随机变量。KW有意义而KC无意义（等 于0)具有0.4的概率：KC有意义而KW无意义（等于0）具有0.6的概率。所以，在目标 函数中，应该分别为KW和KC赋予0.4和0.6的权重。这样，就得到下面的无条件模型： MODEL: MIN=70*BF1+20*BS1+4*KW+.6*KC: -BF1 BFW XFW PW SW 0;

9 Objective value: 970000.0 Variable Value Reduced Cost BF1 5000.000 0.0000000 BS1 1000.000 0.0000000 KC 600000.0 0.0000000 BFC 0.0000000 3.000000 XFC 0.0000000 5.000000 PC 4000.000 0.0000000 SC 1000.000 0.0000000 BSC 0.0000000 12.00000 XSC 0.0000000 5.000000 如果事先知道是严冬，答案就是：在第1期购买5000车天燃料和1000车天食盐，在第2期 用4000铲雪车天和1000撒盐车天”除雪，无须再购买任何燃料和食盐(BFC=BSC=0)，而且到 了冬季结束的时候，燃料和食盐都没有剩余(XFC=XSC=0) 。 7.4.3 无条件解答 当然，上面两个模型或解答本身不能立即投入使用。这是由于它们都是在假设未来的气 候已知的情况下得到的。而未来的气候到底是什么我们并不知道。这里存在一个问题，就是 两个模型中关于第 1 期的决策并不相同。现实中，不论将来的天气是暖冬还是严冬，第 1 期 的决策都应该一样。当然，这也很容易处理。我们可以简单地将两个模型合并起来。由于第 1 期的两个决策变量 BF1 和 BS1 同时出现两个模型的约束集合中，如果将模型合并起来，不 论将来的天气是暖冬还是严冬，第 1 期的决策变量必取唯一的值。 接下来，我们就要为合并起来的模型确定相应的目标函数。很显然，第 1 期的成本系 数是确定的。然而，第 2 期的成本变量 KW 和 KC 是随机变量。KW 有意义而 KC 无意义（等 于 0）具有 0.4 的概率；KC 有意义而 KW 无意义（等于 0）具有 0.6 的概率。所以，在目标 函数中，应该分别为 KW 和 KC 赋予 0.4 和 0.6 的权重。这样，就得到下面的无条件模型： MODEL: MIN = 70 * BF1 + 20 * BS1 + .4 * KW + .6 * KC; -BF1 - BFW + XFW + PW + SW = 0;

10 -BS1 BSW XSW SW 0; PW+SW=3500: KW-73*BFW-30*BSW+65*XFW-110*PW-110*SW=0: -BF1 BFC XFC PC SC 0; -BS1 SC BSC XSC 0; PC+SC=5100; KC-73*.BFC+65*XFC-120*PC-120*SC-32*BSC+15*XSC =0； END 为了进一步理解这个模型，可以看看下面的模型系数图示： BB B X B X B X B X p FS F F H 1 W C C 70200.4 0.6 MIN 少 -1 -1 1 =0 3: -1 1 -1 =0 1 1 3500 6 1-7365-110-110305 =0 -1111 =0 1-1 1 11 1500 11: 1-7365-120-120-3215=0 无条件模型由两个子模型组成：一个是位于右下方的严冬模型：一个是位于左上方的暖 冬模型。这两个模型除了共有最左边的两个第1期的决策变量BF1和BS1以外，其余部分完 全独立。我们可以将这个无条件模型简单地描述如下： Minimize第1期成本+0.4（暖冬情况下第2期成本） +0.6(严冬情况下第2期成本)

10 -BS1 - BSW + XSW + SW = 0; PW + SW = 3500; KW - 73 * BFW - 30 * BSW + 65 * XFW - 110 * PW - 110 * SW=0; -BF1 - BFC + XFC + PC + SC = 0; -BS1 + SC - BSC + XSC = 0; PC + SC = 5100; KC - 73 * BFC + 65 * XFC - 120 * PC - 120 * SC - 32 * BSC + 15 * XSC = 0; END 为了进一步理解这个模型，可以看看下面的模型系数图示： B F 1 B S 1 K W B F W X F W P W S W B S W X S W K C B F C X F C P C S C B S C X S C R H S 1: 70 20 0.4 0.6 MIN 2: -1 -1 1 1 1 =0 3: -1 1 -1 1 =0 4: 1 1 3500 6: 1 -73 65 -110 -110 30 5 =0 7: -1 -1 1 1 1 =0 8: -1 1 -1 1 =0 9: 1 1 1500 11: 1 -73 65 -120 -120 -32 15 =0 无条件模型由两个子模型组成：一个是位于右下方的严冬模型；一个是位于左上方的暖 冬模型。这两个模型除了共有最左边的两个第 1 期的决策变量 BF1 和 BS1 以外，其余部分完 全独立。我们可以将这个无条件模型简单地描述如下： Minimize 第 1 期成本 + 0.4 (暖冬情况下第 2 期成本) + 0.6 (严冬情况下第 2 期成本)