安徽大学：《运筹学》课程理论教案（PPT讲稿）第八章 图与网络分析

第八章 图图与网络分析 图的基本概念 最小树问题 最短路问题 最大流问题 最小费用流问题 中国邮路问题 3

3 第八章 图与网络分析 图的基本概念 最小树问题 最短路问题 最大流问题 最小费用流问题 中国邮路问题

当我们在研究某些现实系统时，如果系统中 含有有限个待研究的对象，除了关心这些对象本 身的特性，同时还要考虑对象之间的相互关系 一个比较简单并且是常用的方法就是画一张图 用点表示系统中的对象，用点之间的连线表示对 象之间的相互关系。通过对图的研究，达到研究 系统的目的。例如我们经常见到的道路交通图 管道网络图、工程计划图等。用图来表达和研究 个系统往往具有直观、简洁和方便等特点。 4

4 引 言 当我们在研究某些现实系统时，如果系统中 含有有限个待研究的对象，除了关心这些对象本 身的特性，同时还要考虑对象之间的相互关系， 一个比较简单并且是常用的方法就是画一张图， 用点表示系统中的对象，用点之间的连线表示对 象之间的相互关系。通过对图的研究，达到研究 系统的目的。例如我们经常见到的道路交通图、 管道网络图、工程计划图等。用图来表达和研究 一个系统往往具有直观、简洁和方便等特点

引言 图论(Graph Theory)是运筹学的一个重要分 支，它是建立和处理离散数学模型的一个重要工 具。 图论的研究最早可追溯到著名的哥尼斯堡七 桥问题。18世纪欧洲的哥尼斯堡城有一条流经全 城的普雷格尔河，河的两岸和河中两个小岛有七 座桥彼此相通（如图8-1所示）。 5

5 引 言 图论(Graph Theory)是运筹学的一个重要分 支，它是建立和处理离散数学模型的一个重要工 具。 图论的研究最早可追溯到著名的哥尼斯堡七 桥问题。18世纪欧洲的哥尼斯堡城有一条流经全 城的普雷格尔河，河的两岸和河中两个小岛有七 座桥彼此相通(如图8-1所示)

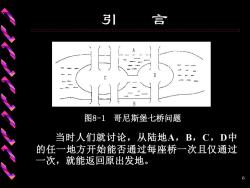
3引 言 、 图8-1 哥尼斯堡七桥问题 当时人们就讨论，从陆地A,B,C,D中 的任一地方开始能否通过每座桥一次且仅通过 一次，就能返回原出发地。 6

6 引 言 图8-1 哥尼斯堡七桥问题 当时人们就讨论，从陆地A，B，C，D中 的任一地方开始能否通过每座桥一次且仅通过 一次，就能返回原出发地

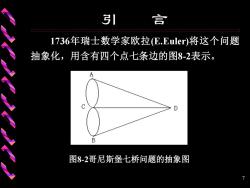
引 言 1736年瑞士数学家欧拉E.Euler)将这个问题 抽象化，用含有四个点七条边的图8-2表示。 B 图8-2哥尼斯堡七桥问题的抽象图 7

7 引 言 1736年瑞士数学家欧拉(E.Euler)将这个问题 抽象化，用含有四个点七条边的图8-2表示。 图8-2哥尼斯堡七桥问题的抽象图

引 言 探讨从图中任一点出发，是否能一笔画出图 8-2(即一笔画问题)，欧拉发表了第一篇关于图的 论文，证明了七桥问题不能实施一笔画，结束了 当时人们的争论。从而欧拉被公认为图论的奠基 人。 1852年F.格思里提出了著名的四色猜想问题 幅地图只要用四种不同颜色着色，就可以使互 相接壤的国家由不同的颜色来区分。1890年有人 证明了五色定理。四色问题直到1976年才由美国 学者Appel,.Haken等用电子计算机完成证明。 8

8 引 言 探讨从图中任一点出发，是否能一笔画出图 8-2(即一笔画问题)，欧拉发表了第一篇关于图的 论文，证明了七桥问题不能实施一笔画，结束了 当时人们的争论。从而欧拉被公认为图论的奠基 人。 1852年F.格思里提出了著名的四色猜想问题， 一幅地图只要用四种不同颜色着色，就可以使互 相接壤的国家由不同的颜色来区分。1890年有人 证明了五色定理。四色问题直到1976年才由美国 学者Appel，Haken等用电子计算机完成证明

引 言 1859年汉密尔顿提出：十二面体中的20个角 分别表示20个城市，从某城市出发，访遍所有城 市，且仅访问一次，返回出发地的Hamilton回路 问题。1936年哥尼格发表了第一本图论专著，从 此图论成为一门独立的学科。 目前图论与计算机科学、 系统论、控制论等 学科密切结合，在工程技术、 生物化学、系统工 程、通讯科学等领域得到广泛的应用 9

9 引 言 1859年汉密尔顿提出：十二面体中的20个角 分别表示20个城市，从某城市出发，访遍所有城 市，且仅访问一次，返回出发地的Hamilton回路 问题。1936年哥尼格发表了第一本图论专著，从 此图论成为一门独立的学科。 目前图论与计算机科学、系统论、控制论等 学科密切结合，在工程技术、生物化学、系统工 程、通讯科学等领域得到广泛的应用

3引 言 图论的方法同样可以应用到经济管理、辅助 决策等领域，图论已经成为运筹学的一个重要组 成部分，它是建立和处理离散型数学模型的一个 重要工具。本章将先简单介绍一些图的基本概念， 然后讨论图论中有关网络分析的一些典型问题 最短路问题，最小树问题，最大流问题、最小费 用流问题和中国邮递员问题。 10

10 引 言 图论的方法同样可以应用到经济管理、辅助 决策等领域，图论已经成为运筹学的一个重要组 成部分，它是建立和处理离散型数学模型的一个 重要工具。本章将先简单介绍一些图的基本概念， 然后讨论图论中有关网络分析的一些典型问题： 最短路问题，最小树问题，最大流问题、最小费 用流问题和中国邮递员问题

第一节图的基本概念 图 在实际问题中，人们经常用“图”来表示所 研究的对象以及这些对象相互之间某种特定关系。 例如在图8-3中，我们用图表示了A,B,C, D,E五个城镇相对位置以及连接它们的公路网。 A E C 图8-3城镇公路网 11

11 第一节 图的基本概念 一、图 在实际问题中，人们经常用“图”来表示所 研 究的对象以及这些对象相互之间某种特定关系。 例如在图8-3中，我们用图表示了A，B，C， D，E五个城镇相对位置以及连接它们的公路网。 图8-3 城镇公路网

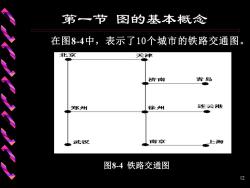
第一节图的基本概念 在图8-4中，表示了10个城市的铁路交通图。 北京 天津 济南 青岛 关郑州 徐州 连云港 武汉 南京 上海 图8-4铁路交通图 12

12 第一节 图的基本概念 在图8-4中，表示了10个城市的铁路交通图。 图8-4 铁路交通图