安徽大学：《运筹学》课程实验教案（PPT讲稿）第三讲 分析解答

第三讲 利用LNGO求解数学规划 解答报考的经济分析 对偶价格和递减成本的关系 对偶价格和递减成本的变化范围 约束系数的敏感性分析 对偶LP问题，房东与租赁者 3

3 第三讲 利用LINGO 求解数学规划 解答报考的经济分析 对偶价格和递减成本的关系 对偶价格和递减成本的变化范围 约束系数的敏感性分析 对偶LP问题，房东与租赁者

3.1解答报告的经济分析 3.1解答报告的经济分析 我们可以从一个模型的解答报告中收集到很 多有趣的经济信息。另外，从最优报告中（例如 敏感性分析)还可以收集到更多的其它信息。我 们利用这些信息就可以做出一个快速的“watf 分析。典型的“what if"'问题是： (a)如果改变产量或需求量，结果会怎样？ (b)如果有了一个新的机会，它是否可行？ 是否值得去利用？ 4

4 3.1 解答报告的经济分析 3.1 解答报告的经济分析 我们可以从一个模型的解答报告中收集到很 多有趣的经济信息。另外，从最优报告中（例如 敏感性分析）还可以收集到更多的其它信息。我 们利用这些信息就可以做出一个快速的“what if” 分析。典型的“what if”问题是： （a）如果改变产量或需求量，结果会怎样？ （b）如果有了一个新的机会，它是否可行？ 是否值得去利用？

3.2对偶价格和递减成本之间的经济关系 3.2对偶价格和递减成本之间的经济关系 读者或许认为：“递减成本就是对偶价格 定是谬论。按照我们的约定， 变量X的递减成 本就是该变量对应的约束X≥0的对偶价格。回忆 前面，变量X的递减成本表示变量X从0增加一个 单位时，目标函数值恶化的数量；约束X≥0的对 偶价格表示约束右边的常数从0增加一个单位时， 目标函数值改进的数量 5

5 3.2对偶价格和递减成本之间的经济关系 3.2 对偶价格和递减成本之间的经济关系 读者或许认为：“递减成本就是对偶价格” 一定是谬论。按照我们的约定，变量X的递减成 本就是该变量对应的约束X≥0的对偶价格。回忆 前面，变量X的递减成本表示变量X从0增加一个 单位时，目标函数值恶化的数量；约束X≥0的对 偶价格表示约束右边的常数从0增加一个单位时， 目标函数值改进的数量

3.2对偶价格和递减成本之间的经济关系 下面我们将进一步解释递减成本，并讨论递 减成与对偶价格之间的关系。事实上，如果我们 用活动占用资源的对偶价格来估算活动的成本， 那么，这里的递减成本就是一种净成本。这听起 来似乎有点经济味道。如果强行让一个未被使用 的活动增加一个单位，那么这必将占用一定的资 源。而这些资源都有对偶价格。所以，我们就可 以用活动相关的对偶价格来估计活动的成本。让 我们来看一个例子，检验一下这个结论是否正确

6 3.2对偶价格和递减成本之间的经济关系 下面我们将进一步解释递减成本，并讨论递 减成与对偶价格之间的关系。事实上，如果我们 用活动占用资源的对偶价格来估算活动的成本， 那么，这里的递减成本就是一种净成本。这听起 来似乎有点经济味道。如果强行让一个未被使用 的活动增加一个单位，那么这必将占用一定的资 源。而这些资源都有对偶价格。所以，我们就可 以用活动相关的对偶价格来估计活动的成本。让 我们来看一个例子，检验一下这个结论是否正确

3.2对偶价格和递减成本之间的经济关系 3.2.1关于成本估算的一个说明 假设Enginola公司正在考虑一个录像机产品 的投产问题。市场研究表明：生产一台录像机可 获直接利润$47。录像机可以由Asto生产线制造 而且每台需要3小时的劳动力。如果该录像机投产 它必将减少Asr0的产量（因为它们使用同一个生 产线)，也可能减少Cosmo的产量（因为总劳动 力是有限的)。那么， 录像机产品是否值得投产 呢？从表面上看，还是有希望的 7

7 3.2对偶价格和递减成本之间的经济关系 3.2.1 关于成本估算的一个说明 假设Enginola公司正在考虑一个录像机产品 的投产问题。市场研究表明：生产一台录像机可 获直接利润$47。录像机可以由Astro生产线制造， 而且每台需要3小时的劳动力。如果该录像机投产， 它必将减少Astro的产量（因为它们使用同一个生 产线），也可能减少Cosmo的产量（因为总劳动 力是有限的）。那么，录像机产品是否值得投产 呢？从表面上看，还是有希望的

3.2对偶价格和递减成本之间的经济关系 与Coso相比，录像机单位劳动小时的利润 要大一些；与Asr0相比，录像机单位产品的利润 要大一些。回忆一下原问题解答中，Asr0生产能 力的对偶价格是$5，劳动力的对偶价格是$15。如 果我们将这个变量加入到模型中，目标函数中的 系数多了+47，第2行(As0生产能力约束)中的 系数多了+1，第4行（劳动力约束）中的系数多 了+3。我们可以用一个活动（或决策变量）占用 的资源来估计它的成本 8

8 3.2对偶价格和递减成本之间的经济关系 与Cosmo相比，录像机单位劳动小时的利润 要大一些；与Astro相比，录像机单位产品的利润 要大一些。回忆一下原问题解答中，Astro生产能 力的对偶价格是$5，劳动力的对偶价格是$15。如 果我们将这个变量加入到模型中，目标函数中的 系数多了+47，第2行（Astro生产能力约束）中的 系数多了+1，第4行（劳动力约束）中的系数多 了+3。我们可以用一个活动（或决策变量）占用 的资源来估计它的成本

3.2对偶价格和递减成本之间的经济关系 那么用什么价格来估计呢？显而易见，应该 用对偶价格。+47的利润可以认为是具有-47的成 本。可以用下面的表格来进行成本的计算 Mode1 MAX=20*A+30*C+47*V; A V<=60; <= 50； A+2*C+3*V<=120;End 9

9 3.2对偶价格和递减成本之间的经济关系 那么用什么价格来估计呢？显而易见，应该 用对偶价格。+47的利润可以认为是具有-47的成 本。可以用下面的表格来进行成本的计算： Model MAX = 20*A+30*C+47*V; A + V <= 60; C <= 50; A + 2*C + 3*V <= 120; End

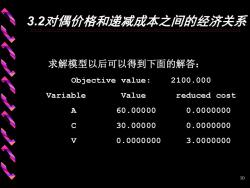
3.2对偶价格和递减成本之间的经济关系 求解模型以后可以得到下面的解答 Objective value: 2100.000 Variable Value reduced cost A 60.00000 0.0000000 30.00000 0.0000000 0.0000000 3.0000000 10

10 3.2对偶价格和递减成本之间的经济关系 求解模型以后可以得到下面的解答： Objective value: 2100.000 Variable Value reduced cost A 60.00000 0.0000000 C 30.00000 0.0000000 V 0.0000000 3.0000000

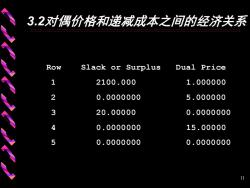
3.2对偶价格和递减成本之间的经济关系 Slack or Surplus Dual Price 1 2100.000 1.000000 2 0.0000000 5.000000 3 20.00000 0.0000000 4 0.0000000 15.00000 5 0.0000000 0.0000000 11

11 3.2对偶价格和递减成本之间的经济关系 Row Slack or Surplus Dual Price 1 2100.000 1.000000 2 0.0000000 5.000000 3 20.00000 0.0000000 4 0.0000000 15.00000 5 0.0000000 0.0000000

3.2对偶价格和递减成本之间的经济关系 录像机的产量为0。注意：V的递减成本是S3, 与我们前面的计算结果一样。这个例子就是下面 结论的一个很好的说明 个活动的机会成本等于使用资源的加权和 减去它的利润加权总和。这里的权数就是对偶价 格。对于一个最小化问题，目标函数的对偶价格 为+1；对于一个最大化问题，目标函数的对偶价 格为1。 12

12 3.2对偶价格和递减成本之间的经济关系 录像机的产量为0。注意：V的递减成本是$3， 与我们前面的计算结果一样。这个例子就是下面 结论的一个很好的说明： 一个活动的机会成本等于使用资源的加权和 减去它的利润加权总和。这里的权数就是对偶价 格。对于一个最小化问题，目标函数的对偶价格 为+1；对于一个最大化问题，目标函数的对偶价 格为-1