《数字电子技术》课程教学课件（PPT讲稿）第一章 逻辑代数基础与EDA技术的基础知识 CH12 逻辑函数的化简方法

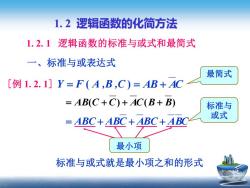
1.2逻辑函数的化简方法 1.2.1逻辑函数的标准与或式和最简式 一、标准与或表达式 最简式 1.2.1]Y=F(A,B,C)=AB+AC =AB(C+C)+AC(B+B) 标准与 =ABC+ABC+ABC+ABC∠ 或式 最小项 标准与或式就是最小项之和的形式

一、标准与或表达式 Y = F ( A ,B ,C ) = ABC + ABC + ABC + ABC = AB + AC 1. 2 逻辑函数的化简方法 1. 2. 1 逻辑函数的标准与或式和最简式 = AB(C + C) + AC(B + B) 标准与 或式 标准与或式就是最小项之和的形式 最小项 最简式 [例 1. 2. 1]

1.最小项的概念： 包括所有变量的乘积项，每个变量均以原变量或 反变量的形式出现一次。 Y=F(A,B） (2变量共有4个最小项) AB AB AB AB Y=F(A,B,C) （3变量共有8个最小项) ABC ABCABC ABC ABC ABC ABC ABC Y=F(A,B,C,D)（4变量共有16个最小项) ABCD ABCD ABCD .ABCD ABCD (n变量共有2"个最小项)

1. 最小项的概念： 包括所有变量的乘积项，每个变量均以原变量或 反变量的形式出现一次。 Y = F ( A ,B ) ( 2 变量共有 4 个最小项) AB AB AB AB Y = F(A ,B ,C ,D) ( 4 变量共有 16 个最小项) ( n 变量共有 2 n个最小项) ABCD ABCD ABCD . . ABCD ABCD Y = F ( A ,B ,C ) ( 3 变量共有 8 个最小项) ABC ABC ABC ABC ABC ABC ABC ABC

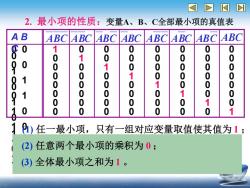
2.最小项的性质：变量A、B、C全部最小项的真值表 ABC ABC ABC ABC ABC ABC ABC ABC 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 00 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 00 0 0 0 0 0 0 0 0 任一最小项，只有一组对应变量取值使其值为1； (2)任意两个最小项的乘积为0； 3)全体最小项之和为1

ABC = 1 ABC = 1 对应规律：1  原变量 0  反变量 2. 最小项的性质： 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 A B C ABC ABC ABC ABC ABC ABC ABC ABC (1) 任一最小项，只有一组对应变量取值使其值为 1 ； A B C 0 0 1 A B C 1 0 1 (2) 任意两个最小项的乘积为 0 ； (3) 全体最小项之和为 1 。 变量A、B、C全部最小项的真值表

3.最小项是组成逻辑函数的基本单元 任何逻辑函数都是由其变量的若干个最小项构成， 都可以表示成为最小项之和的形式。 [例1.2.2]写出下列函数的标准与或式： Y=F(A,B,C)=AB+BC+CA []Y=AB(C+C)+BC(A+A)+CA(B+B) =ABC+ABC+ABC+ABC+ABC+ABC =ABC+ABC+ABC+ABC 相同最小 项合并 标准与或表达式是唯一的，一个函数只有 最小项之和的表达式

3. 最小项是组成逻辑函数的基本单元 Y = F( A ,B ,C ) = AB+ BC +CA = ABC + ABC+ ABC + ABC+ ABC + ABC 任何逻辑函数都是由其变量的若干个最小项构成， 都可以表示成为最小项之和的形式。 Y = AB(C + C) + BC(A+ A) + CA(B + B) [例 1. 2. 2] 写出下列函数的标准与或式： [解] 相同最小 项合并 = ABC + ABC + ABC + ABC 标准与或表达式是唯一的，一个函数只有一个 最小项之和的表达式

函数的标准与或式也可以由其真值表直接写出： 例如，已知Y=A+BC的真值表 B A+BC 函数的标准与或式 0 0 0 Y=(A+B)(A+C) 0 0 0 0 =ABC+ABC+ABC+ABC 0 0 0 0 0

函数的标准与或式也可以由其真值表直接写出： 例如，已知 Y = A + BC 的真值表 A B C A+ BC 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 0 1 1 1 1 1 = ABC + ABC + ABC + ABC 函数的标准与或式 Y = (A+ B)(A+ C)

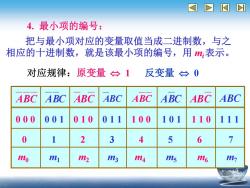
I 4.最小项的编号： 把与最小项对应的变量取值当成二进制数，与之 相应的十进制数，就是该最小项的编号，用m:表示。 对应规律：原变量台1 反变量台0 ABC ABC ABC ABC ABC ABC ABC ABC 000 001 010 011 100 101 110 111 0 1 2 3 4 5 6 o mi m2 3 ms ms m6 m

4. 最小项的编号： 把与最小项对应的变量取值当成二进制数，与之 相应的十进制数，就是该最小项的编号，用 mi 表示。 对应规律：原变量  1 反变量  0 ABC ABC ABC ABC ABC ABC ABC ABC 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 1 2 3 4 5 6 7 m0 m1 m2 m3 m4 m5 m6 m7

[例]写出下列函数的标准与或式： Y=AB+AD+BC=(A+B)(A+D)(B+C) =(A+BD)(B+C)=AB+AC+BCD =AB(C+C)+AC(B+B)+BCD(A+A) =ABC+ABC+ABC+ABC D+ABC D -ABCD+ABCD+ABCD+ABC D 与前面m m m6 ms ms 相重 +ABCD+ABCD+ABCD m mo ms =m +m+ms +m+m+mo+ms =∑m(0,1,4,5,6,7,8)

[例] 写出下列函数的标准与或式： Y = AB+ AD + BC = (A+ B) (A+ D) (B + C) = (A+ B D) (B + C) = AB+ AC + BC D = AB(C + C) + AC(B + B) + B C D(A+ A) = ABC + ABC + ABC + ABC D+ ABC D A B CD A B C D AB C D A B C D ABCD AB C D ABCD ABC D + + + + = + + + m7 m6 m5 m4 m1 m0 m8 = m7 +m6 +m5 + m4 + m1 + m0 + m8 =  ( 0 , 1, 4 , 5 , 6 , 7 , 8 ) m m0 与前面m0 相重

二、逻辑函数的最简表达式 1.最简与或式：乘积项的个数最少，每个乘积项中相 乘的变量个数也最少的与或表达式。 例如：Y=AB+AC+BC+BCD =AB+AC+BC=AB+AC 2.最简与非- 非号最少，每个非号下面相乘的变量 与非式： 个数也最少的与非-与非式。 [例1.2.3]写出下列函数的最简与非-与非式： Y=AB+AC [解]Y=AB+AC=AB·AC

二、逻辑函数的最简表达式 Y = AB+ AC + BC + BCD 1. 最简与或式： 乘积项的个数最少，每个乘积项中相 乘的变量个数也最少的与或表达式。 例如： = AB+ AC + BC = AB+ AC 2. 最简与非 – 与非式： 非号最少，每个非号下面相乘的变量 个数也最少的与非 - 与非式。 [例 1. 2. 3] 写出下列函数的最简与非 - 与非式： Y = AB+ AC [解] Y = AB+ AC = AB AC

ID☑I 3.最简或与式：括号个数最少，每个括号中相加的变 量的个数也最少的或与式。 [例1.2.4]写出下列函数的最简与或式： Y=AB+AC [解]Y=AB+AC Y=AB+AC AB.AC =(A+B)(A+C) 4.最简或非一非号个数最少，非号下面相加的变量 或非式： 个数也最少的或非-或非式。 [例1.2.5] 写出下列函数的最简或非一或非式： Y=AB+AC [解] Y=(A+B)(A+C) =A+B+A+(

= (A+ B) (A+ C) 3. 最简或与式： 括号个数最少，每个括号中相加的变 量的个数也最少的或与式。 [例 1. 2. 4] 写出下列函数的最简与或式： Y = AB+ AC [解] Y = AB+ AC Y = AB + AC = AB AC 4. 最简或非 – 或非式： 非号个数最少，非号下面相加的变量 个数也最少的或非 – 或非式。 [例 1. 2. 5] 写出下列函数的最简或非 – 或非式： Y = AB+ AC [解] Y = (A+ B) (A+ C) = A+ B + A+ C

✉D冈I 5.最简与或非式：非号下面相加的乘积项的个数最少， 每个乘积项中相乘的变量个数也最 少的与或非式。 [例1.2.6]写出下列函数的最简与或非式： Y=AB+AC [解]已知Y=A+B+A+C=AB+AC 结论： 只要得到函数的最简与或式，再用摩根定 理进行适当变换，就可以获得其它几种类 型的最简式。而最简与或式一般需要经过 化简才能求得

5. 最简与或非式： 非号下面相加的乘积项的个数最少， 每个乘积项中相乘的变量个数也最 少的与或非式。 [例 1. 2. 6] 写出下列函数的最简与或非式： Y = AB+ AC [解] Y = A+ B + A+ C = AB + AC 结论： 只要得到函数的最简与或式，再用摩根定 理进行适当变换，就可以获得其它几种类 型的最简式。而最简与或式一般需要经过 化简才能求得。 已知