《数字电子技术》课程授课教案（讲义）第5章 时序逻辑电路

第5章时序逻辑电路 【本章知识架构】 时序逻辑电路 结构特点 的特点、分类 分类 时序逻辑电路 分析步骤 多 的分析方法 序 分析举例 色 同先时序罗据 设计步骤 辑 异步计数器 电路设计万法 电 设计举例 同步计数器 路 常用时序逻辑 计数器 集成计数器及应用 功能器件 寄存器 基本寄存器 顺序脉冲 时序罗辑电路 移位寄存器及应用 发生器 的案例引入 案例分析 【本章教学目标与要求】 ·熟悉时序逻辑电路在电路结构和逻辑功能上的特点、分类 ·了解时序逻辑电路逻辑功能的表示方法 ·掌握时序逻辑电路的分析方法和同步时序逻辑电路设计方法 ·熟悉计数器、寄存器、顺序脉冲发生器的功能、应用 ·掌握常用集成时序逻辑器件的逻辑功能及使用方法 ·掌握反馈归零、置数法构成N进制计数器

第 5 章 时序逻辑电路 【本章知识架构】 【本章教学目标与要求】 ·熟悉时序逻辑电路在电路结构和逻辑功能上的特点、分类 ·了解时序逻辑电路逻辑功能的表示方法 ·掌握时序逻辑电路的分析方法和同步时序逻辑电路设计方法 ·熟悉计数器、寄存器、顺序脉冲发生器的功能、应用 ·掌握常用集成时序逻辑器件的逻辑功能及使用方法 ·掌握反馈归零、置数法构成 N 进制计数器 时 序 逻 辑 电 路 时序逻辑电路 的特点、分类 时序逻辑电路 的分析方法 同步时序逻辑 电路设计方法 常用时序逻辑 功能器件 结构特点 分类 分析步骤 分析举例 设计步骤 设计举例 计数器 寄存器 时序逻辑电路 的案例引入 案例分析 异步计数器 同步计数器 集成计数器及应用 顺序脉冲 发生器 基本寄存器 移位寄存器及应用

5.1概述 5.1.1时序逻辑电路的结构特点 时序逻辑电路：电路任何一时刻的输出状态不仅与该时刻的输入信号有关，而且 还与电路的原状态有关。时序电路中含有具有记忆能力的存储器件（最常用的是触发 器)和反馈通道。 JK触发器就是一个最简单的时序电路。 例如：JK触发器，其特征方程：Q1=JQ+KQ。Q1和当前的输入人、K有关， 还与过去的Q有关。 由触发器作存储器件的时序电路的结构框图如图51所示，一般来说，它由组合 电路和触发器两部分组成。 输入五 Z1输出 信号 组合电路 信号 触发器 触发器 输出信号 电路 -CP 图51时序逻辑电路框图 5.1.2时序逻辑电路的分类 按照电路状态变化的特点，时序电路分为同步时序电路和异步时序电路两大类。 同步时序电路内部触发器的状态更新在时钟脉冲作用下是同时进行的，即电路中 有一个统一的时钟脉冲，每来一个时钟脉冲，电路的状态只改变一次。 异步时序电路各个触发器的时钟脉冲不同，即电路中没有统一的时钟脉冲来控制 电路状态的变化，电路状态改变时，电路中要更新状态的触发器的翻转有先有后，是 异步进行的。 按照电路中输出变量是否和输入变量直接相关，时序电路又分为米里(Mey)型 电路和摩尔(Moore)型电路。 米里型电路的外部输出Z既与触发器的状态Q”有关，又与外部输入X有关。而

5.1 概 述 5.1.1 时序逻辑电路的结构特点 时序逻辑电路：电路任何一时刻的输出状态不仅与该时刻的输入信号有关，而且 还与电路的原状态有关。时序电路中含有具有记忆能力的存储器件（最常用的是触发 器）和反馈通道。 JK 触发器就是一个最简单的时序电路。 例如：JK 触发器，其特征方程： n n n 1 Q JQ KQ + = + 。 n 1 Q + 和当前的输入 J、K 有关， 还与过去的 n Q 有关。 由触发器作存储器件的时序电路的结构框图如图 5-1 所示，一般来说，它由组合 电路和触发器两部分组成。 图 5-1 时序逻辑电路框图 5.1.2 时序逻辑电路的分类 按照电路状态变化的特点，时序电路分为同步时序电路和异步时序电路两大类。 同步时序电路内部触发器的状态更新在时钟脉冲作用下是同时进行的，即电路中 有一个统一的时钟脉冲，每来一个时钟脉冲，电路的状态只改变一次。 异步时序电路各个触发器的时钟脉冲不同，即电路中没有统一的时钟脉冲来控制 电路状态的变化，电路状态改变时，电路中要更新状态的触发器的翻转有先有后，是 异步进行的。 按照电路中输出变量是否和输入变量直接相关，时序电路又分为米里（Mealy）型 电路和摩尔（Moore）型电路。 米里型电路的外部输出 Z 既与触发器的状态 n Q 有关，又与外部输入 X 有关。而

摩尔型电路的外部输出Z仅与触发器的状态Q”有关，而与外部输入X无关。 5.1.3时序电路逻辑功能的表示方法 时序电路的逻辑功能可用逻辑表达式、状态表、卡诺图、状态图、时序图和逻辑 图等六种方式表示，这些表示方法在本质上是相同的，可以互相转换。 5.2时序电路的分析和设计方法 5.2.1时序电路的分析方法 1.时序电路的一般分析步骤 (1)根据给定的时序电路图写出下列各逻辑方程式： 时钟方程。各触发器时钟端的逻辑表达式（对于同步时序电路这一步可省略）。 输出方程。时序电路的输出逻辑表达式，通常为现态和输入变量的函数。 驱动方程。各触发器输入端的逻辑表达式。 (2)将驱动方程代入相应触发器的特性方程，求得各触发器的次态方程，也就是 时序电路的状态方程。 (3)根据状态方程和输出方程，列出该时序电路的状态表，画出状态图或时序图。 (4)根据电路的状态表或状态图说明给定时序电路的逻辑功能。 2。同步时序电路的分析举例 【例5-1】试分析图53所示的时序电路 Q o.& 图53【例51】逻辑电路图 解：由于图53为同步时序电路，图中的三个触发器都接至同一个时钟脉冲源CP, 所以各触发器的时钟方程可以不写。该电路为Moor心型同步时序电路。 (1)写出输出方程：Z=Q”·Q (5-1)

摩尔型电路的外部输出 Z 仅与触发器的状态 n Q 有关，而与外部输入 X 无关。 5.1.3 时序电路逻辑功能的表示方法 时序电路的逻辑功能可用逻辑表达式、状态表、卡诺图、状态图、时序图和逻辑 图等六种方式表示，这些表示方法在本质上是相同的，可以互相转换。 5.2 时序电路的分析和设计方法 5.2.1 时序电路的分析方法 1．时序电路的一般分析步骤 （1）根据给定的时序电路图写出下列各逻辑方程式： 时钟方程。各触发器时钟端的逻辑表达式（对于同步时序电路这一步可省略）。 输出方程。时序电路的输出逻辑表达式，通常为现态和输入变量的函数。 驱动方程。各触发器输入端的逻辑表达式。 （2）将驱动方程代入相应触发器的特性方程，求得各触发器的次态方程，也就是 时序电路的状态方程。 （3）根据状态方程和输出方程，列出该时序电路的状态表，画出状态图或时序图。 （4）根据电路的状态表或状态图说明给定时序电路的逻辑功能。 2．同步时序电路的分析举例 【例 5-1】试分析图 5-3 所示的时序电路 图 5-3 【例 5-1】逻辑电路图 解：由于图 5-3 为同步时序电路，图中的三个触发器都接至同一个时钟脉冲源 CP， 所以各触发器的时钟方程可以不写。该电路为 Moore 型同步时序电路。 （1）写出输出方程： 1 2 n n Z Q Q =  （5-1）

(2)写出驱动方程： Jo=oro: =0: [52=0Q(5-2) K=1 K=010: K:=0" (3)写出JK触发器的特性方程Q=JQ+KQ,然后将各驱动方程代入JK 触发器的特性方程，得各触发器的次态方程： o=Joo:+Koo:=0foro: o"M=Jo"+K.o"=o"o"+o"o"o" (5-3) O=J2O:+Ko =OrO"O;+0"O" (4)作状态转换表及状态图 设触发器的初始状态QQ”Q=000,代入式(5-1)和(5-3)，得到新的一组状态和 输出，再将这组状态作为触发器的现态，分析下一个时钟脉冲到来后时序电路的次态 和输出，依次可以得到表5-1所示的状态转换表。 表5-1 现态 次 态 输出 oo o; 0:"Q""Q" Z 00 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 完整的状态转换图如图5-4所示。 000 /0 0 +001 /0 -(011 110 101 /0 0 (100 图5-4【例6-1】状态转换图 (5)画时序图

（2）写出驱动方程： 0 1 2 0 1 n n J Q Q K  =   = 0 0 2 1 1 n n n J Q K Q Q  =    = 0 1 1 2 2 n n n J Q Q K Q  =   = （5-2） （3）写出 JK 触发器的特性方程 n n n 1 Q JQ KQ + = + ，然后将各驱动方程代入 JK 触发器的特性方程，得各触发器的次态方程： 0 0 2 1 0 1 1 0 1 0 2 1 2 2 0 1 2 1 2 1 0 0 0 1 1 1 1 1 2 2 2 n n n n n n n n n n n n n n n n n n n n n n Q J Q K Q Q Q Q Q J Q K Q Q Q Q Q Q Q J Q K Q Q Q Q Q Q + + +  = + =    = + = +   = + = +  (5-3) （4）作状态转换表及状态图 设触发器的初始状态 2 1 0 000 nnn QQQ = ，代入式(5-1)和(5-3)，得到新的一组状态和 输出，再将这组状态作为触发器的现态，分析下一个时钟脉冲到来后时序电路的次态 和输出，依次可以得到表 5-1 所示的状态转换表。 表 5-1 现 态 次 态 输 出 2 n Q 1 n Q 0 n Q 1 2 n Q + 1 1 n Q + 1 0 n Q + Z 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 1 1 0 0 1 1 1 0 0 0 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 0 0 0 0 1 完整的状态转换图如图 5-4 所示。 图 5-4 【例 5-1】状态转换图 （5）画时序图

如图5-5所示。 CP 9 图5-5【例5-1】时序图 (6)逻辑功能分析 从状态转换表和状态转换图可以看出，当触发器的状态为Q226=110,下 个时钟脉冲到来后电路的次态QQQ=000,电路回到了设定的初始状态。 因此，在以后的时钟脉冲作用下，逻辑电路的状态和输出必然按表51所示的顺序反 复循环。每次状态到达110时，输出Z=1,故该电路是一个同步七进制计数器，输出 Z为计数器的进位信号。 三个触发器共有八种状态取值，七进制计数器只使用其中七种状态构成有效循 环，其中状态111没有用到，称为无效状态。将QQ=111作为初始状态代入式 (5-3)中，求得其次态Q+QQ1=000,其次态为有效循环状态 【例5-2】试分析图56所示的时序逻辑电路 图5-6【例5-2】逻辑电路图 解：由于图56为同步时序电路，图中的两个触发器都接至同一个时钟脉冲源CP, 所以各触发器的时钟方程可以不写。该电路为Mealy型同步时序逻辑电路。 (1)写出输出方程：Z=(X⊕Q")Q (5.4)

如图 5-5 所示。 图 5-5 【例 5-1】时序图 （6）逻辑功能分析 从状态转换表和状态转换图可以看出，当触发器的状态为 2 1 0 110 nnn QQQ = ，下一 个时钟脉冲到来后电路的次态 111 2 1 0 000 nnn QQQ +++ = ，电路回到了设定的初始状态。 因此，在以后的时钟脉冲作用下，逻辑电路的状态和输出必然按表 5-1 所示的顺序反 复循环。每次状态到达 110 时，输出 Z=1，故该电路是一个同步七进制计数器，输出 Z 为计数器的进位信号。 三个触发器共有八种状态取值，七进制计数器只使用其中七种状态构成有效循 环，其中状态 111 没有用到，称为无效状态。将 2 1 0 111 nnn QQQ = 作为初始状态代入式 (5-3)中，求得其次态 111 2 1 0 000 nnn QQQ +++ = ，其次态为有效循环状态。 【例 5-2】试分析图 5-6 所示的时序逻辑电路 图 5-6 【例 5-2】逻辑电路图 解：由于图 5-6 为同步时序电路，图中的两个触发器都接至同一个时钟脉冲源 CP， 所以各触发器的时钟方程可以不写。该电路为 Mealy 型同步时序逻辑电路。 （1）写出输出方程： n n Z X Q1 Q0 = (  )  （5-4）

(2)写出驱动方程： J=X⊕g (5-5a) K=1 J=X⊕06 (5-5b) K=1 (3)写出JK触发器的特性方程Q=Jg+,然后将各驱动方程代入JK触 发器的特性方程，得各触发器的次态方程： Q。=JQ6+KQ6=(X⊕g)g6 (5-6a) Q=J,2"+Kg=(X⊕Q)-g (5-6b (4)作状态转换表及状态图 由于输入控制信号X可取1，也可取0，所以分两种情况列状态转换表和画状态 图。 ①当X0时。 将-0代入输出方程(5-4)和触发器的次态方程(5-6)，则输出方程简化为： Z=gg:触发器的次态方程简化为：Q,”-gQ，g=Qgg(5-7) 设电路的现态为Q?=00,依次代入上述触发器的次态方程和输出方程中进行计 算，得到电路的状态转换表如表5-2所示。 根据表5-2所示的状态转换表可得状态转换图如图5-7所示。 (eP 表5-2X0时的状态表 现态 次态 输出 四”0”0 g1Q6 0 0 图570时的状态图 0 ②当=1时。 10 输出方程简化为：Z=Q: 0 0 触发器的次态方程简化为： Q。=grg,g=gg (5-8) 计算可得电路的状态转换表如表5-3所示，状态图如图5-8所示

（2）写出驱动方程： 0 1 0 1 n J X Q K  =    = （5-5 a） 1 0 1 1 n J X Q K  =    = （5-5b） （3）写出 JK 触发器的特性方程 n n n Q = JQ + KQ +1 ，然后将各驱动方程代入 JK 触 发器的特性方程，得各触发器的次态方程： n n n n n Q J 0 Q0 K0Q0 X Q1 Q0 1 0 = + = (  ) + （5-6a） n n n n n Q J1Q1 K1Q1 X Q0 Q1 1 1 = + = (  ) + （5-6b） （4）作状态转换表及状态图 由于输入控制信号 X 可取 1，也可取 0，所以分两种情况列状态转换表和画状态 图。 ①当 X=0 时。 将 X=0 代入输出方程（5-4）和触发器的次态方程（5-6），则输出方程简化为： n n Z = Q1 Q0 ；触发器的次态方程简化为： n n n Q Q1 Q0 1 0 = + ， n n n Q Q0 Q1 1 1 = + （5-7） 设电路的现态为 1 0 = 00 n n Q Q ，依次代入上述触发器的次态方程和输出方程中进行计 算，得到电路的状态转换表如表 5-2 所示。 根据表 5-2 所示的状态转换表可得状态转换图如图 5-7 所示。 ②当 X=1 时。 输出方程简化为： n n Z = Q1 Q0 ； 触发器的次态方程简化为： n n n Q Q1 Q0 1 0 = + ， n n n Q Q0 Q1 1 1 = + （5-8） 计算可得电路的状态转换表如表 5-3 所示，状态图如图 5-8 所示。 表 5-2 X=0 时的状态表 现 态 次态 输出 n Q1 n Q0 1 1 n+ Q 1 0 n+ Q Z 0 0 0 1 0 0 1 1 0 0 1 0 0 0 1 图 5-7 X=0 时的状态图

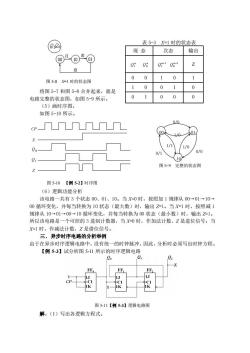
( 表5-3=1时的状态表 现态 次态 输出 @4⑩”@ 0 00 10 1 图581时的状态图 将图5-7和图5-8合并起来，就是 10 0 0 电路完整的状态图，如图59所示。 0 1 0 0 0 (5)画时序图， 如图5-10所示。 冂Π 1/八 1/0 21 10 图59完整的状态图 图5-10【例52】时序图 (6)逻辑功能分析 该电路一共有3个状态00、01、10。当X=0时，按照加1规律从00一01一10 00循环变化，并每当转换为10状态（最大数）时，输出Z=1。当=1时，按照减1 规律从10一01→00一10循环变化，并每当转换为00状态（最小数）时，输出2=1。 所以该电路是一个可控的3进制计数器，当X0时，作加法计数，Z是进位信号：当 X1时，作减法计数，Z是借位信号。 三。异步时序电路的分析举例 由于在异步时序逻辑电路中，没有统一的时钟脉冲，因此，分析时必须写出时钟方程。 【例5-3】试分析图5-11所示的时序逻辑电路 图5-11【例5-3】逻辑电路图 解：(1)写出各逻辑方程式

将图 5-7 和图 5-8 合并起来，就是 电路完整的状态图，如图 5-9 所示。 （5）画时序图。 如图 5-10 所示。 Q1 Q0 X CP Z 图 5-10 【例 5-2】时序图 （6）逻辑功能分析 该电路一共有 3 个状态 00、01、10。当 X=0 时，按照加 1 规律从 00→01→10→ 00 循环变化，并每当转换为 10 状态（最大数）时，输出 Z=1。当 X=1 时，按照减 1 规律从 10→01→00→10 循环变化，并每当转换为 00 状态（最小数）时，输出 Z=1。 所以该电路是一个可控的 3 进制计数器，当 X=0 时，作加法计数，Z 是进位信号；当 X=1 时，作减法计数，Z 是借位信号。 三．异步时序电路的分析举例 由于在异步时序逻辑电路中，没有统一的时钟脉冲，因此，分析时必须写出时钟方程。 【例 5-3】试分析图 5-11 所示的时序逻辑电路 图 5-11【例 5-3】逻辑电路图 解：（1）写出各逻辑方程式。 表 5-3 X=1 时的状态表 现 态 次态 输出 n Q1 n Q0 1 1 n+ Q 1 0 n+ Q Z 0 0 1 0 1 1 0 0 1 0 0 1 0 0 0 图 5-8 X=1 时的状态图 00 01 10 0/0 0/0 0/1 1/1 1/0 1/0 图 5-9 完整的状态图

①时钟方程： CP=CP(FF。由CP下降沿触发) CP=CP=Q(FE、FE由O下降沿触发) ②输出方程：Z=Q (5-9) ③各触发器的驱动方程： J0=K=1:J=g3,K,=1:J2=Q,K2=g (5-10) (2)将各驱动方程代入JK触发器的特性方程，得各触发器的次态方程： Q=Jog"+K2"=1Q"+1Q"=0 O"M=Jo+Ko"=0:o+1.0"=0.o" (5-1) OM=J2o+k.o"=0"O"+o"o"=0"o+o"o"=o" (3)作状态转换表、状态图、时序图 表5-4状态转换表 现态 次态 输出 时钟脉冲 Q:of 08 g1g106 2 CP2 CP CPo 000 001 0 00 1 01 0 0 ↓↓ 0 1 0 0 1 1 0 ↑↓ 0 1 1 0 0 ↓ 100 1 0 1 10 1 0 0 0 根据状态转换表可得状态转换图如图5-12所示，时序图如图5-13所示。 200)n @“@①@@@ 11

①时钟方程： CP CP 0 = （ FF0 由 CP 下降沿触发） CP CP Q 1 2 0 = = （ FF1、 FF2 由 Q0 下降沿触发） ②输出方程： 2 n Z Q= （5-9） ③各触发器的驱动方程： 0 0 J K= =1 ； 1 2 1 , 1 n J Q K = = ； 2 1 2 1 , n n J Q K Q = = （5-10） （2）将各驱动方程代入 JK 触发器的特性方程，得各触发器的次态方程： 1 1 1 1 1 1 1 2 1 1 2 1 2 2 1 2 1 2 1 2 1 2 1 1 0 0 0 1 1 1 1 1 2 2 3 1 1 1 n n n n n n n n n n n n n n n n n n n n n n n n n n Q J Q K Q Q Q Q Q J Q K Q Q Q Q Q Q Q J Q K Q Q Q Q Q Q Q Q Q Q + + +  = + =  +  =    = + = +  =   = + = + = + =  （5-11） （3）作状态转换表、状态图、时序图 表 5-4 状态转换表 现态 次态 输出 时钟脉冲 2 n Q n Q1 n Q0 1 2 n Q + 1 1 n+ Q 1 0 n+ Q Z CP2 CP1 CP0 0 0 0 0 0 1 0 ↑ ↑ ↓ 0 0 1 0 1 0 0 ↓ ↓ ↓ 0 1 0 0 1 1 0 ↑ ↑ ↓ 0 1 1 1 0 0 0 ↓ ↓ ↓ 1 0 0 1 0 1 1 ↑ ↑ ↓ 1 0 1 0 0 0 1 ↓ ↓ ↓ 根据状态转换表可得状态转换图如图 5-12 所示，时序图如图 5-13 所示

图5-12【例53】状态图 2 图513【例53】时序图 (5)逻辑功能分析 由状态图可知：该电路一共有6个状态，在时钟脉冲作用下，按照加1规律循环 变化，所以是一个异步六进制加法计数器，Z是进位信号，向高位送出一个负跃变的 进位信号。 5.1.2同步时序电路的设计方法 一，同步时序电路的设计步骤 1.根据设计要求，设定状态，导出对应状态转换图或状态转换表。根据设计的具 体要求，确定时序逻辑电路输入变量、输出变量和状态，确定输入变量、输出变量和 状态的含义，以及在时钟脉冲作用下状态之间的转换关系，并标出其相应的转换条件 和输出，用状态转换图或状态转换表来表示。 2.状态化简。原始状态图（表）通常不是最简的，往往可以消去一些多余状态。 消去多余状态的过程叫做状态化简。输入相同时、输出相同、且转换的状态也相同的 状态叫做等价状态。设Si和Sj是原始状态转换图或状态转换表的两个状态，若Si和 Sj在相同的输入信号作用下具有相同的输出，并且可以转换到相同的状态中去，则称 状态Si和状态Sj等价。显然等价状态是冗余的，可以合并为一个状态 3.选择触发器的类型和个数。电路的状态数确定以后，需要确定电路设计所用触 发器的类型和个数。一般来说，选用触发器的功能越强大，则设计的电路越简单。因 为n个触发器共2”个状态组合，所以触发器的个数根据下式确定：2-≤M≤2” 式中：M为电路的状态数，n为所需要触发器的个数。 4.状态分配（状态编码）。触发器的个数确定以后，状态变量的个数也随之确定 如三个触发器有三个状态变量，共有八种取值：000~111。给电路中的每一个状态选 取不同取值代码的过程称为状态编码，也称为状态分配。状态编码完成后，由逻辑抽

图 5-12 【例 5-3】状态图 图 5-13 【例 5-3】时序图 （5）逻辑功能分析 由状态图可知：该电路一共有 6 个状态，在时钟脉冲作用下，按照加 1 规律循环 变化，所以是一个异步六进制加法计数器，Z 是进位信号，向高位送出一个负跃变的 进位信号。 5.1.2 同步时序电路的设计方法 一．同步时序电路的设计步骤 1.根据设计要求，设定状态，导出对应状态转换图或状态转换表。根据设计的具 体要求，确定时序逻辑电路输入变量、输出变量和状态，确定输入变量、输出变量和 状态的含义，以及在时钟脉冲作用下状态之间的转换关系，并标出其相应的转换条件 和输出，用状态转换图或状态转换表来表示。 2.状态化简。原始状态图（表）通常不是最简的，往往可以消去一些多余状态。 消去多余状态的过程叫做状态化简。输入相同时、输出相同、且转换的状态也相同的 状态叫做等价状态。设 Si 和 Sj 是原始状态转换图或状态转换表的两个状态，若 Si 和 Sj 在相同的输入信号作用下具有相同的输出，并且可以转换到相同的状态中去，则称 状态 Si 和状态 Sj 等价。显然等价状态是冗余的，可以合并为一个状态。 3.选择触发器的类型和个数。电路的状态数确定以后，需要确定电路设计所用触 发器的类型和个数。一般来说，选用触发器的功能越强大，则设计的电路越简单。因 为 n 个触发器共 2 n 个状态组合，所以触发器的个数根据下式确定： 1 2 2 n n M −   式中：M 为电路的状态数，n 为所需要触发器的个数。 4.状态分配（状态编码）。触发器的个数确定以后，状态变量的个数也随之确定。 如三个触发器有三个状态变量，共有八种取值：000～111。给电路中的每一个状态选 取不同取值代码的过程称为状态编码，也称为状态分配。状态编码完成后，由逻辑抽

象得到的状态转换图和转换表就具体化了，反映了逻辑电路在时钟脉冲作用下，触发 器状态的变化关系 为了有利于驱动方程的化简，状态编码的三个实用原则是： (①)次态相同，现态相邻，即在相同输入条件下具有相同次态的现态应分配相邻的编 码： (2②)现态相同，次态相邻，即同一现态在相邻输入条件下的不同次态应分配相邻的编 码： (3)输出相同，现态相邻，即在所有输入条件下具有相同输出的现态应分配相邻的编 码。 5.根据编码状态表以及所采用的触发器的逻辑功能，导出待设计电路的输出方程 和驱动方程。用卡诺图表示每个触发器的次态与现态及输入变量之间的关系，求出电 路的状态方程，结合选用触发器的特性方程，求出其驱动方程。用卡诺图表示输出变 量与触发器现态和输入变量之间的关系，求出电路的输出方程。 6.根据输出方程和驱动方程画出逻辑图。 7.检查电路能否自启动。若电路含有无效状态（指没有用到的多余状态），则必须 检查电路是否具有自启动功能。电路处于无效状态时，能够经过有限个时钟脉冲自动 回到有效状态中去，则称电路具有自启动功能。具有自启动功能的电路在上电时或因 干扰脱离正常状态时，能够自动返回到有效状态。自启动功能是时序逻辑电路设计的 个基本要求。 二.同步时序电路的设计举例 【例5-4】设计一个同步5进制加法计数器 解：设计步骤如下。 (1)根据设计要求，设定状态，画出状态转换图。由于是5 进制计数器，所以应有5个不同的状态，分别用S、S、.、S,表 示。在计数脉冲CP作用下，5个状态循环翻转，在状态为S时， 进位输出Z=1。状态转换图如图5-14所示。 图5-14状态图 (2)状态化简。5进制计数器应有5个状态，不须化简。 (3)状态分配，列状态转换编码表。由式2”≥W>2r可知，应采用3位二进制 代码。该计数器选用三位自然二进制加法计数编码，即S=000、S=001、·、S=100。 由此可列出状态转换表如表5-5所示。 表5-5状态转换表 现态 次态 进位输出 状态转换顺序 Q5 of Q8 gg1Q6* So 0 00 0 01 0

象得到的状态转换图和转换表就具体化了，反映了逻辑电路在时钟脉冲作用下，触发 器状态的变化关系。 为了有利于驱动方程的化简，状态编码的三个实用原则是： (1)次态相同，现态相邻，即在相同输入条件下具有相同次态的现态应分配相邻的编 码； (2)现态相同，次态相邻，即同一现态在相邻输入条件下的不同次态应分配相邻的编 码； (3)输出相同，现态相邻，即在所有输入条件下具有相同输出的现态应分配相邻的编 码。 5.根据编码状态表以及所采用的触发器的逻辑功能，导出待设计电路的输出方程 和驱动方程。用卡诺图表示每个触发器的次态与现态及输入变量之间的关系，求出电 路的状态方程，结合选用触发器的特性方程，求出其驱动方程。用卡诺图表示输出变 量与触发器现态和输入变量之间的关系，求出电路的输出方程。 6.根据输出方程和驱动方程画出逻辑图。 7.检查电路能否自启动。若电路含有无效状态(指没有用到的多余状态)，则必须 检查电路是否具有自启动功能。电路处于无效状态时，能够经过有限个时钟脉冲自动 回到有效状态中去，则称电路具有自启动功能。具有自启动功能的电路在上电时或因 干扰脱离正常状态时，能够自动返回到有效状态。自启动功能是时序逻辑电路设计的 一个基本要求。 二．同步时序电路的设计举例 【例 5-4】设计一个同步 5 进制加法计数器 解：设计步骤如下。 （1）根据设计要求，设定状态，画出状态转换图。由于是 5 进制计数器，所以应有 5 个不同的状态，分别用 S0、S1、.、S4 表 示。在计数脉冲 CP 作用下，5 个状态循环翻转，在状态为 S4 时， 进位输出 Z=1。状态转换图如图 5-14 所示。 （2）状态化简。5 进制计数器应有 5 个状态，不须化简。 （3）状态分配，列状态转换编码表。由式 2 n≥N＞2 n-1 可知，应采用 3 位二进制 代码。该计数器选用三位自然二进制加法计数编码，即 S0=000、S1=001、.、S4=100。 由此可列出状态转换表如表 5-5 所示。 表 5-5 状态转换表 状态转换顺序 现 态 次态 进位输出 n Q2 n Q1 n Q0 1 2 n+ Q 1 1 n+ Q 1 0 n+ Q Z S0 0 0 0 0 0 1 0 S 0 1 S 2 S S 3 4 S 图 5-14 状态图