《数字电子技术》课程教学课件（PPT讲稿）第三章 组合逻辑电路 CH32 加法器和数值比较器

3.2加法器和数值比较器 3.2.1 加法器 一、半加器和全加器 1.半加器（Half Adder) 两个1位二进制数相加不考虑低位进位。 A+B;=S;(和)→C:(进位) A B 函数式 真值表 0 0 0 0 S=AB+AB 0 =A⊕B Ci=AiBi

3.2 加法器和数值比较器 3.2.1 加法器 一、半加器和全加器 1. 半加器（Half Adder） 两个 1 位二进制数相加不考虑低位进位。 Ai Bi Si Ci 0 0 0 1 1 0 1 1 0 0 1 0 1 0 0 1 Si = Ai Bi + Ai Bi Ci = Ai Bi 真 值 表 函数式 = A B Ai+Bi = Si (和) → Ci (进位)

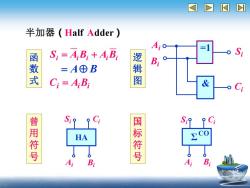
DI 半加器（Half Adder) S:=AB:+AB Bi 数式 =A⊕B Ci=AiBi 逻辑图 C 曾用符号 HA 国标符号 S:9 9Ci A B

逻辑图 曾用符号 国标符号 半加器 （ Half Adder ） Si & A i B i =1 Ci Σ CO SiA i B iCi HA Si A i B iCi S i = A i B i + A i B i Ci = A i B i 函数式 = A  B

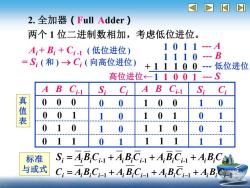
2.全加器(Full Adder) 两个1位二进制数相加，考虑低位进位。 A:+B:+C:.1(低位进位) 1011-A 1110-B =S:(和)→C:(向高位进位) +11100 低位进位 高位进位←-1100 1 -S A B Ci-1 S C A B Ci-1 S C 0 0 0 0 0 1 0 0 0 表 0 01 1 0 10 1 0 0 1 0 1 0 11 0 0 DEBAHBBAESNNNAANANAANNAANAAANNNAA MAAAAAAAAANAAAAAAAMAMAAAAAMA 0 1 1 0 1 111 1 标准 S:=4BC+4BCi+4B.Ci+4B.C 与或式 C=AB:Ci1+A BCi-1+AB:C+ABi

2. 全加器（Full Adder） 两个 1 位二进制数相加，考虑低位进位。 Ai + Bi + Ci -1 ( 低位进位 ) = Si ( 和 ) → Ci ( 向高位进位) 1 0 1 1 - A 1 1 1 0 - B + - 低位进位 0 1 1 0 0 1 1 1 1 真 值 表 Si = Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 Ci = Ai Bi Ci−1 + Ai Bi Ci−1 + Ai Bi Ci−1 + Ai Bi Ci−1 标准 与或式 A B Ci-1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 Si Ci A B Ci-1 Si Ci 0 0 1 0 1 0 0 1 1 0 0 1 0 1 1 1 高位进位← - S 0

全加器（Full Adder) 卡诺图 S BC A 0 011110 ©C00L1"10 0 0 f1 ① 最简与或式 圈 ”1 [S:=4BCi+4BC+4BC+4B;Ci C=AB+AC+BC 圈 0S-4BC+4BC+4BC+4B C=4B+4C-1+BC-

卡诺图 全加器（Full Adder） A BC 0 1 00 01 11 10 1 1 1 1 Si A BC 0 1 00 01 11 10 1 1 1 1 Ci 圈 “ 0 ” Si = Ai Bi Ci−1 + Ai Bi Ci−1 + Ai Bi Ci−1 + Ai Bi Ci−1 Ci = Ai Bi + Ai Ci−1 + Bi Ci−1 Si = Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 + Ai Bi Ci-1 Ci = Ai Bi + Ai Ci−1 + Bi Ci−1 最简与或式 圈 “ 1

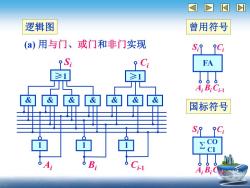
I 逻辑图 曾用符号 (a)用与门、或门和非门实现 C FA A:BiCi- 商离风®卤卤感 国标符号 S99 A:BC

逻辑图 (a) 用与门、或门和非门实现 曾用符号 国标符号 Σ CO CI Si Ai BiCi-1 Ci FA Si Ai BiCi-1 Ci & & & & & & & ≥1 1 1 1 Ai Si Ci Bi Ci-1 ≥1

☒D☒I (b)用与或非门和非门实现 S:=ABCi1+ABCi+AB;Ci+A BCi- C:=ABi+ACi+BCi- ≥1 ≥1 & & B i

(b) 用与或非门和非门实现 Si = Ai Bi Ci−1 + Ai Bi Ci−1 + Ai Bi Ci−1 + Ai Bi Ci−1 Ci = Ai Bi + Ai Ci−1 + Bi Ci−1 & ≥1 & ≥1 1 1 1 Ci Si Ai Bi Ci-1

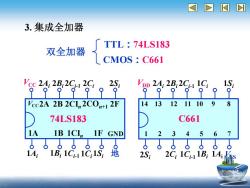
3.集成全加器 TTL 74LS183 双全加器 CMOS:C661 Vcc2A;2B,2C12Ci。 n2A;2B,2C11C;。1S: 9999999 99999 Q Vec2A 2B 2CI 2CO+1 2F 14131211109 8 74LS183 C661 1A 1B 1CI 1F GND 1 2345 6 1B:1Ci 1C:1S 2S: 2C:1C1B:1A:

3. 集成全加器 TTL：74LS183 CMOS：C661 双全加器 74LS183 VCC 2Ai 2Bi 2Ci-1 2Ci 2Si VCC 2A 2B 2CIn 2COn+1 2F 1A 1B 1CIn 1F GND 1Ai 1Bi 1Ci-1 1Ci 1Si 地 1 2 3 4 5 6 7 14 13 12 11 10 9 8 C661 VDD 2Ai 2Bi 2Ci-1 1Ci 1Si 2Si 2Ci 1Ci-1 1Bi 1Ai VSS

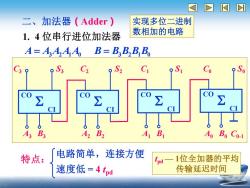
DI 二、加法器 Adder 实现多位二进制 1.4位串行进位加法器 数相加的电路 A=A444 B=B.B,B Bo o S3 0S2 C S1 Co S0 ∑ A3 B3 A,B, A B A0B0C0-1 特点： 电路简单，连接方便 1位全加器的平均 速度低=4tpd 传输延迟时间

二、加法器（Adder） 实现多位二进制 数相加的电路 1. 4 位串行进位加法器 特点： 电路简单，连接方便 速度低 = 4 tpd tpd — 1位全加器的平均 传输延迟时间 A = A3 A2 A1 A0 B = B3 B2 B1 B0 C0 S0 A0 B0 C0-1 CO S CI C1 S1 A1 B1 CO S CI C2 S2 A2 B2 CO S CI C3 S3 A3 B3 CO S CI

2.超前进位加法器 作加法运算时，总进位信号由输入二进制数直接 产生。 Co=AoBo+(o+Bo)Co-1 C=AB+(A+B)Co =4B+(+B)4B+(4+B)Co- C=AB+(A+B)C 特点 应用举例 优点： 速度快 缺点：电路比较复杂 8421BCD码→余3

2. 超前进位加法器 作加法运算时，总进位信号由输入二进制数直接 产生。 0 0 0 0 0 0 1 ( ) C = A B + A + B C − 1 1 1 1 1 0 C = A B + (A + B )C   1 1 1 1 0 0 0 0 0 1 ( ) ( ) = A B + A + B A B + A + B C − 特点 优点：速度快 缺点：电路比较复杂 应用举例 8421 BCD 码→ 余 3 码 1 ( ) Ci = Ai Bi + Ai + Bi Ci−

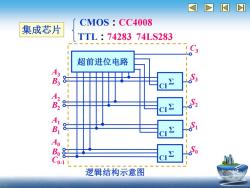
CMOS CC4008 集成芯片 TTL:7428374LS283 超前进位电路 逻辑结构示意图

逻辑结构示意图 集成芯片 CMOS：CC4008 TTL：74283 74LS283 超前进位电路 Σ S3 Σ S2 Σ S1 Σ S0 C3 A3 B3 A2 B2 A1 B1 A0 B0 C0-1 CI CI CI CI