《生物药剂学与药物动力学》课程教学资源（PPT课件）10 重复给药

第十章 重复给药

第十章 重复给药

重复给药·定义：按照一定剂量、一定给药间隔经过多次重复给药，达到并维持有效治疗血药浓度的范围内。·例如：奥司他韦胶囊（达菲，抗病毒药）规格：每粒含主药75mg用量：一次75mg，一日2次2025/8/15heuu-lxn

2025/8/15 heuu-lxn 2 重复给药 • 定义：按照一定剂量、一定给药间隔， 经过多次重复给药，达到并维持有效治 疗血药浓度的范围内。 • 例如： 奥司他韦胶囊（达菲，抗病毒药） 规格：每粒含主药75mg 用量：一次75mg ，一日2次

第一节重复给药血药浓度与时间的关系

第一节 重复给药血药浓度 与时间的关系

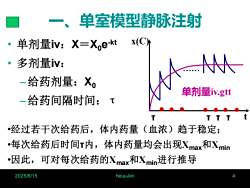
单室模型静脉注射一x(C) 单剂量iv：X=X,e-kt多剂量iv：..一给药剂量：X。单剂量iv.gtt一给药间隔时间：·经过若干次给药后，体内药量（血浓）趋于稳定；·每次给药后时间T内，体内药量均会出现Xmax和Xmin·因此，可对每次给药的Xmax和Xmin进行推导2025/8/15heuu-Ixn

2025/8/15 heuu-lxn 4 一、单室模型静脉注射 • 单剂量iv：X＝X0e -kt • 多剂量iv： –给药剂量：X0 –给药间隔时间：τ t x(C) ● ● ● ● ● ● ● •经过若干次给药后，体内药量（血浓）趋于稳定； •每次给药后时间τ内，体内药量均会出现Xmax和Xmin •因此，可对每次给药的Xmax和Xmin进行推导 ······ 单剂量iv.gtt τ τ τ τ

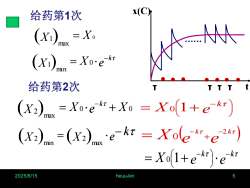
给药第1次= XXi)maxk(x)= Xo'emn给药第2次K=Xo·e-kt+Xo = Xo(1+eX2)Vmaxe-kt = Xole-k2kt(x2)mn = (X2).maxktKT= Xo(1+ee2025/8/15heuu-lxn

2025/8/15 heuu-lxn 5 ( ) 0 1 max X = X 0 0 2 max (X ) X e X k =  + −  X X e −k = 0  1 min ( ) 给药第1次 t x(C) ● ● ● ● ● ● ● ······ 给药第2次 τ τ τ τ e k X X −  ( ) = ( )  2 max 2 min       − = X + e k 0 1 X e e k −k       − = 0 1+  ( ) X e e k 2k 0 − − = +

给药第3次-2kt(x3)= Xo+(X2)min = Xo(1+e-kt-KT+emax-2ktkT-3kt-kt-kt = XolX3)Xe++eleeminmax给药第n次-2kt(n-1)kz= Xo(1+e-k(Xn)max+eLLmax-2kt-3ktnktkt=Xote(Xn)mefee-2025/8/15heuu-Ixn

2025/8/15 heuu-lxn 6 ( ) ( 2) min 3 max X = X 0 + X X X e −k ( ) = ( )  3 max 3 min       − − = X + e + e k 2k 0 1 给药第3次 给药第n次 X X ( e e e ) k k n k n  2  ( 1)  0 max ( ) 1 − − − − = + + ++       − − − = X e + e + e k 2k 3k 0       − − − − X = X e + e + e + + e k k k n k n  2  3    0 min ( ) ······

(n-1)kt-2kt +...+e(Xx)mx = Xo(1+e*kt +e22kt3kt-nkt-KT(X)mn = Xole+eO11-2kt-kt-(n-1)kt令 r=l+ee+e+-2kt-kt-kt-3kt-nkt②er.efe=ete-nkt①一?1-ekt-nkzW-1-er-r:e-kt1-e-nkt-nktCe-kt(Xn) max = Xo(Xn) min = Xoe-kt-kt1-e1-e2025/8/15heuu-Ixn

2025/8/15 heuu -lxn 7 r e e e k 2 k ( n 1 ) k 1 − − − − = + + +  + ee r k nk−− −− = 11 r e e e e e − k − k − k − k −nk  = + + ++ 2 3 令 ①② ① — ② r r e e − k −nk −  = 1 − X X ( e e e ) k k n k n  2  ( 1)  0 max ( ) 1 − − − − = + + +  +   − − − − X = X e + e + e + + e k k k n k n  2  3    0 min ( ) ee X X k n k n  −− −− =  11 ( ) max 0 e ee X X k k n k n   − −− =  −−  11 ( ) min 0

重复给药血药浓度和时间关系-nktekt-ktXn = (Xn)Xomax:ee-ktIe-nktXo1-ee-ktCn =:ektV1-e-nktnkzXoXo1eekt(Cn) maxCnemir-kt-ktVV1-1-ee2025/8/15heuu-Ixn

2025/8/15 heuu-lxn 8 重复给药血药浓度和时间关系 X X e kt n n − = ( ) max e e e X kt k n k − − −  − − =    1 1 0 e e e V X C kt k n k n − − −  − − =    1 0 1 e e V X C k n k n   − − − − =  1 1 ( ) 0 max ( ) e e e V X C k k n k n    − − −  − − =  1 0 1 min

多剂量函数（多剂量因子）给药次数n-nkt1-ek一级消除速率常数V=-kt1-eT给药间隔时间意义：当已知单剂量给药X-t(C-t)时，只需在含的指数项乘以r，即可得到多剂量给药的关系式2025/8/15heuu-lxn

2025/8/15 heuu-lxn 9 多剂量函数（多剂量因子） • 意义：当已知单剂量给药X-t (C-t)时，只需 在含t的指数项乘以r，即可得到多剂量给药 的关系式 e e r k n k   − − − − = 1 1 n 给药次数 k 一级消除速率常数 τ 给药间隔时间

单室iv-nkte-kt= Xo-kXn= Xo·ee-kt1-e-nkt一?e-kt-ktCn= Co·er= Coe-kt1-e102025/8/15heuu-lxn

2025/8/15 heuu-lxn 10 C C e r kt n =   − 0 e e e C kt k n k − − −  − − =    1 1 0 单室 iv X X e r kt n =   − 0 e e e X kt k n k − − −  − − =    1 1 0