《生物药剂学与药物动力学》课程教学资源（PPT课件）08 单室模型

第八章单室模型

第八章 单室模型

单室模型KXoX·药物通过各种途径进入体内，在体内迅速分布到全身的组织器官，达到一种分布上的动态平衡，此时把整个机体视为一个隔室，称之为单室模型2025/8/15heuu-lxn

2025/8/15 heuu-lxn 2 单室模型 • 药物通过各种途径进入体内，在体内 迅速分布到全身的组织器官，达到一 种分布上的动态平衡，此时把整个机 体视为一个隔室，称之为单室模型。 X X0 K

(iv)第一节静脉注射·血管内给药，注射给药后，药物直接入血，不存在吸收，很快随着血液循环分布到全身组织，体内基本只存在消除过程。，药动学研究中最简单的给药途径。研究方法：血药浓度法和尿药法2025/8/15heuu-Ixn

2025/8/15 heuu-lxn 3 • 血管内给药，注射给药后，药物直接 入血，不存在吸收，很快随着血液循 环分布到全身组织，体内基本只存在 消除过程。 • 药动学研究中最简单的给药途径。 ➢ 研究方法：血药浓度法和尿药法 第一节 静脉注射（iv）

解微分方程C-t关系建模型列速度式模型参数2025/8/15heuu-lxn

2025/8/15 heuu-lxn 4 建模型 列速度式 模型 参数 解微分方程 C-t关系

血药浓度法一、1、建模型列速度式dXXo=-kXkXdtdX：体内药物的X。：给药剂量X：在时间t时的体内药量，dt消除速率k：一级消除速率常数2025/8/15heuu-Ixn

2025/8/15 heuu-lxn 5 一、血药浓度法 X X0 k 1、建模型 X0 ：给药剂量 X：在时间t时的体内药量， k：一级消除速率常数 列速度式 kX dt dX = − dt dX ： 体内药物的 消除速率

2、血药浓度与时间关系求解解微分方程拉普拉斯变换dX=-kXL[X]= Xdt拉变：sX - X(0) = -kxiv，当t= 0时,X(O)= XAe-atX。查拉氏变换表X-A-Xo， a=ks+k2025/8/15heuu-lxn

2025/8/15 heuu-lxn 6 2、血药浓度与时间关系 kX dt dX = − 拉普拉斯变换 求解 拉变： s k X X + = 0 iv，当 t = 0时， 查拉氏变换表 sX − X(0) = −kX 0 X(0) = X L[X ] = X Ae-at A=X0，a=k 解微分方程

拉普拉斯变换The Laplace Transform微分方程>拉氏变换法求解。中·拉氏变换过程：微分方程象函数的代数方程逆变换原微分方程的解象函数F（s）2025/8/15heuu-lxn

2025/8/15 heuu-lxn 7 拉普拉斯变换 The Laplace Transform • 微分方程→拉氏变换法求解。 • 拉氏变换过程： 微分方程 象函数的代数方程 象函数F(s) 原微分方程的解 逆变换

定义：函数f(t)的拉变式f(t)e-stdtF(s) = L[f(t) | =0拉普拉斯变换符号LI: 象函数，原函数f(t)的拉氏变换F(s):拉氏运算子S:2025/8/15heuu-Ixn

2025/8/15 heuu-lxn 8   − 0 f (t)e dt st F(s) = L[ f(t) ] = L[ ]：拉普拉斯变换符号 F(s)：象函数，原函数f(t)的拉氏变换 s：拉氏运算子 定义：函数f(t)的拉变式

拉式变换性质常数：L[A]=A/s，常数与原函数积：L[A,f(t)] =A L[f(t))函数和 : L[fi(t) +f2(t)] = Lfi[(t)] + Lf2[(t)] 原函数导数 :L[f'(t)] =s L[f(t)] -f(O) 指数函数：L[e -atl= 1/(s+a)2025/8/15heuu-Ixn

2025/8/15 heuu-lxn 9 拉式变换性质 • 常数：L[A] = A/s • 常数与原函数积：L[A f(t)] = A L[f(t)] • 函数和：L[f1 (t) + f2 (t)] = Lf1 [(t)] + Lf2 [(t)] • 原函数导数：L[f ’(t)] = s L[f(t)] – f(0) • 指数函数：L[e –at ] = 1 / (s+a)

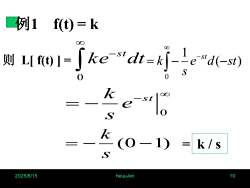
例1f(t) = k88ke-st dt=ke-st d(-st)则 L[f(t)] =Ses00k8ste10Sk(0-1)k/sS102025/8/15heuu-Ixn

2025/8/15 heuu-lxn 10 例1 f(t) = k 则 L[ f(t) ] =   − 0 k e dt st  − = − 0 s t e s k = k / s   − = − − 0 ( ) 1 e d st s k st = − (0 −1) s k