《生物药剂学与药物动力学》课程教学资源(PPT课件)09 多室模型

第九章多室模型
第九章 多室模型

脑双室模型药物一血,向体内各部位分布速度不同脂溶性药物>分布快,时间可忽略不计,这些组织器官和体液构成一个隔室,称“中央室血浆等);(心、肝、脾、肺、肾、』>药物分布到另一部分组织、器官和体水溶性药物分布较慢,称“周边室”或“外室”(肌肉、骨骼、皮下脂肪)。2025/8/15heuu-lxn
2025/8/15 heuu-lxn 2 双室模型 药物→血,向体内各部位分布速度不同 ➢分布快,时间可忽略不计,这些组织、 器官和体液构成一个隔室,称“中央室” (心、肝、脾、肺、肾、血浆等); ➢药物分布到另一部分组织、器官和体液, 分布较慢,称“周边室”或“外室” (肌肉、骨骼、皮下脂肪)。 脑 脂 溶 性 药 物 水 溶 性 药 物

第一节二室模型血管内给药静脉注射血药浓度法2025/8/15heuu-Ixn
2025/8/15 heuu-lxn 3 第一节 二室模型血管内给药 一、静脉注射 • 血药浓度法
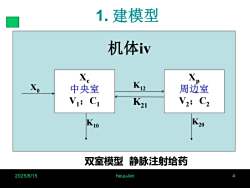
1.建模型机体ivX.X.K12Xo周边室中央室Vr; CiK21V2; C2K-20K10双室模型静脉注射给药2025/8/15heuu-Ixn
2025/8/15 heuu-lxn 4 Xc 中央室 V1;C1 Xp 周边室 V2;C2 K12 K21 K10 X0 机体iv 双室模型 静脉注射给药 1. 建模型 K20

2.列速度式·药物在中央室的变化速度dX= k21: X, - k12· X- k1o · X ①dt,药物在周边室的变化速度dX,= k12: X。- k21· X,. @dt2025/8/15heuu-Ixn
2025/8/15 heuu-lxn 5 2. 列速度式 • 药物在中央室的变化速度 • 药物在周边室的变化速度 p c c c k X k X k X dt d X = 2 1 − 1 2 − 1 0 c p p p k X k X k X dt dX = 1 2 − 2 1 − 2 0 ① ②

:t=0时,iv的药物迅速完全进入中央室:.X.=Xo , X,=0dXc①拉变 k21.Xp- ki2. Xc- kio· XcdtsL[xe ]- Xe(O)= k2iL[xp]- k12L[xe] -k10L[xe](s + k12 + k10)L[xc]- k2iL[Xp]= Xc(O)(s + k12 + k10)Lxc k2iLXp= X0 (32025/8/15heuu-lxn
2025/8/15 heuu-lxn 6 p c c c k X k X k X dt dX ①拉变 = 2 1 − 1 2 − 1 0 sLxc− xc(0)= k21Lxp−k12Lxc−k10Lxc (s + k12+ k10)Lxc−k21Lxp= xc(0) (s + k12+ k10)Lxc−k21Lxp= x0 ③ ∵t=0时,iv的药物迅速完全进入中央室 ∴Xc=X0,Xp=0

dXp②拉变= k12 : X- k21 X,dtsL[xp]- Xp(O)= k12L[xe]-k2iL[xp](s + k21]L[xp]-k12L[xe] = 0L[x ] = ki2L[x0]④s + k212025/8/15heuu-Ixn
2025/8/15 heuu-lxn 7 c p p k X k X dt dX = 1 2 − 2 1 ②拉变 sLxp− xp(0) = k12Lxc−k21Lxp (s +k21)Lxp−k12Lxc= 0 2 1 1 2 c p k k L x L x + = s ④

k12L/Xc将④代入③:(s + k12 + k1o)L[xc|- k21Xos +k21S+k21Lel hhhh: X0?设αβ=k10·k21α+β= k12 +k21+k10s+k21L[x0]= (s+a)(6+p) x0查表?(Xo.α -X。. k2i)e-" +(Xo. k21- Xo.β)e-Xc :α-β2025/8/15heuu-xn
2025/8/15 heuu-lxn 8 将④代入③: ( ) 0 2 1 1 2 c 1 2 1 0 c 2 1 x L x s k k L x k = + + + − s k k = k10 k 21 ( ) 0 1 2 2 1 1 0 1 0 2 1 2 2 1 L xc x + + + + + = k k k s k k s k s + = k1 2 + k 2 1+ k1 0 ( )( ) 0 2 1 L xc x + + + = s s s k ⑤ 设 查表 ( ) ( ) − − + − = − − e e t t X X k X k X Xc 0 0 2 1 0 2 1 0

Xo(α - k2iXo(k21- β)中央室药量-βtXc =与时间关系Xee(Xct)α-βα-βXo(k21-β)Xo(α - k21)-βtαC:eeV(α-β)V(α-β)Xo(k21 - β)Xo(α - k21)设A :B =V(α-β)V(α-β)+Be-βt-xtC=Ae中央室药物浓度与时间关系(C一t)双指数方程2025/8/15heuu-Ixn
2025/8/15 heuu-lxn 9 ( ) ( ) ( ) ( ) e e t t V X k V X k C − − − − + − − = 0 2 1 0 2 1 中央室药物浓度与时间关系(C—t) 双指数方程 设 ( ) ( ) − − = V X k A 0 21 ( ) ( ) − − = V X k B 0 21 e e t t C A B − − = + ( ) ( ) e e X k t X k t Xc − − − − + − − = 0 2 1 0 2 1 中央室药量 与时间关系 (XC—t)
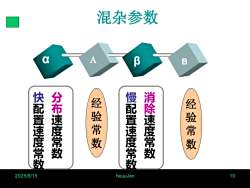
混杂参数aβA消除速度常数慢配置速度常数快配置速度常数分布速度常数经验常数经验常数2025/8/1510heuu-lxn
2025/8/15 heuu -lxn 10 α A B 分布速度常数 快配置速度常数 β 消除速度常数 慢配置速度常数 混杂参数 经验常数 经验常数
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《生物药剂学与药物动力学》课程教学资源(专家讲座)PEG化生物技术药物的研究与开发(PPT).ppt
- 《生物药剂学与药物动力学》课程教学资源(专家讲座)创新药物及其代谢物浓度测定方法的建立及应注意的问题(PPT,中国科学院上海药物研究所:钟大放).ppt
- 《生物药剂学与药物动力学》课程教学资源(专家讲座)新药药代动力学的若干问题(PPT,皖南医学院:孙瑞元).ppt
- 《生物药剂学与药物动力学》课程教学资源(专家讲座)药物基因组学的研究及应用进展(PPT).ppt
- 《生物药剂学与药物动力学》课程教学资源(专家讲座)General Clinical Pharmacokinetics Review 2(PPT).ppt
- 《生物药剂学与药物动力学》课程教学资源(专家讲座)The Laplace Transform(PPT,沈阳药科大学).ppt
- 《生物药剂学与药物动力学》课程教学资源(专家讲座)How to Expand Routine Bioequivalence Studies to Generate New Knowledge(PPT).ppt
- 《生物药剂学与药物动力学》课程教学资源(专家讲座)浅谈中药药代动力学(PPT).ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT讲稿)药代动力学与生物利用度(华中科技大学:严常开).ppt
- 《生物药剂学与药物动力学》课程教学资源(参考书籍)中国药典《中华人民共和国药典》书籍PDF电子版(2010年版,第一部药材).pdf
- 《生物药剂学与药物动力学》课程教学资源(PPT讲稿)药物代谢与细胞色素P450.ppt
- 《生物药剂学与药物动力学》课程教学资源(文献资料)微透析技术及其在药动学中应用.doc
- 《生物药剂学与药物动力学》课程教学资源(文献资料)代谢组学_一个迅速发展的新兴学科_英文_唐惠儒.pdf
- 《生物药剂学与药物动力学》课程教学资源(文献资料)非线性药物动力学参数的计算方法研究进展_蔡晔.pdf
- 《生物药剂学与药物动力学》课程教学资源(文献资料)_指纹药动学_的构思与研究_易延逵.pdf
- 《生物药剂学与药物动力学》课程教学资源(文献资料)HPLC法测定人血浆中奥沙普秦含量及其药物动力学_谢伟.pdf
- 《生物药剂学与药物动力学》课程教学资源(文献资料)血管外给药的非线性房室模型解的逼近_胡晓虎.pdf
- 《生物药剂学与药物动力学》课程教学资源(文献资料)万古霉素群体药物动力学模型的研究进展_何笑荣.pdf
- 《生物药剂学与药物动力学》课程教学资源(文献资料)代谢组学在中医药研究中的应用进展_高鹏飞.pdf
- 《生物药剂学与药物动力学》课程教学资源(文献资料)谈微分方程在药物动力学方面的应用_蒋长安.pdf
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)08 单室模型.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)07 药物动力学概述.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)06 药物排泄.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)05 药物代谢.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)04 药物的分布.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)01 绪论 Biopharmaceutics and Pharmacokinetics(华北理工大学:李小娜).ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)03 非口服给药的吸收.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)02 口服 第一节 药物的膜转运与胃肠道吸收.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)02 口服 第二节 影响药物吸收的因素 第三节 口服药物吸收与制剂设计 第四节 口服药物吸收的.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)12 统计矩原理在药物动力学研究中的应用.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)11 非线性药物动力学.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)14 新药的药物动力学研究.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)13 药物动力学在临床药学中的应用.ppt
- 《生物药剂学与药物动力学》课程教学资源(PPT课件)10 重复给药.ppt
- 《药物分析》课程教学大纲 pharmaceutical analysis.doc
- 《药物分析》课程授课教案(讲稿)第十八章 药物制剂的分析、第十九章 中药及其制剂分析概论.doc
- 《药物分析》课程授课教案(讲稿)第十四章 维生素类药物的分析.doc
- 《药物分析》课程授课教案(讲稿)第十五章 甾体激素类药物的分析、第十六章 抗生素类药物的分析.doc
- 《药物分析》课程授课教案(讲稿)第十二章 喹啉类与青蒿素类抗疟药物的分析、第十三章 莨菪烷类抗胆碱药物的分析.doc
- 《药物分析》课程授课教案(讲稿)第十一章 吩噻嗪类抗精神病药物的分析.doc
