《流体力学》课程授课教案（讲义）第三章 流体动力学基础

第三章流体动力学基础 本章研究流体运动的基本规律及其在工程中的应用基础，介绍流体动力学的基本知识、 基木原理和基本方程。 第一节描述流体运动的两种方法 表征运动流体的物理量称为流体的流动参数。描沭流体运动就是要表法流体质点的流动 参数在不同空间位置上随时间连续变化的规律。在流体力学中，描述流体运动的方法有拉格 朗日(Lagrange)法和欧拉(Euler)法。 一、拉格朗日法 充满流体质点运动的空间称为流场。拉格朗日法从分析流体质点的运动着手，分析流动 参数随时间的变化规律，然后综合所有被研究流体质点的运动情况来获得整个流体运动的规 律。这种方法与理论力学中描述质点或质点系的方法一样。显然，这个方法可以了解每个流 体质点的运动规律 由于拉格朗日方法着眼于每个流体质点，需要找到一种方法用以区分不同的流体质点。 通常采用的方法是以初始时刻1。时，各质点的空间坐标(a,b,c)作为不同质点的区别 标志。在流体运动过程中，每一个质点的运动坐标不是独立变量，而是起始坐标(a,b,c) 和时间变量t的函数。人们把a,b,c,1叫做拉格朗日变数 流体质点的空间位置(x,y,:),可以表示为 x=x(a,b.c,t) y=ya,b,c,1) (3-1) =(a,b,c,t） 运动坐标对时间求导，则可得流体质点的速度 1,-dreexfa.b.c!) d at (a,b,c,1) (3-2 dt Gt ot =正_z(a,b,c,i) d 变数，把1看成常数，将得到1时刻流体质点的速度分布。 流体质点的加速度为 1

1 第三章 流体动力学基础 本章研究流体运动的基本规律及其在工程中的应用基础，介绍流体动力学的基本知识、 基本原理和基本方程。 第一节 描述流体运动的两种方法 表征运动流体的物理量称为流体的流动参数。描述流体运动就是要表达流体质点的流动 参数在不同空间位置上随时间连续变化的规律。在流体力学中，描述流体运动的方法有拉格 朗日(Lagrange)法和欧拉(Euler)法。 一、拉格朗日法 充满流体质点运动的空间称为流场。拉格朗日法从分析流体质点的运动着手，分析流动 参数随时间的变化规律，然后综合所有被研究流体质点的运动情况来获得整个流体运动的规 律。这种方法与理论力学中描述质点或质点系的方法一样。显然，这个方法可以了解每个流 体质点的运动规律。 由于拉格朗日方法着眼于每个流体质点，需要找到一种方法用以区分不同的流体质点。 通常采用的方法是以初始时刻 0 t 时，各质点的空间坐标（ a ， b ， c ）作为不同质点的区别 标志。在流体运动过程中，每一个质点的运动坐标不是独立变量，而是起始坐标（ a ，b ，c ） 和时间变量 t 的函数。人们把 a， b ， c ， t 叫做拉格朗日变数。 流体质点的空间位置（ x, y,z ），可以表示为      = = = ( , , , ) ( , , , ) ( , , , ) z z a b c t y y a b c t x x a b c t （3-1） 运动坐标对时间求导，则可得流体质点的速度 d d d d d d ( , , , ) ( , , , ) ( , , , ) x y z x x x a b c t v t t t y y y a b c t v t t t z z z a b c t v t t t    = = =        = = =        = = =     （3-2） 因为 a,b, c 不随时间变化，所以 t z t z t y t y t x t x   =   =   = d d , d d , d d 。而在微分之后将 a,b, c 看成 变数，把 t 看成常数，将得到 t 时刻流体质点的速度分布。 流体质点的加速度为

a,-产-0a,6c0 01 (3-3) a-.ac 同样流体质点密度p、压力p和温度T等流动参数也可以表示为a,b,c和t的函数 p=p(a.b,c,1) p=p(a.b.c.t) (3-4) T=T(a,b,c,1)) 拉格朗日法可以描述任一流体质点的运动。但是，由于流体质点的运动轨迹非常复杂， 用拉格朗日法去分析流体运动时，方程的建立和数学处理将遇到很多困难。同时，工程上 般也不需要知道给定流体质点的运动规律。因此，除研究台风运动和波浪运动等特殊问题外 流体力学中通常不采用这种方法。 二、欧拉法 欧拉法不同于拉格朗日法。欧拉法的着眼点是空间点，即着眼于流体经过流场中各空间 点时的运动情况，而不关心这些运动特性是由哪些流体质点表现出来的，也不考虑流体质点 的来龙去脉，然后综合空间点上各质点的流动参数及其变化规律，用以描述整个流体的运动。 欧拉法用质点的空间坐标(x,y,:)与时间变量1来表达流场中的流体运动规律， (x,:,)称为欧拉变数。欧拉变数不是各自独立的，因为流体质点的空间位置x,y,:与运 动过程中的时间变量有关。不同的时间，各个流体质点对应不同的空间坐标，因而对任一流 体质点来说，其位置变量x,，：是时间1的函数。因此，流场中各空间点的流速所组成的速度 场可以表示为 v.=v.(x.y.=.0)=v.[().y().:()i] y,=v,(x,y,z,)=v[xy=) (3-5) y:=y(x3,)=v:x00= 由上式可以得到任一时刻（即【一定）流体质点速度在空间中的分布规律，也可以得到 任一空间点（即x,y,:一定）的流体质点速度随时间的变化规律。 同样，各空间点的其它流动参数组成的压强场、密度场、温度场等可以表示为 p=p(x.y.,1) o=D(x.V.3.t) (3-6) T=T(x.y.=.t)] 式(35)和(36)是空间的坐标(x,y,:)的函数，研究的是场，如速度场、压强 场、密度场、温度场等。因此说，采用欧拉法就可以利用场论的知识。 2

2            =   =   =   =   =   = 2 2 2 2 2 2 ( , , , ) ( , , , ) ( , , , ) t z a b c t t v a t y a b c t t v a t x a b c t t v a z z y y x x （3-3） 同样流体质点密度  、压力 p 和温度 T 等流动参数也可以表示为 a ， b ， c 和 t 的函数      = =  =  ( , , , ) ( , , , ) ( , , , ) T T a b c t p p a b c t a b c t （3-4） 拉格朗日法可以描述任一流体质点的运动。但是，由于流体质点的运动轨迹非常复杂， 用拉格朗日法去分析流体运动时，方程的建立和数学处理将遇到很多困难。同时，工程上一 般也不需要知道给定流体质点的运动规律。因此，除研究台风运动和波浪运动等特殊问题外， 流体力学中通常不采用这种方法。 二、欧拉法 欧拉法不同于拉格朗日法。欧拉法的着眼点是空间点，即着眼于流体经过流场中各空间 点时的运动情况，而不关心这些运动特性是由哪些流体质点表现出来的，也不考虑流体质点 的来龙去脉，然后综合空间点上各质点的流动参数及其变化规律，用以描述整个流体的运动。 欧拉法用 质点的 空间坐 标（ x, y,z ）与时 间变量 t 来表达 流场中 的流体 运动规 律， （ x, y,z,t ）称为欧拉变数。欧拉变数不是各自独立的，因为流体质点的空间位置 x, y,z 与运 动过程中的时间变量有关。不同的时间，各个流体质点对应不同的空间坐标，因而对任一流 体质点来说，其位置变量 x, y,z 是时间 t 的函数。因此，流场中各空间点的流速所组成的速度 场可以表示为  ( ) ( ) ( )   ( ) ( ) ( )   ( ) ( ) ( )       = = = = = = v v x y z t v x t y t z t t v v x y z t v x t y t z t t v v x y z t v x t y t z t t z z z y y y x x x ( , , , ) , , , ( , , , ) , , , ( , , , ) , , , （3-5） 由上式可以得到任一时刻（即 t 一定）流体质点速度在空间中的分布规律，也可以得到 任一空间点（即 x, y,z 一定）的流体质点速度随时间的变化规律。 同样，各空间点的其它流动参数组成的压强场、密度场、温度场等可以表示为      =  =  = ( , , , ) ( , , , ) ( , , , ) T T x y z t x y z t p p x y z t （3-6） 式（3-5）和（3-6）是空间的坐标（ x ， y ， z ）的函数，研究的是场，如速度场、压强 场、密度场、温度场等。因此说，采用欧拉法就可以利用场论的知识

下面过论流体质点加速度的表示方法】 欧拉法中空间点的加速度是指某一时刻该空间点的流体质点的加速度，是空间点x,二， 的函数。由于质点本身的位置坐标(x,y,:)也是时间1的函数，因而自变量只有1。所 以说，质点的加速度不是1的简单一元函数，而是1的复合函数，其中间变量就是x=x) y=),z=。按照复合函数求导的法则可求得质点的加速度。 加速度在x方向的分量为 0变+出+等出产出 (3-7)】 dt 质点位置坐标(x,:)对时间的导数就是该质点的速度分量，即 dx 所以，可得加速度在空间坐标x,y:方向的分量 dv (3-8 若用v表示速度矢量、a表示加速度矢量，则上式可表示为 (3-9) 式中，P=i会+导+水是，称为哈密顿第子(opra》,它强然具有矢 量形式，但并非矢量：它只是对其后面所列的函数进行微分运算的一种符号。 由此可见，流体质点的加速度由两部分组成：第一部分”称为当地加速度或时变加速 度，它表示位于所观察点上的流体质点的速度随时间的变化率：第二部分（可加称为迁移加 速度或位变加速度，表示流体质点所在空间位置的变化所引起的速度变化率。两部分之和就 是流体质点的全加速度，又称为随体导数或质点导数，即流体质点速度随时间的变化率。它 们的物理概念可用图31所示的装置加以说明。水流经变径管流出，由于水箱中的水位逐渐 降低，变径管内同一点的流速随时间不断减小：同时，随着管径变小，同一时刻变径管内各 点的流速又沿程增加。前者引起的加速度就是当地加速度，后者引起的加速度就是迁移加速 图3-1 应用欧拉法研究流体运动时，常在流场中选取一个固定的空间区域来观察流体的运动， 这个固定的空间区域称为控制体，它的边界面称为控制面。控制体的形状、体积和位置根据

3 下面讨论流体质点加速度的表示方法。 欧拉法中空间点的加速度是指某一时刻该空间点的流体质点的加速度，是空间点 x, y,z,t 的函数。由于质点本身的位置坐标（ x ， y ， z ）也是时间 t 的函数，因而自变量只有 t 。所 以说，质点的加速度不是 t 的简单一元函数，而是 t 的复合函数，其中间变量就是 x = x(t)， y = y(t)， z = z(t) 。按照复合函数求导的法则可求得质点的加速度。 加速度在 x 方向的分量为 ( ) t z z v t y y v t x x v t v t v x y z t a x x x x x d d d d d d d d , , , x   +   +   +   = = （3-7） 质点位置坐标( x, y,z )对时间的导数就是该质点的速度分量，即 x v t x = d d ， y v t y = d d ， z v t z = d d 所以，可得加速度在空间坐标 x, y,z 方向的分量            +   +   +   = =   +   +   +   = =   +   +   +   = = z v v y v v x v v t v t v a z v v y v v x v v t v t v a z v v y v v x v v t v t v a z x y z y z y y y x y y x z x y x x x x z z z z z y x d d d d d d （3-8） 若用 v 表示速度矢量、 a 表示加速度矢量，则上式可表示为 (v )v v v a +    = = dt t d （3-9） 式中， x y z  +   +    = i j k ，称为哈密顿算子（Hamiltonian operator），它虽然具有矢 量形式，但并非矢量；它只是对其后面所列的函数进行微分运算的一种符号。 由此可见，流体质点的加速度由两部分组成：第一部分 t v 称为当地加速度或时变加速 度，它表示位于所观察点上的流体质点的速度随时间的变化率；第二部分 (v )v 称为迁移加 速度或位变加速度，表示流体质点所在空间位置的变化所引起的速度变化率。两部分之和就 是流体质点的全加速度，又称为随体导数或质点导数，即流体质点速度随时间的变化率。它 们的物理概念可用图 3-1 所示的装置加以说明。水流经变径管流出，由于水箱中的水位逐渐 降低，变径管内同一点的流速随时间不断减小；同时，随着管径变小，同一时刻变径管内各 点的流速又沿程增加。前者引起的加速度就是当地加速度，后者引起的加速度就是迁移加速 度。 图 3-1 应用欧拉法研究流体运动时，常在流场中选取一个固定的空间区域来观察流体的运动， 这个固定的空间区域称为控制体，它的边界面称为控制面。控制体的形状、体积和位置根据

所研究的问题可以任意选取。 在流体力学中常用欧拉法。由前述讨论可知，欧拉法研究的是流场中每个固定空间点上 的流动参数的分布及随时间的变化规律，给出了某瞬时整个流场的流动参数分布，因而可以 用连续函数理论对流场进行有效的理论分析和计算。因为在大多数的工程实际问题中，不需 要知道每个流体质点自始至终的运动过程，只需要知道流体质点在通过空间任意固定点时流 动参数随时间的变化，以及某一时刻流场中各空间固定点上流体质点的流动参数，然后就可 以用数学方法对整个流场进行求解计算。其次，在欧拉法中，数学方程的求解较拉格朗日法 容易。再次，测量流体参数时，用欧拉法可将测试仪表周定在指定的空间点上，这种测量是 容易做到的。 第二节流体运动的基本概念 为了用欧拉法研究流体运动及建立流体动力学基本方程，首先必须了解一些流体运动中 的基本概念。 一、恒定流动与非恒定流动 如果流场中每一空间点上的流动参数都不随时间变化，这种流动就称为恒定流动，又称 为定常流动，否则称为非恒定流动或非定常流动。恒定流动中，流场内的速度、压力、密度 等所有的物理量只是空间坐标x,y,:的函数，与时间变量1无关， 即各流动参数的当地导数为零。 在恒定流动中，因为不包括时间变量1，因而流动的分析较非恒定流动要简单得多。在 实际工程问题中，如果流动参数随时间变化比较缓慢，在满足一定要求的前提下，可以将非 恒定流动作为恒定流动来处理。另外，确定流体运动是恒定流动或非恒定流动，与选取的坐 标系有关。例如，船在静止的水中等速直线行驶，船两侧的水流流动对于站在岸上的人看米 (即对于取固定在岸上的坐标系来讲)是非恒定流，而对于站在船上的人看来（即对于取固 定在船上的坐标系来讲)则是恒定流动。 二、流线与迹线 流体质点运动的轨迹称为迹线，它给出同一质点在不同时刻的速度方向。由迹线的形状 可以清楚地看出质点的流动情况，从而得出流场的参数分布和变化情况，迹线是拉格朗日法 分析流体运动的概念。 在液流中加入颜色不同且不易扩散的液滴，就可以观察到染了色的流体质点的迹线形状。 流线是指某一瞬时在流场中所作的一条假想的空间曲线，在该时刻，位于曲线上各点的 流体质点的速度在各点与流线相切（如图32）

4 所研究的问题可以任意选取。 在流体力学中常用欧拉法。由前述讨论可知，欧拉法研究的是流场中每个固定空间点上 的流动参数的分布及随时间的变化规律，给出了某瞬时整个流场的流动参数分布，因而可以 用连续函数理论对流场进行有效的理论分析和计算。因为在大多数的工程实际问题中，不需 要知道每个流体质点自始至终的运动过程，只需要知道流体质点在通过空间任意固定点时流 动参数随时间的变化，以及某一时刻流场中各空间固定点上流体质点的流动参数，然后就可 以用数学方法对整个流场进行求解计算。其次，在欧拉法中，数学方程的求解较拉格朗日法 容易。再次，测量流体参数时，用欧拉法可将测试仪表固定在指定的空间点上，这种测量是 容易做到的。 第二节 流体运动的基本概念 为了用欧拉法研究流体运动及建立流体动力学基本方程，首先必须了解一些流体运动中 的基本概念。 一、恒定流动与非恒定流动 如果流场中每一空间点上的流动参数都不随时间变化，这种流动就称为恒定流动，又称 为定常流动，否则称为非恒定流动或非定常流动。恒定流动中，流场内的速度、压力、密度 等所有的物理量只是空间坐标 x, y,z 的函数，与时间变量 t 无关， = 0   =   =   =   t T t t p t v  ， 即各流动参数的当地导数为零。 在恒定流动中，因为不包括时间变量 t ，因而流动的分析较非恒定流动要简单得多。在 实际工程问题中，如果流动参数随时间变化比较缓慢，在满足一定要求的前提下，可以将非 恒定流动作为恒定流动来处理。另外，确定流体运动是恒定流动或非恒定流动，与选取的坐 标系有关。例如，船在静止的水中等速直线行驶，船两侧的水流流动对于站在岸上的人看来 （即对于取固定在岸上的坐标系来讲）是非恒定流，而对于站在船上的人看来（即对于取固 定在船上的坐标系来讲）则是恒定流动。 二、流线与迹线 流体质点运动的轨迹称为迹线，它给出同一质点在不同时刻的速度方向。由迹线的形状 可以清楚地看出质点的流动情况，从而得出流场的参数分布和变化情况，迹线是拉格朗日法 分析流体运动的概念。 在液流中加入颜色不同且不易扩散的液滴，就可以观察到染了色的流体质点的迹线形状。 流线是指某一瞬时在流场中所作的一条假想的空间曲线，在该时刻，位于曲线上各点的 流体质点的速度在各点与流线相切（如图 3-2）

图3-2 流线形象地给出了流场中的流动状态，通过流线可以清楚地看出某时刻流场中各点的速 度方向。显然，流线是欧拉法分析流体运动的概念。在流场内可以绘出一簇流线，所构成的 流线图称为流谱。 般情况下（除驻点或奇点），流线具有如下性质 (1)恒定流动中，流线形状不随时间变化，且流体质点的流线与迹线重合： (2)流线不能相交，不能突然转折，只能是一条光滑曲线。否则，在交点或转折点处将 有两个速度矢量，这意味者在同一时刻，同一流体质点具有两个运动方向，这是不可能的。 利用流线不能突然转折的性质，人们经常采用“流线型”来改善运动物体的动力性能」 如图3-3的尾部，由于流线不能突然转折，必然有一部分流体不能随主流一起运动，而被主 流带动产生了旋涡，消耗了能量，增大了运动物体的阻力。如果将物体的尾部改成“流线型”， 则可以减小尾部的旋涡，从而减小运动阻力，改善运动物体的动力性能。 图3.3 由流线的定义，可以建立流线的微分方程。 设流线上某一点的瞬时速度为 v=vi+vrj+vk (3.10) 流线上微元线段矢量为 ds=dxi+dyj+dk (3-11) 根据流线的定义，这两个矢量的方向一致，矢量积为零 vxds=0 (3.12) 写成投影形式，就是流线的微分方程 dr_dy_d正 (3-12) V,Vy V. 因为流线是某一时刻的曲线，所以时间变量1不是自变量，只能作为一个参变量。求某 指定时刻的流线时，需要把1当作常数带入上式，然后进行积分即可求得。 例3-1己知流速场为,=x+1,y,=-y+1,y=0。试求1=0时刻，通过点A(1,-1) 的流线。 解：由式(3-12)，流线的微分方程是 dy 式中，1是参变量，当作常数，对上式积分，得 hc+)=-h(-y+)+hC 得流线方程为 (x+t0-y+)=C 由上式可知，任一瞬时的流线是一双曲线

5 图 3-2 流线形象地给出了流场中的流动状态，通过流线可以清楚地看出某时刻流场中各点的速 度方向。显然，流线是欧拉法分析流体运动的概念。在流场内可以绘出一簇流线，所构成的 流线图称为流谱。 一般情况下（除驻点或奇点），流线具有如下性质： （1）恒定流动中，流线形状不随时间变化，且流体质点的流线与迹线重合； （2）流线不能相交，不能突然转折，只能是一条光滑曲线。否则，在交点或转折点处将 有两个速度矢量，这意味着在同一时刻，同一流体质点具有两个运动方向，这是不可能的。 利用流线不能突然转折的性质，人们经常采用“流线型”来改善运动物体的动力性能。 如图 3-3 的尾部，由于流线不能突然转折，必然有一部分流体不能随主流一起运动，而被主 流带动产生了旋涡，消耗了能量，增大了运动物体的阻力。如果将物体的尾部改成“流线型”， 则可以减小尾部的旋涡，从而减小运动阻力，改善运动物体的动力性能。 图 3-3 由流线的定义，可以建立流线的微分方程。 设流线上某一点的瞬时速度为 v = v x i + vy j + vzk （3-10） 流线上微元线段矢量为 ds = dxi + dyj + dzk （3-11） 根据流线的定义，这两个矢量的方向一致，矢量积为零 vds = 0 （3-12） 写成投影形式，就是流线的微分方程 x y z v z v y v dx d d = = （3-12） 因为流线是某一时刻的曲线，所以时间变量 t 不是自变量，只能作为一个参变量。求某 一指定时刻的流线时，需要把 t 当作常数带入上式，然后进行积分即可求得。 例 3-1 已知流速场为 v x t x = + ，v y t y = − + ，vz = 0 。试求 t = 0 时刻，通过点 A(-1,-1) 的流线。 解：由式（3-12），流线的微分方程是 y t y x t x − + = + d d 式中， t 是参变量，当作常数，对上式积分，得 ln(x +t) = −ln(− y +t)+ ln C 得流线方程为 (x + t)(− y + t) = C 由上式可知，任一瞬时的流线是一双曲线

当t=0,x=-1,y=-1时，得到 xy=1 这就是1=0时刻，通过点A(L,-)的流线。它为一等变双曲线，在第三象限，如图34 所示。 图34 三、流管与流束 流管在流场中任取一非流线又不相交的封闭曲线，过曲线上各点作流线，这些流线组 成一个封闭的管状曲面，称为流管，如图35所示。由流线的定义可知，位于流管表面上得 流体质点只具有切于流管方向的速度，因而流体质点只能在流管内部或流管表面流动，而不 能穿越流管。流管如同真实的固体管壁，将其内部的流体限制在管内流动。自来水管的内表 面就是流管的一个实例。 图35所示 流束流管内的全部流体，称为流束。 微小的封闭曲线构成的流管内的流体称为元流，又称微元流束。元流的极限就是流线。 实际工程中，把管内流动和渠道中的流动看作是总的流束，它由无限多元流组成，称为 总流。 四、过流断面、湿周、水力半径、当量直径 过流断面与流束或总流的所有流线都相垂直的横断面称为过流断面。过流断面可能是平 面，也可能是各种形式的曲面，如图36所示。如果流体是水，称为过水断面。由于元流的 过流断面无限小，可以认为其断面上的运动参数分布均匀，但对于总流，过流断面上各点的 运动要素却不一定相等。 图3-6 湿周在总流的过流断面上，与流体相接触的周体边壁周长称为湿周，用x表示。 水力半径总流的过流断面面积与湿周的比值称为水力半径，用R表示。 R=4 当量直径总流过流断面面积的四倍与湿周的比值称为当量直径，用d。表示。 6

6 当 t = 0， x = −1， y = −1 时，得到 xy = 1 这就是 t = 0 时刻，通过点 A(-1,-1)的流线。它为一等变双曲线，在第三象限，如图 3-4 所示。 图 3-4 三、流管与流束 流管 在流场中任取一非流线又不相交的封闭曲线，过曲线上各点作流线，这些流线组 成一个封闭的管状曲面，称为流管，如图 3-5 所示。由流线的定义可知，位于流管表面上得 流体质点只具有切于流管方向的速度，因而流体质点只能在流管内部或流管表面流动，而不 能穿越流管。流管如同真实的固体管壁，将其内部的流体限制在管内流动。自来水管的内表 面就是流管的一个实例。 图 3-5 所示 流束 流管内的全部流体，称为流束。 微小的封闭曲线构成的流管内的流体称为元流，又称微元流束。元流的极限就是流线。 实际工程中，把管内流动和渠道中的流动看作是总的流束，它由无限多元流组成，称为 总流。 四、过流断面、湿周、水力半径、当量直径 过流断面 与流束或总流的所有流线都相垂直的横断面称为过流断面。过流断面可能是平 面，也可能是各种形式的曲面，如图 3-6 所示。如果流体是水，称为过水断面。由于元流的 过流断面无限小，可以认为其断面上的运动参数分布均匀，但对于总流，过流断面上各点的 运动要素却不一定相等。 图 3-6 湿周 在总流的过流断面上，与流体相接触的固体边壁周长称为湿周，用  表示。 水力半径 总流的过流断面面积与湿周的比值称为水力半径，用 R 表示。  A R = 当量直径 总流过流断面面积的四倍与湿周的比值称为当量直径，用 e d 表示。  A de 4 =

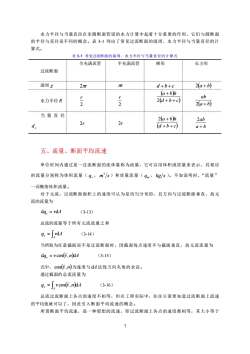
水力半轻与当量直径在非圆断面管道的水力计算中起若十分重要的作用，它们与圆断面 的半径与直径是不同的概念。表3列出了常见过流断面的湿周、水力半径与当量直径的计 算式。 表31常见过流断面的湿周、水力半径与当量直径的计算式 全充满流管 半充满流管 梯形 长方形 过流断面 湿周 2m d+b+c 2a+b) （a+bh ab 水力半径R r-2 2(d+b+c) 2(a+b) 当量直径 2r 2(a+b)h 2r 2ab (d+b+c) a+b 五、流量、断面平均流速 单位时间内通过某一过流断面的流体量称为流量，它可以用体积或质量米表示，其相应 的流量分别称为体积流量(q。,ms)和质量流量(q,kg小s)。不加说明时，“流量” ~词概指体积流量。 对于元流，过流断面面积上的速度可认为是均匀分布的，且方向与过流断面垂直，故元 流的流量为 dq,=vd4 (3-13) 总流的流量等于所有元流流量之和 9。=d4 (3-14) 当所取为任意截面而不是过流断面时，因截面每点速度不与藏截面垂直，故元流流量为 dq,vcos(v,ndA (3-15) 式中，cos(位，n)为速度与d4法线方向夹角的余弦。 通过截面的总流流量为 q.=vcos(v,n4 (3-16) 总流过流断面上各点的速度不相等，但在工程实际中，往往只需要知道过流断面上流速 的平均值就可以了，因此引入断面平均流速的概念。 所谓断面平均流速，是一种假想的流速，即过流断面上各点的速度都相等，其大小等于

7 水力半径与当量直径在非圆断面管道的水力计算中起着十分重要的作用，它们与圆断面 的半径与直径是不同的概念。表 3-1 列出了常见过流断面的湿周、水力半径与当量直径的计 算式。 表 3-1 常见过流断面的湿周、水力半径与当量直径的计算式 过流断面 全充满流管 半充满流管 梯形 长方形 湿周  2r r d +b + c 2(a + b) 水力半径 R 2 r 2 r ( ) (d b c) a b h + + + 2 (a b) ab 2 + 当量直径 e d 2r 2r ( ) (d b c) a b h + + 2 + a b ab + 2 五、流量、断面平均流速 单位时间内通过某一过流断面的流体量称为流量，它可以用体积或质量来表示，其相应 的流量分别称为体积流量（ v q ， m s 3 ）和质量流量（ m q ， kg s ）。不加说明时，“流量” 一词概指体积流量。 对于元流，过流断面面积上的速度可认为是均匀分布的，且方向与过流断面垂直，故元 流的流量为 dqv = vdA （3-13） 总流的流量等于所有元流流量之和  = A qv vdA （3-14） 当所取为任意截面而不是过流断面时，因截面每点速度不与截面垂直，故元流流量为 dqv v cos(v,n)dA  = （3-15） 式中， cos(v,n)  为速度与 dA 法线方向夹角的余弦。 通过截面的总流流量为 ( )  = A qv v cos v,n dA  （3-16） 总流过流断面上各点的速度不相等，但在工程实际中，往往只需要知道过流断面上流速 的平均值就可以了，因此引入断面平均流速的概念。 所谓断面平均流速，是一种假想的流速，即过流断面上各点的速度都相等，其大小等于

过流断面的流量q,除以过流断面面积A,即 v-2-Lu (3-17) 断面平均流速的概念十分重婴，它将使我们的研究和计算大为简化，尤其在工程计算中 具有重要的实际意义。 六、一元、二元、三元流动 根据决定流体运动参数所需的空间坐标的个数，可把流体流动分为一元流动、二元流动 和三元流动。实际流体力学问题，流动参数为三个坐标的函数，为三元流动。随着计算技术 的发展，对一些复杂问题的求解已成为可能，但对于大多数三元流动问题，研究分析通常十 分复杂。为此，在流体力学的研究和实际工程技术中，人们往往根据具体问题的性质把它简 化为二元甚至一元流动来处理。流动参数可表示为两个坐标的函数，称为二元流动。流动参 数只是一个空间坐标函数，称为一元流动。在工程流体力学中，经常引入断面平均流速的概 念，运用一元流动分析方法来解决管道与渠道中的很多流动问题。 七、均匀流动与非均匀流动 按各点运动要素（主要是速度）是否随位置而变化，可将流动分为均匀流动和非均匀流 动。流场中，在给定的某一时刻，各点速度都不随位置而变化的流动称为均匀流动。反之， 称为非均匀流动。均匀流动的所有流线都是平行直线，过流断面是一平面，且大小和形状都 沿程不变。非均匀流动的所有流线不是一组平行直线，过流断面不是一平面，且其大小或形 状沿程改变。例如，流体在等径长直管道内的流动，或在断面不变的长直渠道中的流动，都 是均匀流动。 均匀流动中，流动参数具有对空间的不变性，迁移加速度等于零。 八、渐变流与急变流 按流线沿程变化的缓急程度，又将非均匀流动分为渐变流与急变流。各流线接近于平行 直线的流动，称为渐变流。此时，各流线之间的夹角很小，且流线的曲率半径很大。反之， 称为急变流。由于渐变流的所有流线是一组几乎平行的直线，其过流断面可认为是一平面。 同时，恒定渐变流过流断面上东压强的分布近似地符合静压强的分布规律，即同一过流斯面 上：+卫÷常数。渐变流的极限情况就是均匀流。 直径沿程变化不大的圆锥管内的流动，可认为是渐变流。管径突然扩大或缩小处的流动， 可以认为是急变流。 8

8 过流断面的流量 v q 除以过流断面面积 A ，即 A vdA A q v v A = = （3-17） 断面平均流速的概念十分重要，它将使我们的研究和计算大为简化，尤其在工程计算中， 具有重要的实际意义。 六、一元、二元、三元流动 根据决定流体运动参数所需的空间坐标的个数，可把流体流动分为一元流动、二元流动 和三元流动。实际流体力学问题，流动参数为三个坐标的函数，为三元流动。随着计算技术 的发展，对一些复杂问题的求解已成为可能，但对于大多数三元流动问题，研究分析通常十 分复杂。为此，在流体力学的研究和实际工程技术中，人们往往根据具体问题的性质把它简 化为二元甚至一元流动来处理。流动参数可表示为两个坐标的函数，称为二元流动。流动参 数只是一个空间坐标函数，称为一元流动。在工程流体力学中，经常引入断面平均流速的概 念，运用一元流动分析方法来解决管道与渠道中的很多流动问题。 七、均匀流动与非均匀流动 按各点运动要素（主要是速度）是否随位置而变化，可将流动分为均匀流动和非均匀流 动。流场中，在给定的某一时刻，各点速度都不随位置而变化的流动称为均匀流动。反之， 称为非均匀流动。均匀流动的所有流线都是平行直线，过流断面是一平面，且大小和形状都 沿程不变。非均匀流动的所有流线不是一组平行直线，过流断面不是一平面，且其大小或形 状沿程改变。例如，流体在等径长直管道内的流动，或在断面不变的长直渠道中的流动，都 是均匀流动。 均匀流动中，流动参数具有对空间的不变性，迁移加速度等于零。 八、渐变流与急变流 按流线沿程变化的缓急程度，又将非均匀流动分为渐变流与急变流。各流线接近于平行 直线的流动，称为渐变流。此时，各流线之间的夹角很小，且流线的曲率半径很大。反之， 称为急变流。由于渐变流的所有流线是一组几乎平行的直线，其过流断面可认为是一平面。 同时，恒定渐变流过流断面上东压强的分布近似地符合静压强的分布规律，即同一过流断面 上 +  g p z  常数。渐变流的极限情况就是均匀流。 直径沿程变化不大的圆锥管内的流动，可认为是渐变流。管径突然扩大或缩小处的流动， 可以认为是急变流

第三节连续性方程 连续性方程是质量守恒定律在流体力学中的具体体现，实质上是质量守恒方程。 一、积分形式的连续性方程 在流场中取任意形状的一个控制体，如图37所示，设其体积为V,表面积为A,n为 微元面积外法线方向上的单位矢量。 图37 任何瞬时连续充清于控制体内的流体质量可以用微元质量的体积分表示为∬P业。 经过单位时间，如果控制体内的流体质量发生了变化，则单位时间内的变化量可表示为 会（P）.单位时同内，通进拉制面流入或流出拉制体的质甚之和为 f月，pvdA. 根据质量守恒定律，控制体内的质量发生变化的唯一原因就是经过控制面的流动，即单 位时间内控制体质量的变化量等于通过控制面流入或流出控制体的质量之和。也就是说，控 制体中质量的增加必然等于同一时间内流入与流出的质量差。反之，控制体中质量的减少必 然等于动一时间内流出于流入的质量差。因而有 f乐，pvdA=-84G 这就是积分形式的连续性方程。 二、微分形式的连续性方程 利用高斯定理，可将对面积的曲面积分，转化为三重体积分，即得 月pvdA=f,pm,dd止+pm,drd+pm.drd) -a()(ydz (319) y 根据控制体与时间无关的特性，可将合以，r先对控制体积分后对时间微分的次序 颠倒，则得 arfd ()-fdvddyd

9 第三节 连续性方程 连续性方程是质量守恒定律在流体力学中的具体体现，实质上是质量守恒方程。 一、积分形式的连续性方程 在流场中取任意形状的一个控制体，如图 3-7 所示，设其体积为 V ，表面积为 A ， n 为 微元面积外法线方向上的单位矢量。 图 3-7 任何瞬时连续充满于控制体内的流体质量可以用微元质量的体积分表示为 V dV 。 经过单位时间，如果控制体内的流体质量发生了变化，则单位时间内的变化量可表示为 ( )    V V t d 。 单 位 时 间 内 ， 通 过 控 制 面 流 入 或 流 出 控 制 体 的 质 量 之 和 为 A  v d A。 根据质量守恒定律，控制体内的质量发生变化的唯一原因就是经过控制面的流动，即单 位时间内控制体质量的变化量等于通过控制面流入或流出控制体的质量之和。也就是说，控 制体中质量的增加必然等于同一时间内流入与流出的质量差。反之，控制体中质量的减少必 然等于动一时间内流出于流入的质量差。因而有     = − A V A t  v d A d （3-18） 这就是积分形式的连续性方程。 二、微分形式的连续性方程 利用高斯定理，可将对面积的曲面积分，转化为三重体积分，即得 ( ) ( ) ( ) ( ) d dydz d d d d d d d            +   +   = = + + V x y z A x y z A x z v y v x v v A v y z v x z v x y        （3-19） 根据控制体与时间无关的特性，可将    V V t d 先对控制体积分后对时间微分的次序 颠倒，则得 d ( d ) d d dydz       =   =   =   V V V V x t V t V t V t    

(3-20) 将(319)和(3-20)代入积分形式的连续性方程式(318)，即得 ma）,）,g+器}ad-o Ox dv 由于积分区域为可以任意选取的控制体体积，积分为零则被积函数在流场中处处为零 「a,w,e]-0san y 这就是在直角坐标下的微分形式的连续性方程。 几种特殊情形下的连续性方程如下： 恒定流动，ap/0t=0,连续性方程简化为 apv,)dv,).)=0 (3-22) y 不可压缩流体，dp/d=0,连续性方程简化为 ++是=0 (3-22) 圆柱坐标系中的连续性方程的表达式为 ee vdo)don)dpv.)o (3-23) 三、恒定不可压缩总流的连续性方程 恒定不可压缩总流的连续性方程，可通过对总流控制体积分求得。在总流控制表面中 只有两个过流断面有流体通过，如图38所示。因为出口过流断面的面积矢量与速度矢量方 向一致，而进口的则相反，考虑恒定、不可压的特性，由式(3-18)可得 月ydA=JdA2-d4=可2A2-A=0 或2A2=1A=qr (3-24) 式中，4，A,分别为总流进、出口过流断面面积，可，分别为进、出口断面平均流 速。 图3-8 上式即为恒定不可压缩总流的连续性方程。它表明流体的体积流量沿程不变，对于任意 两过流断面，其断面平均流速与过流断面面积成反比

10 （3-20） 将（3-19）和（3-20）代入积分形式的连续性方程式（3-18），即得 ( ) ( ) ( ) d dydz = 0         +   +   +   V x y z x z t v y v x v    由于积分区域为可以任意选取的控制体体积，积分为零则被积函数在流场中处处为零， 得 ( ) ( ) ( ) = 0         +   +   +   z t v y v x v x  y  z  （3-21） 这就是在直角坐标下的微分形式的连续性方程。 几种特殊情形下的连续性方程如下： 恒定流动，  t = 0 ，连续性方程简化为 ( ) ( ) ( ) = 0   +   +   z v y v x vx y  z   （3-22） 不可压缩流体， d dt = 0 ，连续性方程简化为 = 0   +   +   z v y v x vx y z （3-22） 圆柱坐标系中的连续性方程的表达式为 ( ) ( ) ( ) 0 1 1 =   +   +   + +   z v v r r v r r v t r r  z       （3-23） 三、恒定不可压缩总流的连续性方程 恒定不可压缩总流的连续性方程，可通过对总流控制体积分求得。在总流控制表面中， 只有两个过流断面有流体通过，如图 3-8 所示。因为出口过流断面的面积矢量与速度矢量方 向一致，而进口的则相反，考虑恒定、不可压的特性，由式（3-18）可得 d 2 d 2 1 d 1 2 2 1 1 0 2 1 = − = − =    v A v A v A v A v A A A A 或 A qV v2 A2 = v1 1 = （3-24） 式中， A1， A2 分别为总流进、出口过流断面面积， 1 v ， 2 v 分别为进、出口断面平均流 速。 图 3-8 上式即为恒定不可压缩总流的连续性方程。它表明流体的体积流量沿程不变，对于任意 两过流断面，其断面平均流速与过流断面面积成反比