《流体力学》课程教学课件（PPT讲稿）第三章 流体动力学基础 Fluid Dynamics

第三章 流体动力学基出 Fluid Dynamics 1

1 第三章 流体动力学基础 Fluid Dynamics

Fluid Dynamics 流体动力学主要研究流体处于运动状态时的力 学规律，以及这些规律在实际工程中的应用。 本章主要内容： 3-1流体运动的描述 3-2流体运动的基本概念 3-3连续方程式 3-4纳维-斯托克斯方程式 3-5伯努利方程式及其应用 2

2 Fluid Dynamics 本章主要内容： 3-1 流体运动的描述 3-2 流体运动的基本概念 3-3 连续方程式 3-4 纳维-斯托克斯方程式 3-5 伯努利方程式及其应用 流体动力学主要研究流体处于运动状态时的力 学规律，以及这些规律在实际工程中的应用

3-1流体运动的描述 描述流体运动就是表达流动参数在空间不同位置上随时 间连续变化的规律。 流动参数：表征流体运动的主要物理量统称为流体的流 动参数。包括：流动速度V、压力P、位移(XY,z)、密度、 动量、动能等。 描述流体运动是从着眼于研究流体质点的运动，还是着 眼于研究流场空间点上流动参数的变化出发，可分为： 拉格朗日(Lagrange)法和欧拉(Euler)法。 3

3 描述流体运动就是表达流动参数在空间不同位置上随时 间连续变化的规律。 流动参数：表征流体运动的主要物理量统称为流体的流 动参数。包括：流动速度V、压力P 、位移(x,y,z)、密度、 动量、动能等。 描述流体运动是从着眼于研究流体质点的运动，还是着 眼于研究流场空间点上流动参数的变化出发，可分为： 拉格朗日（Lagrange）法和欧拉（Euler）法。 3-1 流体运动的描述

3-1流体运动的描述 拉格朗日法与质点系 跟踪流体质点的运动全过程并描述运动过程中各质点、 各物理量随时间变化的规律的方法称为拉格朗日法。 设t=t时，流体质点的坐标值是(a,b,c) 流体质点的运动坐标(xy,Z) x-x(a,b,c,t) y-y(a,b,c,t) z-z(a,b,c,t) a,b,C,t—拉格朗日变数 4

4 一 拉格朗日法与质点系 跟踪流体质点的运动全过程并描述运动过程中各质点、 各物理量随时间变化的规律的方法称为拉格朗日法。 设t=t0时,流体质点的坐标值是（a, b, c） 流体质点的运动坐标（x, y, z） x=x(a,b,c,t) y=y(a,b,c,t) z=z(a,b,c,t) a, b, c, t——拉格朗日变数 3-1 流体运动的描述

3-1流体运动的描述 表3一！用拉格朗日法描述流体运动的表达式 质点运动坐标 质点速度 质点加速度 x=x(a.b,c,t) =4=v(a,b,c,1) ar=ddv. dt2 dt =az(a,b,c.1) y=y(a,b,c,t） w==(a,b,c,) dt =ay(a,b,c,:) 之=z(a,b,c,t】 =bz(a,b,c,l） a乐-船 dt -a:(a,b,c,1) 质点系：由具有不同起始坐标的无数质点组成的具有一定流动参 数的物质实体称为质点系。 在流动过程中，质点系的位置、形状和流动参数都可能发生变化。 5

5 3-1 流体运动的描述 质点系：由具有不同起始坐标的无数质点组成的具有一定流动参 数的物质实体称为质点系。 在流动过程中，质点系的位置、形状和流动参数都可能发生变化

3-1流体运动的描述 二 欧拉法与控制体 以数学场论为基础，着眼于任何时刻物理量在场上的 分布规律的流体运动描述方法称为欧拉法。 流体质点速度V、压力p、密度p和温度T等的表达式为： vx=vx(x,y,=,t)=vx[x(t),y(t),z(t),t] w=(x,y,2,t)=v[x(t)y(t),z(t),t] =v(x,y,2,t)=v:[x(t),y(t),z(t),t] p=p(x,y,z,t) p=p(x,y,z,1) T=T(x,y,z,t) 其中x,y,2,t为欧拉变数 6

6 二 欧拉法与控制体 以数学场论为基础，着眼于任何时刻物理量在场上的 分布规律的流体运动描述方法称为欧拉法。 3-1 流体运动的描述 流体质点速度v、压力p、密度ρ和温度T等的表达式为：     v v x y z t v x t y t z t t v v x y z t v x t y t z t t v v x y z t v x t y t z t t z z z y y y x x x ( , , , ) ( ), ( ), ( ), ( , , , ) ( ), ( ), ( ), ( , , , ) ( ), ( ), ( ), = = = = = = ( , , , ) ( , , , ) ( , , , ) T T x y z t x y z t p p x y z t = = =   其中 x, y,z,t 为欧拉变数

3-1流体运动的描述 控制体：研究流体运动的连续的空间区域称为控制体。 相对于坐标系有固定位置、有任意确定形状的空间区域，控制 体的表面也称为控制面，流体质点系可以按照自身运动规律穿越 控制面自由出入于控制体。 控制体与质点系的区别： 质点系相对于坐标系不但可以有位移，而且也可以有变形；但 对于控制体，在运动过程中相对于坐标系的位置与形状都是固定 不变的。 7

7 3-1 流体运动的描述 控制体:研究流体运动的连续的空间区域称为控制体。 相对于坐标系有固定位置、有任意确定形状的空间区域，控制 体的表面也称为控制面，流体质点系可以按照自身运动规律穿越 控制面自由出入于控制体。 控制体与质点系的区别： 质点系相对于坐标系不但可以有位移，而且也可以有变形；但 对于控制体，在运动过程中相对于坐标系的位置与形状都是固定 不变的

3-1流体运动的描述 三 流场的两个特例 1定常场 流场中的速度、压强、密度、温度等物理量的分布与时间无关， 则称为定常场（定常流动)。 m_0p_p_0r==0 atatat at 2均匀场 流场中的速度、压强、密度、温度等物理量的分布与空间坐标无 关，则称为均匀场（均匀流动）。 Ov 0v_0v_op_8p_Op=.-0 ax ay Oz Ox ay Oz 8

8 三 流场的两个特例 3-1 流体运动的描述 1 定常场 流场中的速度、压强、密度、温度等物理量的分布与时间无关， 则称为定常场（定常流动）。 = . = 0   =   =   =   t T t t p t v  2 均匀场 流场中的速度、压强、密度、温度等物理量的分布与空间坐标无 关，则称为均匀场（均匀流动）。 = . = 0   =   =   =   =   =   z p y p x p z v y v x v

3-2流体运动的基本概念 物理量的质点导数 运动中的流体质点所具有的物理量N(速度、压强、密度、质量、 温度、动量、动能等)对时间的变化率称为物理量的质点导数。 dN △W =lim dt △t 2 dN ON aNaN ON =1以 M(E+△)D dt Ox △5B(x+△x,y+Ay,z+△x) dN aN M(A(y) =(v.V)N+ y dt 8t 当地导数 迁移导数 哈密顿算子 9

9 lim dN N dt t  =  3-2 流体运动的基本概念 运动中的流体质点所具有的物理量N(速度、压强、密度、质量、 温度、动量、动能等)对时间的变化率称为物理量N的质点导数。 一 物理量的质点导数 t N N dt dN   = (v ) + t N z N v y N v x N v dt dN y z x   +   +   +   = x y z  +   +    = i j k 哈密顿算子 当地导数 迁移导数

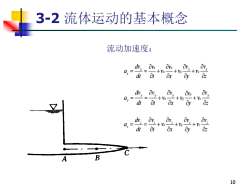
3-2流体运动的基本概念 流动加速度： 血=+a+w+ 0= -+ -+ dt otox + a.= dt ot ox”yaz A B 10

10 3-2 流体运动的基本概念 流动加速度： x x x x x x y z x dv v v v v a v v v dt t x y z     = = + + +     y y y y y x y z y dv v v v v a v v v dt t x y z     = = + + +     z z z z z x y z z dv v v v v a v v v dt t x y z     = = + + +    