北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第7章 多元函数微分及其应用 第5节 方向导数与梯度

第5节 第七章 方向导数与梯度 一、方向导数 二、梯度 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页 返回 结束
目录 上页 下页 返回 结束 第七章 第5节 一、方向导数 二、梯度 方向导数与梯度

一、方向导数 定义1若函数f(x,y)在点P(x,y)处 沿方向1(方向角为α,B)存在下列极限: P(x,y) lim △f x p>0 0 lim f(x+△x,y+△y)-f(x,y)记作∂f p-→0 al 】 则称⊙f 为函数在点P处沿方向1的方向导数 al BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束
目录 上页 下页 返回 结束 一、方向导数 定义1 若函数 f (x, y) f 0 lim 则称 l f l f ( ) ( ) , 2 2 x y x cos , y cos 为函数在点 P 处沿方向 l 的方向导数. ( , ) ( , ) lim 0 f x x y y f x y 在点P(x, y) 处 沿方向 l (方向角为 , ) 存在下列极限: 记作 P(x, y) l x y O ' P

定理若函数f(x,y)在点P(x,y)处可微, 则函数在该点沿任一方向1的方向导数存在,且有 B1=Ofcosa+ fcosB. 其中a,B为l的方向角 P(x,y) 证明:由函数f(x,y)在点P可微,得 Aj=IAx+I△ytop) 8x 0y =p(wa一影as))-olp) 故 of lim Af =2f cosa+ of cosB al p-→0 8x BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束
目录 上页 下页 返回 结束 定理 若函数 f (x, y) 在点 P(x, y) 处可微 , 则函数在该点沿任一方向 l 的方向导数存在 , f l f 0 lim cos cos , y f x f l f 其中 , 为l的方向角. 证明: 由函数 f (x, y) y o ( ) y f x x f f cos cos y f x f 且有 o( ) 在点 P 可微 , 得 故 cos cos y f x f P(x, y) l x y O ' P

特别: ·当/与x轴同向a=0,B=)时,有 of af al 8x ·当1与x轴反向(a=不,B=乃时,有 of of al 8x 对于三元函数f(x,y,)在点P(x,y,z)处可微分,则 of lim f(x+△x,y+△y,2+△)-f(x,y,2) al p→0 of osa+0Lcosg+ cos y x 0y 0z P=(A)2+(A)2+(A=2, Ax=pcosa,△y=PcoS阝,A2=pcosy BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上页 下页 返回 结束
目录 上页 下页 返回 结束 x f l f 特别: • 当 l 与 x 轴同向 时,有 2 0, α β • 当 l 与 x 轴反向 时,有 2 , α β x f l f 对于三元函数 f (x, y,z) 在点 P(x, y,z) 处可微分,则 ( , , ) ( , , ) lim 0 f x x y y z z f x y z l f cos cos cos z f y f x f ( ) ( ) ( ) , 2 2 2 x y z x cos , y cos , z cos

例7.5.1求函数z=x2+y在点2,1)处沿方向1=37-47 的方向导数 解:向量1的方向余弦为 3 4 cosa= 5 cosA=- 5 =2x =4, =2y =2, @x (2,1 (2,1) y2, (2,1) 故在点(2,1)处,所求方向导数 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束
目录 上页 下页 返回 结束 例7.5.1 求函数z x 2 y 2在点 (2, 1) 处沿方向l 3i 4 j 的方向导数 . , 5 3 cos 2 4, (2,1) (2,1) x x z , 5 4 cos 解: 向量 l 的方向余弦为 2 2, (2,1) (2,1) y y z 故在点 (2, 1) 处,所求方向导数 . 5 4 5 4 2 5 3 4 l z

二、梯度 定义2设函数z=x,y)在点x,y)的某邻域内具 有一阶连续偏导数 1⊙,则向量 Ox oy 8I+ ∂x 称为函数z=x,y)在点(x,y)的梯度,记作gradfx, ),即 gradf() 影 0x BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束
目录 上页 下页 返回 结束 二、梯度 定义2 设函数z=f(x,y)在点(x,y)的某邻域内具 有一阶连续偏导数 ,则向量 y f x f , j y f i x f 称为函数z=f(x,y)在点(x,y)的梯度,记作gradf(x, y),即 j y f i x f f x y grad ( , )

(1)当0=0时, 达到最大,最大值是 gradf(x,y) 即方向与梯度的方向一致时,方向导数取到最大 值.梯度的方向是函数x,y)在点(x,y)增长最快 的方向 (2)当0=π时, 亲到最小,最小值是 -gradf(x,y). 即负梯度的方向是函数x,y)在点(x,y)减少最快 的方向 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束
目录 上页 下页 返回 结束 (1)当θ=0时, 达到最大,最大值是 | ( , ) | . 2 2 y f x f gradf x y | gradf (x, y) | . l f 即方向l与梯度的方向一致时,方向导数取到最大 值.梯度的方向是函数f(x,y)在点(x,y)增长最快 的方向. (2)当θ=π时, 达到最小,最小值是 l f 即负梯度的方向是函数f(x,y)在点(x,y)减少最快 的方向.

梯度的几何意义 对函数:=f(x,),曲线 任》在0面1的设影 D:f(x,y)=c称为函数f的等值线或等高线.举例 设fx,才,不同时为零, 则L*上点P处的法向量为 (fs,fy)p=gradf p =Vfp 函数在一点的梯度垂直于该点等值线! 指向函数增大的方向 同样,f(x,y,z)=c称为u=f(x,y,z) 的等值面(等量面).当其各偏导数不同 (设c,<C2) 时为零时,其上点P处的法向量为gradfp=Vfp BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束
目录 上页 下页 返回 结束 梯度的几何意义 O y x 1 f c f c ( ) 1 2 设c c P 曲线 在 xOy 面上的投影 z c z f x y ( , ) L : f (x, y) c * 称为函数 f 的等值线或等高线 . 设 , 不同时为零 , x y f f 则L*上点P 处的法向量为 x y P ( f , f ) P grad f 2 f c 对函数 z f (x, y), 举例 函数在一点的梯度垂直于该点等值线, 指向函数增大的方向. 同样, u f (x, y,z) 的等值面(等量面). f (x, y,z) c 当其各偏导数不同 其上点 P 处的法向量为 P grad f 称为 时为零时, P f . P f
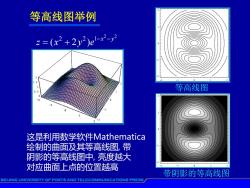
等高线图举例 2=(x2+2y2)e-2-y 等高线图 这是利用数学软件Mathematica 急 绘制的曲面及其等高线图,带 阴影的等高线图中,亮度越大 -2 对应曲面上点的位置越高 -2 2 带阴影的等高线图 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS
等高线图举例 -2 -1 0 1 2 -2 -1 0 1 2 0 0.5 1 1.5 2 -2 -1 0 1 2 -2 -1 0 1 2 -2 -1 0 1 2 2 2 2 2 1 ( 2 ) x y z x y e -2 -1 0 1 2 -2 -1 0 1 2 这是利用数学软件Mathematica 绘制的曲面及其等高线图, 带 阴影的等高线图中, 亮度越大 对应曲面上点的位置越高 等高线图 带阴影的等高线图

例7.5.3求梯度向量grad x2+y2 解自于x刀求架 2x of 2y ax (x2+y>(x2+y2 grad 2× 2y BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束
目录 上页 下页 返回 结束 例7.5.3 求梯度向量 解: 由于 , ( ) 2 , ( ) 2 2 2 2 2 2 2 x y y y f x y x x f . 1 2 2 x y grad ,求得 1 ( , ) 2 2 x y f x y . ( ) 2 ( ) 1 2 2 2 2 2 2 2 2 2 j x y y i x y x x y grad
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第7章 多元函数微分及其应用 第4节 复合函数与隐函数求导法.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第7章 多元函数微分及其应用 第3节 全微分及其应用.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第7章 多元函数微分及其应用 第2节 偏导数.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第7章 多元函数微分及其应用 第1节 多元函数的基本概念与极限.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第6章 空间解析几何 第6节 空间曲线及其方程.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第6章 空间解析几何 第5节 曲面及其方程.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第6章 空间解析几何 第4节 空间直线及其方程.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第6章 空间解析几何 第3节 平面及其方程.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第6章 空间解析几何 第2节 向量的向量积.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第6章 空间解析几何 第1节 预备知识.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第5章 定积分 第7节 定积分的物理应用.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第5章 定积分 第6节 定积分在几何学上的应用.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第5章 定积分 第5节 广义积分.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第5章 定积分 第4节 定积分的换元积分法和分部积分法.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第5章 定积分 第3节 微积分基本公式.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第5章 定积分 第2节 定积分的基本性质.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第5章 定积分 第1节 定积分的概念.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第4章 不定积分 第5节 有理函数和可化为有理函数的积分.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第4章 不定积分 第4节 分部积分法.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第4章 不定积分 第3节 第二类换元积分法.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第7章 多元函数微分及其应用 第6节 微分法在几何上的应用.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第7章 多元函数微分及其应用 第7节 多元函数的极值及其求法.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第8章 重积分 第1节 二重积分的概念与性质.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第8章 重积分 第2节 二重积分的计算.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第8章 重积分 第3节 二重积分的应用.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第8章 重积分 第4节 三重积分的概念及计算.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第1节 对弧长的曲线积分.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第2节 对坐标的曲线积分.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第3节 格林公式及其应用.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第4节 对面积的曲面积分.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第5节 对坐标的曲面积分.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第6节 高斯公式与斯托克斯公式.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第10章 无穷级数 第1节 常数项级数的概念和性质.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第10章 无穷级数 第2节 常数项级数的审敛法.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第10章 无穷级数 第3节 幂级数.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第10章 无穷级数 第4节 函数展开成幂级数.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第10章 无穷级数 第5节 傅里叶级数.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第11章 微分方程 第1节 微分方程的基本概念.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第11章 微分方程 第2节 一阶微分方程的解法.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第11章 微分方程 第3节 高阶微分方程的解法.pdf
