北京邮电大学出版社：21世纪高等学校规划教材《高等数学》课程教学资源（课件讲稿）第10章 无穷级数 第1节 常数项级数的概念和性质

第7为 第十章 常数项级数的橇念和性质 常数项级数的概念 二、收敛级数的基本性质 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束

目录 上页 下页 返回 结束 常数项级数的概念和性质 一、常数项级数的概念 二、收敛级数的基本性质 第1节 第十章

一、常数项级数的概念 引例圆的面积问题 依次作圆内接正3×2”(n=1,2,…)边形，设a1表示 内接正六边形面积，a表示边数增加 时增加的面积，如此继续进行n次， Sn=a1+a2+…+am n→o时，这个和越近似于圆的面积S 即 S limS,lim(a +a2 +..+a,) n→o0 n→o0 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页 返回结束

目录 上页 下页 返回 结束 一、常数项级数的概念 引例 圆的面积问题. 依次作圆内接正 边形, 这个和越近似于圆的面积 S . 设 a1 表示 即 内接正六边形面积, ak 表示边数增加 时增加的面积,如此继续进行n次

定义1设给定一个数列41,42，，…，4n,…将各项依 次相加，简记为∑4n,即 n=l 00 ∑24n=4+42+4+…+4n十 n=1 称上式为无穷级数，其中第n项n称为级数的一般项。 级数的前n项和 s。=∑4，=41+42+43++47 i 称为级数的部分和 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束

目录 上页 下页 返回 结束 定义1 设给定一个数列 u1 , u2 , u3 ,  , un ,  将各项依 , 1   n n u 即 称上式为无穷级数，其中第 n 项 n u 称为级数的一般项, 级数的前 n 项和 称为级数的部分和. 次相加, 简记为

定义2如果级数∑u,的部分和数列{sn}有极限s,即 n= lim s =S n→oo 则称无穷级数收敛，s称为级数的和，记作 S=∑4n=4十2+…+4n+ n= 如果{S}没有极限，则称无穷级数发散，这时级数没 有和. 当级数收敛时，其部分和s是级数和s的近似值，称 Tn=S一Sn=弘n+1十4n2十…十4n+k十为级数∑4，的 余项 1n= BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 返回 结束

目录 上页 下页 返回 结束 如果{sn }没有极限，则称无穷级数发散，这时级数没 有和． 当级数收敛时，其部分和sn是级数和s的近似值，称 rn ＝s－sn ＝un+1＋un+2＋…＋un＋k＋…为级数 的 余项． 则称无穷级数收敛， s称为级数的和，记作 如果级数 的部分和数列{sn 定义2 }有极限s，即

例10.1.3讨论公比为g的等比级数（又称几何级数） ∑ag”=a+aq+ag2+…+ag”+…(a≠0) n=0 的敛散性 解：若g≠1，则部分和 Sn=a+aq+ag2+…+ag-la-ag” 1-q 当g00 等比级数收敛，其和为”g 当q>1时，由于1imq”=o,因而lims.=o, n 1n→o0 n->oo 这时等比级数发散 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束

目录 上页 下页 返回 结束 例10.1.3 讨论公比为q 的等比级数 (又称几何级数) 的敛散性. 解: 若 q a a q n    1 因而 1 lim a n q n s    等比级数收敛 , ; 1 q a  因而 lim , n n s    则部分和 这时等比级数发散 . 其和为

若9=1，则 当q=1时，Sn=na-→o,因此等比级数发散； 当q=-1时，级数成为 a-a+a-a+…+(-1)2-a+… n为奇数 因此 n为偶数 从而lims不存在，这时等比级数发散， n=>o0 综合可知， q<1时，等比级数收敛； q21时，等比级数发散 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上页 下页 返回 结束

目录 上页 下页 返回 结束 若 因此等比级数发散 ; 因此 n s     n 为奇数 n 为偶数 从而 综合可知, q 1 时, 等比级数收敛 ; q 1时, 等比级数发散 . 则 级数成为 a, 0, 不存在 , 这时等比级数发散

二、收敛级数的基本性质 性质1如果级数 ∑4n收敛于和s,即s=∑un,则各项 n=] n= 乘以常数k所得级数∑k4n也收敛，其和为s. n=】 证：令sn=∑4n，则o。=∑k4n=kSn, n= n= lim n=k lims,=ks n→oo n-→o0 这说明 ∑kn收敛，且和为s. n=1] 说明：级数的每一项同乘一个非零常数后，它的敛 散性不会改变 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束

目录 上页 下页 返回 结束 二、收敛级数的基本性质 性质1 如果级数 收敛于和 s , 1 , n n s u     则各项 乘以常数 k 所得级数 也收敛 , 证: 令 1 , n n n s u     则 1 n n n  k u     , n  k s n n    lim  ks 这说明 1 n n k u    收敛 , 且和为 ks . 说明: 级数的每一项同乘一个非零常数后，它的敛 散性不会改变. 即 其和为 ks

性质2设有两个收敛级数 s=∑4，=∑n n=l n=l 则级数 ∑(4n土vn必收敛，且其和为s士O, n=] 证：令n=∑4n,o,=∑n,则 n= n=∑(4，±)=Sn士o,→s±a(n→o) n= 这说明级数∑(4n±yn)也收敛，其和为s±O. n=1 说明：两个收敛级数逐项相加（相减）所得级数仍收敛， BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 下页 返回 结束

目录 上页 下页 返回 结束 性质2 设有两个收敛级数 1 , n n s u         n 1 n  v 则级数 ( ) 1 n n n  u  v   必收敛, 且其和为 s  . 证: 令 1 , n n n s u     1 , n n n  v     则 1 ( ) n n n n  u v          s n  ( ) 这说明级数 ( ) 1 n n n  u  v   也收敛, 其和为 s  . 说明：两个收敛级数逐项相加(相减)所得级数仍收敛．

性质3在级数中去掉、加上或改变有限项，不改变 级数的敛散性 证：将级数∑u的前k项去掉，所得新级数 ∑4k+n n=l n=1 的部分和为 7n=∑4k1=Skn-S 由于n→o时，O,与Sn极限状况相同，故新旧两级 数敛散性相同 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页 返回结束

目录 上页 下页 返回 结束 性质3 在级数中去掉、加上或改变有限项, 不改变 级数的敛散性. 证: 将级数   n1 n u 的前 k 项去掉, 的部分和为     n l n k l u 1  k n k s s    数敛散性相同. 极限状况相同, 故新旧两级 所得新级数

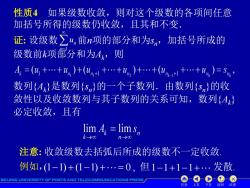
性质4如果级数收敛，则对这个级数的各项间任意 加括号所得的级数仍收敛，且其和不变 证：设级数∑4n前n项的部分和为sn,加括号所成的 级数前项都分和为A,则 A=(4+…+4）+(u+1十…+）+…+（十…+）=Sn 数列{A}是数列{sn}的一个子数列.由数列{sn}的收 敛性以及收敛数列与其子数列的关系可知，数列{A} 必定收敛，且有 lim 4 lim s 注意：收敛级数去括弧后所成的级数不一定收敛 例如，(1-1)+(1-1)+…=0，但1-1+1-1+…发散 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 返回 结束

目录 上页 下页 返回 结束 性质4 如果级数收敛，则对这个级数的各项间任意 加括号所得的级数仍收敛，且其和不变． 证: 设级数 前n项的部分和为sn，加括号所成的 级数前k项部分和为Ak，则 1 n n u    注意: 收敛级数去括弧后所成的级数不一定收敛. 例如，(11)  (11)  0 , 但 发散. 数列{Ak }是数列{sn }的一个子数列．由数列{sn }的收 敛性以及收敛数列与其子数列的关系可知，数列{Ak } 必定收敛，且有