银川能源学院:《概率论与数理统计》课程教学资源(PPT课件讲稿)第三章 多维随机变量

概率论与数理统道 第三章 多维随机变量 第一节 二维随机变量及其分布 第二节 边缘分布 第三节 条件分布 第四节 随机变量的独立性 第五节 两个随机变量函数的分布
第三章 多维随机变量 第一节 二维随机变量及其分布 第二节 边缘分布 第三节 条件分布 第四节 随机变量的独立性 第五节 两个随机变量函数的分布

概率论与数理统计 第一节 二维随机变量及其分布 1、二维随机变量的定义及其分布函数 定义3.1设E是一个随机试验,它的样本空间是 2={e}.设X(e)与Y(e)是定义在同一样本空间2上的两 个随机变量,则称X(e,Y(e)为2上的二维随机变量或 二维随机向量。简记为X,) 定义3.2设(X,)是二维随机变量,对于任意实数xy,称 二元函数 Fx,y)=P{X≤x,Y} 为二维随机向量(X,)的分布函数或联合分布函数。 上一页 一页 返回
上一页 下一页 返回 1、二维随机变量的定义及其分布函数 定义3.1 设E是一个随机试验,它的样本空间是 ={e}.设X(e)与Y(e)是定义在同一样本空间上的两 个随机变量,则称(X(e),Y(e))为上的二维随机变量或 二维随机向量。简记为(X,Y). 定义3.2 设(X,Y)是二维随机变量,对于任意实数x,y,称 二元函数 F(x,y)=P{Xx,Yy} 为二维随机向量(X,Y)的分布函数或联合分布函数。 第一节 二维随机变量及其分布
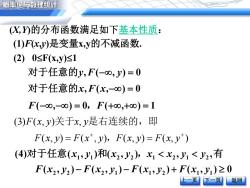
概率论与数理统计 X,)的分布函数满足如下基本性质: (1)Fxy)是变量x,y的不减函数. (2)0≤F(x,y)≤1 对于任意的y,F(-o0,y)=0 对于任意的x,F(x,-o)=0 F(-0,-00)=0,F(+o0,十0)=1 (3)F(x,y)关于x,y是右连续的,即 F(x,y)=F(x",y),F(x,y)=F(x,y*) (4)对于任意(x1,y1)和(x2Jy2),1<2,y1<y2,有 F(x2,y2)-F(x2,y1)-F(x1,y2)+F(x1,y1)≥0 上一页下一页 返回
上一页 下一页 返回 (X,Y)的分布函数满足如下基本性质: (2) 0F(x,y)1 (1)F(x,y)是变量x,y的不减函数. 对于任意的y,F(, y) 0 对于任意的x,F(x,) 0 F(,) 0,F(,) 1 (3) ( , ) , ( , ) ( , ) ( , ) ( , ) F x y x y F x y F x y F x y F x y 关于 是右连续的,即 , ( , ) ( , ) ( , ) ( , ) 0 (4) ( , ) ( , ) , , 2 2 2 1 1 2 1 1 1 1 2 2 1 2 1 2 F x y F x y F x y F x y 对于任意 x y 和 x y ,x x y y 有

概率论与数理统计 2、二维离散型随机变量 定义3.3若二维随机向量(X,)的所有可能取值是有 限对或无限可列多对,则称(X,Y)为二维离散型随机 变量。 设(X,)的一切可能值为(cy),=1,2,…,且(X,)取 各对可能值的概率为 P=x;,Yypij,ij=1,2,... (1)非负性:p20,i,j-1,2. (2)规范性:∑P;=1 上一页 下一页 返回 i,j
上一页 下一页 返回 2、二维离散型随机变量 定义3.3 若二维随机向量(X,Y)的所有可能取值是有 限对或无限可列多对,则称(X,Y) 为二维离散型随机 变量。 设(X,Y)的一切可能值为(xi,yj),i,j=1,2,… ,且(X,Y)取 各对可能值的概率为 P{X=xi,Y=yj}=pij, i,j=1,2,… (1) 非负性: pij≥0,i,j=1,2…; (2) 1 , i j ij 规范性: p

概率论与数理统计 离散型随机变量X,Y的联合分布函数 )-PX7川是点, 例3.2 设随机变量X在1,2,3,4四个整数中等可能 地取值,另一个随机变量Y在1~X中等可能地取一整 数值,试求(X,Y)的分布律. 解由乘法公式容易求得(X,Y)的分布律,易知 X=i,Y=}的取值情况是:=1,2,3,4,取不大于 的正整数,且 上一页 下一页 返回
上一页 下一页 返回 , ( , ) { , } X Y F x y P X x Y y p ij x x y y i i 离散型随机变量 的联合分布函数 例3.2 设随机变量X在1,2,3,4四个整数中等可能 地取值,另一个随机变量Y在1~X中等可能地取一整 数值,试求(X,Y)的分布律. 解 由乘法公式容易求得(X,Y)的分布律,易知 {X=i,Y=j}的取值情况是:i=1,2,3,4,j取不大于 i的正整数,且

概率论与数理统计 P(X-iY-A-P(Y-jlX-0P(X--a 1 i=1,2,3,4,j≤i. 于是(X,Y)的分布律如下表 XK 1 2 3 4 1 1/4 1/8 1/12 1/16 2 0 1/8 1/12 1/16 3 0 0 1/12 1/16 4 0 0 0 1/16 上一页 下一页 返回
上一页 下一页 返回 于是(X,Y)的分布律如下表 1 1 , | , 4 1,2,3,4, . P X i Y j P Y j X i P X i i i j i XY 1 2 3 4 1 2 3 4 1/4 1/8 1/12 1/16 0 1/8 1/12 1/16 0 0 1/12 1/16 0 0 0 1/16

概率论与数理统计 3、二维连续型随机变量 定义3.4 设(X,)为二维随机向量,X,)的分布函数为 Fc,y).若存在非负二元函数fx,y),对于任意实数xy,有 F(x,Jy)=∫nf(u,v)dd 则侧称(X,Y)为二维连续型随机向量. 非负二元函数f(x,y)称为(X,Y)的 联合概率密度函数,简称为概率密度. 上一页 下一页 返回
上一页 下一页 返回 3 、二维连续型随机变量 , . ( , ) ( , ) 联合概率密度函数 简称为概率密度 非负二元函数 f x y 称为 X Y 的 定义3.4 设(X,Y)为二维随机向量,(X,Y)的分布函数为 F(x,y).若存在非负二元函数f(x,y),对于任意实数x,y,有 x y F ( x, y) f (u, v)dvdu 则称(X,Y )为二维连续型随机向量

概率论与数理统计 概率密度f(x,y)的性质: (1)f(x,y)≥0; (2)["f(u,v)dudy =1 (3)若f(x,y)在(x,y)连续,则 O2F(x,y)=f(x,y) Oxoy (4)设G为xOy平面的一区域,则 P(X,Y)∈G}=Jj丁f(x,y) 上一页 下一页 返回
上一页 下一页 返回 (2) f (u, v)dudv 1 概率密度f ( x, y)的性质: (1) f ( x, y) 0; ( , ) ( , ) (3) ( , ) ( , ) , 2 f x y x y F x y f x y x y 若 在 连续 则 G P X Y G f x y dxdy G xOy {( , ) } ( , ) (4)设 为 平面的一区域 ,则

概率论与数理统计 在几何上z=f(x,y)表示空间的一张曲面. 由性质(2)知, 介于该曲面和xOy平面之间空间区域的体积为1, 由性质(4)知,P{(X,Y)∈D的值等于以G为底, 以曲面z=f(x,y)为顶的曲顶柱体的体积. 上一页 下一页 返回
上一页 下一页 返回 ( , ) . (4) , {( , ) } , 1, (2) , ( , ) . 以曲面 为顶的曲顶柱体的体积 由性质 知 的值等于以 为底 介于该曲面和 平面之间空间区域的体积为 由性质 知 在几何上 表示空间的一张曲面 z f x y P X Y D G xOy z f x y

概率论与数理统计 二维均匀分布 设G是平面上的有界区域,其面积为S,若二维随机变 量(X.,Y)的概率密度为 (x,y)∈G 10 其它 则称X,Y)在区域G上服从均匀分布. 设(X,Y)在区域G上服从均匀分布,D为G内的一区域,即 DcG,且D的面积为SD),那么 PX,)eD-=∬=∬5-S智 S(D) 上一页 下一页 返回
上一页 下一页 返回 设G是平面上的有界区域,其面积为S,若二维随机变 量(X.,Y)的概率密度为 0 其它 ( , ) 1 ( , ) x y G f x y A 设(X,Y)在区域G上服从均匀分布,D为G内的一区域,即 DG,且D的面积为S(D),那么 S S D dxdy S P X Y D f x y dxdy D D 1 ( ) {( , ) ) ( , ) 二维均匀分布 则称(X,Y)在区域G上服从均匀分布
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 银川能源学院:《概率论与数理统计》课程教学资源(PPT课件讲稿)第一章 概率论的基本概念.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第11章 微分方程 第3节 高阶微分方程的解法.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第11章 微分方程 第2节 一阶微分方程的解法.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第11章 微分方程 第1节 微分方程的基本概念.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第10章 无穷级数 第5节 傅里叶级数.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第10章 无穷级数 第4节 函数展开成幂级数.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第10章 无穷级数 第3节 幂级数.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第10章 无穷级数 第2节 常数项级数的审敛法.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第10章 无穷级数 第1节 常数项级数的概念和性质.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第6节 高斯公式与斯托克斯公式.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第5节 对坐标的曲面积分.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第4节 对面积的曲面积分.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第3节 格林公式及其应用.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第2节 对坐标的曲线积分.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第9章 曲线积分与曲面积分 第1节 对弧长的曲线积分.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第8章 重积分 第4节 三重积分的概念及计算.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第8章 重积分 第3节 二重积分的应用.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第8章 重积分 第2节 二重积分的计算.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第8章 重积分 第1节 二重积分的概念与性质.pdf
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(课件讲稿)第7章 多元函数微分及其应用 第7节 多元函数的极值及其求法.pdf
- 银川能源学院:《概率论与数理统计》课程教学资源(PPT课件讲稿)第二章 随机变量.ppt
- 银川能源学院:《概率论与数理统计》课程教学资源(PPT课件讲稿)第五章 大数定律与中心极限定理.ppt
- 银川能源学院:《概率论与数理统计》课程教学资源(PPT课件讲稿)第四章 随机变量的数字特征.ppt
- 银川能源学院:《复变函数与积分变换》课程教学资源(PPT课件讲稿)第一章 复数和复平面.ppt
- 银川能源学院:《复变函数与积分变换》课程教学资源(PPT课件讲稿)第七章 傅里叶变换.ppt
- 银川能源学院:《复变函数与积分变换》课程教学资源(PPT课件讲稿)第三章 复变函数的积分.ppt
- 银川能源学院:《复变函数与积分变换》课程教学资源(PPT课件讲稿)第九章 快速傅里叶变换.ppt
- 银川能源学院:《复变函数与积分变换》课程教学资源(PPT课件讲稿)第二章 解析函数.ppt
- 银川能源学院:《复变函数与积分变换》课程教学资源(PPT课件讲稿)第五章 留数理论及其应用.ppt
- 银川能源学院:《复变函数与积分变换》课程教学资源(PPT课件讲稿)第八章 拉普拉斯变换.ppt
- 银川能源学院:《复变函数与积分变换》课程教学资源(PPT课件讲稿)第六章 共形映射.ppt
- 银川能源学院:《复变函数与积分变换》课程教学资源(PPT课件讲稿)第四章 解析函数的级数表示法.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第1章 函数、极限与连续 0引言.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第1章 函数、极限与连续 1初等函数.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第1章 函数、极限与连续 2数列的极限.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第1章 函数、极限与连续 3函数的极限.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第1章 函数、极限与连续 4无穷小与无穷大.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第1章 函数、极限与连续 5极限的运算法则.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第1章 函数、极限与连续 6极限存在准则及两个重要极限.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第1章 函数、极限与连续 7无穷小的比较.ppt
