重庆工商大学：《统计学》课程教学课件（PPT讲稿）第9章 抽样与抽样估计

第九章 抽样与抽样估计 本章重点 1、影响抽样平均误差的因素 2、简单随机抽样下总体平均数和总 体成数的区间估计 重度工商大学 制作：数学与镜什学院，黄孟套

制作：数学与统计学院. 黄应绘 第九章 抽样与抽样估计 本章重点 2、简单随机抽样下总体平均数和总 体成数的区间估计 1、影响抽样平均误差的因素

§1抽样调查中常用的基本概念 一、抽样推断的概念 抽样推断是按随机原则从总体中抽 取部分单位进行观察，并根据样本的实 际数据对总体的数量特征作出具有一定 可靠程度的估计和判断。 制作：数学与就什学院，黄在套

制作：数学与统计学院. 黄应绘 一、抽样推断的概念 抽样推断是按随机原则从总体中抽 取部分单位进行观察，并根据样本的实 际数据对总体的数量特征作出具有一定 可靠程度的估计和判断。 §1 抽样调查中常用的基本概念

二、总体和样本 1、总体也称全及总体。指所要认识的研究 对象全体。总体单位总数用“N”表示。 2、样本也称抽样总体，是抽出的单位组成 的整体。样本单位总数用“n”表示。 重度工商大学 制作：数学与镜什学院，黄孟套

制作：数学与统计学院. 黄应绘 二、总体和样本 1、总体也称全及总体。指所要认识的研究 对象全体。总体单位总数用“N”表示。 2、样本也称抽样总体，是抽出的单位组成 的整体。样本单位总数用“ n”表示

三、总体指标和样本指标（参数与统计量） 1、针对总体计算的指标为总体指标， 也叫总体参数。 参数的值是定值 2、针对样本计算的指标为样本指标， 也叫统计量。 统计量的值随样本不同而不同，是随机变量。 抽样估计就是通过统计量的值估计参数的值。 制作：数学与就竹学院，黄在套

制作：数学与统计学院. 黄应绘 三、总体指标和样本指标（参数与统计量） 1、针对总体计算的指标为总体指标， 也叫总体参数。 参数的值是定值 2、针对样本计算的指标为样本指标， 也叫统计量。 统计量的值随样本不同而不同，是随机变量。 抽样估计就是通过统计量的值估计参数的值

四、样本容量和样本个数 1、样本容量 一个样本包含的单位数。用“n表示。 2、样本个数 从一个总体中可能抽取的样本数目， 用M表示 重度工商大学 制作：数学与镜计骨院，黄孟徐

制作：数学与统计学院. 黄应绘 四、样本容量和样本个数 1、样本容量 一个样本包含的单位数。用 “ n”表示。 2、样本个数 从一个总体中可能抽取的样本数目， 用M表示

五、抽样方法 (一)根据取样方式的不同， 抽样方法有重复抽样和不重复抽样两种。 1、重复抽样：也叫放回抽样。 一个单位可能中选多次 每次抽单位，概率相等。 抽样误差较大。 重废工商大学 制作：数学与就什学院，黄在套

制作：数学与统计学院. 黄应绘 1、重复抽样：也叫放回抽样。 一个单位可能中选多次 每次抽单位，概率相等。 五、抽样方法 （一）根据取样方式的不同， 抽样方法有重复抽样和不重复抽样两种。 抽样误差较大

2、不重复抽样：也叫无放回抽样。 一个单位最多中选一次 每次抽单位，概率不等，逐渐增加 抽样误差较小。 (二)根据对样本的要求不同，抽样方法又 有考虑顺序的抽样和不考虑顺序的抽样 重度工商大学 制作：数学与镜什学院，黄孟套

制作：数学与统计学院. 黄应绘 一个单位最多中选一次 每次抽单位，概率不等，逐渐增加 抽样误差较小。 2、不重复抽样：也叫无放回抽样。 （二）根据对样本的要求不同，抽样方法又 有考虑顺序的抽样和不考虑顺序的抽样

(三)两种分类的交叉 考虑顺序的不重复抽样数目A 考虑顺序的重复抽样数目B%=N” 不考虑顺序的不重复抽样数目C% 不考虑顺序的重复抽样数目〈 六、抽样误差 1、抽样误差常指随机性误差。 制作：数学与就什学院，黄在套

制作：数学与统计学院. 黄应绘 （三）两种分类的交叉 考虑顺序的不重复抽样数目 考虑顺序的重复抽样数目 不考虑顺序的不重复抽样数目 不考虑顺序的重复抽样数目 n AN n n B N N = n CN 1 n CN n + + 六、抽样误差 1、抽样误差常指随机性误差

2、有实际抽样误差、抽样平均误差、 抽样极限误差。 3、实际抽样误差：指某一具体样本估计值 与总体参数的真实值之间的离差。 4、抽样平均误差，指样本统计量的标准差。 例：从1、2、3中抽2个（重复)，参数取 总体平均数X(等于2)，则实际抽样误差 如下： 重度工商大学 制作：数学与镜什学院.黄后套

制作：数学与统计学院. 黄应绘 2、有实际抽样误差、抽样平均误差、 抽样极限误差。 3、实际抽样误差：指某一具体样本估计值 与总体参数的真实值之间的离差。 4、抽样平均误差，指样本统计量的标准差。 例：从1、2、3中抽2个（重复），参数取 总体平均数 （等于2），则实际抽样误差 如下： X

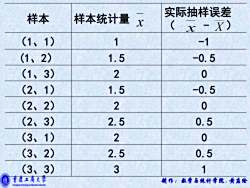
样本 样本统计量 实际抽样误差 （x-X） (1、1) 1 -1 (1、2) 1.5 -0.5 (1、3) 2 0 (2、1) 1.5 -0.5 (2、2) 2 0 (2、3) 2.5 0.5 (3、1) 2 0 (3、2) 2.5 0.5 (3、3) 3 1 @重度工商大茅 制作：数学与铣竹学院，黄孟徐

制作：数学与统计学院. 黄应绘 样本 样本统计量 实际抽样误差 （ - ） （1、1） 1 -1 (1、2） 1.5 -0.5 （1、3） 2 0 （2、1） 1.5 -0.5 （2、2） 2 0 （2、3） 2.5 0.5 （3、1） 2 0 （3、2） 2.5 0.5 （3、3） 3 1 x x X