重庆工商大学：《统计学》课程授课教案（讲义）第五章 分布的数值特征

第五章分布的数值特征 本章重点 1、算术平均数的计算 2、调和平均数的计算 3、标准差和标准差系数的应用 §1平均指标 统计中的平均数是用以表明数据的集中趋势的指标。它是统计分析中最常用 的一种统计指标。世界各国，特别是欧、美的统计学家都特别重视平均数的意义 和作用。其实，统计分析中的其它分析方法，如离差、相关、回归、指数等，在 某种意义上也含有平均的性质。因此，英国统计学家鲍莱认为统计学可称为“平 均数的科学”。本节要给大家介绍算术平均数、调和平均数、几何平均数、中位 数、众数。 一、算术平均数 (一)计算公式 1、当数据没分组时，直接将各数据相加，用和除以数据个数即可。 称为简单算术平均数。 n 2、当数据分了组时，用加权算术平均数。 Ex.f. Y= 对单项式数列，直接代入即可：对组距式数列，要先求出各组组中值作为各 组的代表值，再进行计算。 例51：某企业100个职工的工资如下表，试计算该企业职工的平均工资 表5-1职工工资统计表 工资（元）x职工人数（人）f组中值x:xf 900以下 10 8958950 900-910 10 90519050 910-920 40 91536600 920-930 30 92527750 930以上 9359350

第五章 分布的数值特征 本 章 重 点 1、算术平均数的计算 2、调和平均数的计算 3、标准差和标准差系数的应用 §1 平 均 指 标 统计中的平均数是用以表明数据的集中趋势的指标。它是统计分析中最常用 的一种统计指标。世界各国，特别是欧、美的统计学家都特别重视平均数的意义 和作用。其实，统计分析中的其它分析方法，如离差、相关、回归、指数等，在 某种意义上也含有平均的性质。因此，英国统计学家鲍莱认为统计学可称为“平 均数的科学”。本节要给大家介绍算术平均数、调和平均数、几何平均数、中位 数、众数。 一、算术平均数 （一）计算公式 1、当数据没分组时，直接将各数据相加，用和除以数据个数即可。 称为简单算术平均数。 n X n i xi = = 1 2、当数据分了组时，用加权算术平均数。 X =   = = n i i n i i i f x f 1 1 . . 对单项式数列，直接代入即可；对组距式数列，要先求出各组组中值作为各 组的代表值，再进行计算。 例 51： 某企业 100 个职工的工资如下表，试计算该企业职工的平均工资。 表 5-1 职工工资统计表 工资（元）x 职工人数（人）f 组中值 x xf 900 以下 10 895 8950 900-910 10 905 9050 910-920 40 915 36600 920-930 30 925 27750 930 以上 10 935 9350

解： 立xf:-9170917(元) = 100 (二)影响加权算术平均数的因素 1、看以下三例： 2 表5-2甲乙两班成绩统计表 ①例5-2： 性别平均成绩（分）X人数 甲班乙班（人） 男8075 20 女858020 得各班平均成绩： X-82分 x2=77分 结果：相酮（比重相酮，X不码，则平均数（）不同。 ②例5-3： 表5-3甲乙两市场销售统计表 产品价格（元/斤） 成交量（万斤）f X 甲市场乙市场 用 12 1 1.4 丙 15 得各市场平均价格： X甲=1.375元 X2=1.325元 结果：f不同（实质是比重 不同)，X相同，则平均数（灭）不同。 ③例5-4： 表5-4甲乙两组年龄统计表 性别平均年龄（岁）人数「 甲组乙组 30 615 女 20 1435 得各组的平均年龄：X甲=23岁 x2=23岁

解： X =   = = n i i n i i i f x f 1 1 . . = 100 91700 =917（元） （二）影响加权算术平均数的因素 1、看以下三例： 2、 表 5-2 甲乙两班成绩统计表 ① 例 5-2： 得各班平均成绩： x甲 =82 分 x乙 =77 分 结果：f 相同（比重  f f 相同），X 不同，则平均数（ X ）不同。 ② 例 5-3： 表 5-3 甲乙两市场销售统计表 产品 价格（元/斤） X 成交量（万斤）f 甲市场 乙市场 甲 1.2 1 2 乙 1.4 2 1 丙 1.5 1 1 得各市场平均价格： x甲 =1.375 元 x乙 =1.325 元 结果：f 不同（实质是比重  f f 不同），X 相同，则平均数（ X ）不同。 ③ 例 5-4： 表 5-4 甲乙两组年龄统计表 得各组的平均年龄： x甲 =23 岁 x乙 =23 岁 性别 平均成绩（分）X 人数 甲班 乙班 （人）f 男 80 75 30 女 85 80 20 性别 平均年龄（岁） X 人数 f 甲组 乙组 男 30 6 15 女 20 14 35

结果：不同（但是比重克相同，X相同，则平约数（了）相同。 2、从以上三例可得结论：影响加权算术平均数的因素有二，即各组变量值(X) 的大小和各组权数所古比藏（)的大小。 3、通过公式变形也可得到以上结论： + ∑f =2x (三)权数的选择 对绝对数求平均数时，频数一般都是权数。但对相对数求平均数时，频数不 一定是权数。见下例： 例5-5某企业25个班组按工人劳动生产率分组资料如下： 表55某企业劳动生产率统计表 工人劳动生产率（件人）生产班组数工人数 50-60 10 150 60-70 100 70-80 70 80-90 30 90以上. 16 求：这25个班组的平均劳动生产率 解：平均劳动生产率=总产量_∑ 总人数∑了 =55*150+65*100+75*70+85*30+95*16 366 =65.77(件/人) 此时，工人数为权数，而生产班组数是频数

结果：f 不同（但是比重  f f 相同），X 相同，则平均数（ X ）相同。 2、从以上三例可得结论：影响加权算术平均数的因素有二，即各组变量值（X） 的大小和各组权数所占比重（  f f ）的大小。 3、通过公式变形也可得到以上结论： X =   f xf =  f x f 1 1 +  f x f 2 2 + . +  f n x f n =x1.  f f 1 +x2.  f f 2 + . +xn.  f f n =( . )  f f x （三）权数的选择 对绝对数求平均数时，频数一般都是权数。但对相对数求平均数时，频数不 一定是权数。见下例： 例 5-5 某企业 25 个班组按工人劳动生产率分组资料如下： 表 5-5 某企业劳动生产率统计表 工人劳动生产率（件/人） 生产班组数 工人数 50-60 10 150 60-70 7 100 70-80 5 70 80-90 2 30 90 以上 1 16 求：这 25 个班组的平均劳动生产率 解：平均劳动生产率= 总人数 总产量 =   f xf = 366 55*150 + 65*100 + 75*70 + 85*30 + 95*16 =65.77（件/人） 此时，工人数为权数 f，而生产班组数是频数

结论：对相对数求平均数时，以该相对数原始公式中的分母资料作权数F。 (四)算术平均数的数学性质 1、各变量值与其均值的离差之和等于零，即∑x,-)=0 2、各变量值与其均值的离差平方和最小，即上(x,一)-最小(min) 3、如果变量X与变量Y之间的关系是Y=abX,其中为常数，则 Y=atbX 二、调和平均数 1、调和平均数是算术平均数的一种变形。 2、己知x的文字公式中的母项()资料时，用加权算术平均数 己知x的文字公式中的子项(m)资料时，用加权调和平均数 三、几何平均数(GM) (一)概令 它是N个单位的变量值的连乘积的N次方根。凡是变量值的连乘积等于总比 率或总速度时，都可使用几何平均数。 (二)计算公式 1、资料未分组时，用简单几何平均数：GM=x 例5-6某厂生产某种零件经过四个车间，各车间合格率依次为95%、92%、90%、 94%,则平均合格率=/95%*92%*90%*94%=92.73% 2、资料分组时，用加权几何平均数：GM=∑x (三)几何平均数也可以看作均值的一种变形，对简单几何平均数两端取对数得： (四)几何平均数是一种具有特殊用途的平均数。在世界各国的政府统计工作中， 主要在两种场合运用几何平均数。一是用于某种比率的平均数，如用于指数分析： 二是用于计算大致具有几何级数关系的一组数字的平均数。如世界各国都用它计 算经济指标的平均发展速度。 四、众数(M 1、它是总体中出现次数最多的变量值。众数在实际中用得较多。比如，制鞋厂 要制造适合大多数人穿的鞋：商店要计算不同时期的购物人次的众数或购物数量 的众数，以合理设置商业网点：修建人行天桥要确定过街人数的众数， 2、对未分组资料和单项式数列，直接找出即可。对组距式数列，先找出众数组

结论：对相对数求平均数时，以该相对数原始公式中的分母资料作权数 F。 （四）算术平均数的数学性质 1、各变量值与其均值的离差之和等于零，即 = − n i i x x 1 ( ) =0 2、各变量值与其均值的离差平方和最小，即  − = n i xi x 1 2 ( ) =最小（min） 3、如果变量 X 与变量 Y 之间的关系是 Yi=a+bXi,其中为常数，则 Y =a+b X 二、调和平均数 1、调和平均数是算术平均数的一种变形。 2、已知 x 的文字公式中的母项（f）资料时，用加权算术平均数 已知 x 的文字公式中的子项（m）资料时，用加权调和平均数 三、几何平均数（GM） （一）概念 它是 N 个单位的变量值的连乘积的 N 次方根。凡是变量值的连乘积等于总比 率或总速度时，都可使用几何平均数。 （二）计算公式 1、资料未分组时，用简单几何平均数 ： GM= n x 例 5-6 某厂生产某种零件经过四个车间，各车间合格率依次为 95%、92%、90%、 94%，则 平均合格率= 4 95%*92%*90%*94% =92.73% 2、资料分组时，用加权几何平均数 ：GM=   f f x （三）几何平均数也可以看作均值的一种变形，对简单几何平均数两端取对数得： （四）几何平均数是一种具有特殊用途的平均数。在世界各国的政府统计工作中， 主要在两种场合运用几何平均数。一是用于某种比率的平均数，如用于指数分析； 二是用于计算大致具有几何级数关系的一组数字的平均数。如世界各国都用它计 算经济指标的平均发展速度。 四、众数（M0） 1、它是总体中出现次数最多的变量值。众数在实际中用得较多。比如，制鞋厂 要制造适合大多数人穿的鞋；商店要计算不同时期的购物人次的众数或购物数量 的众数，以合理设置商业网点；修建人行天桥要确定过街人数的众数。 2、对未分组资料和单项式数列，直接找出即可。对组距式数列，先找出众数组

(次数最多的组)，再按公式计算 M0=L+ f-f i,其中，L表众数组的下限、i表众数组的组距、 (f-f)+(-f) ￡1表众数组之前那一组的次数、1表众数组之后那一组的次数 例5-7：某市某年职工家庭收支的抽样资料如下，求人均月收入的众数。 表3-6某市职工家庭收支表 人均月收入（元）户数 100-200 50 20-300 250 300-400 320 400-500 950 500-600 200 00以上 180 解：众数组为第四组 ff. Mo=L+ 950-320 i=400 (-f)+(-f) (950-320)+(950-200*100=456 3、利用以上公式计算众数时，假定数据分布具有明显的集中趋势，机假定众数 所在组与相邻两组的频数之差反映了数据分布陡峭上升而缓慢下降这一特征，同 时假定众数组的频数在该组内是均匀分布的。 4、众数的特点：是一种位置平均数：无明显集中趋势时，计算众数没有意义。 5、根据各国惯例，众数用得最多的是具有明显偏态分布的数列。 五、中位数(M) 1、处于中间位置的数为中位数。 2、中位数的确定：①资料未分组时，直接找出即可。当奇数个单位时，中位数 所处的位置为(N+1)2:当偶数个单位时，中位数为第N/2个与第(N+1)2 个数的简单算数平均数。 ②资料分组时，先确定中位数所在的组（第∑∫2所在的组），再通过以下公式计 ∑f 算中位数的近似值 Me =L+-2 5二，式中，L为中位数所在组的下 f 限，Sm1为中位数所在组以前各组的累积频数，m为中位数所在组的频数，i为 中位数所在组的组距

（次数最多的组），再按公式计算： M0=L+ i f f f f f f * ( ) ( ) 1 1 1 − + − − + − − , 其中，L 表众数组的下限、i 表众数组的组距、 f-1 表众数组之前那一组的次数、 f+1 表众数组之后那一组的次数。 例 5-7： 某市某年职工家庭收支的抽样资料如下，求人均月收入的众数。 表 3-6 某市职工家庭收支表 人均月收入（元） 户数 100-200 50 200-300 250 300-400 320 400-500 950 500-600 200 600 以上 180 解： 众数组为第四组 M0=L+ i f f f f f f * ( ) ( ) 1 1 1 − + − − + − − =400+ *100 (950 320) (950 200) 950 320 − + − − =445.6 3、利用以上公式计算众数时，假定数据分布具有明显的集中趋势，机假定众数 所在组与相邻两组的频数之差反映了数据分布陡峭上升而缓慢下降这一特征，同 时假定众数组的频数在该组内是均匀分布的。 4、众数的特点：是一种位置平均数；无明显集中趋势时，计算众数没有意义。 5、根据各国惯例，众数用得最多的是具有明显偏态分布的数列。 五、中位数（Me） 1、处于中间位置的数为中位数。 2、中位数的确定：① 资料未分组时，直接找出即可。当奇数个单位时，中位数 所处的位置为（N+1）/2；当偶数个单位时，中位数为第 N/2 个与第（N+1）/2 个数的简单算数平均数。 ②资料分组时,先确定中位数所在的组（第  f /2 所在的组），再通过以下公式计 算中位数的近似值。 Me = i f L f s m m * 2 −1 − +  ，式中，L 为中位数所在组的下 限，Sm-1 为中位数所在组以前各组的累积频数，fm 为中位数所在组的频数，i 为 中位数所在组的组距

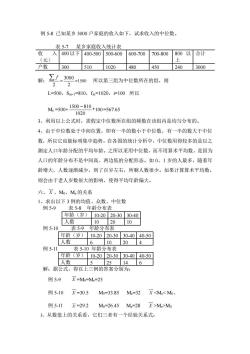
例5-8已知某乡3000户家庭的收入如下，试求收入的中位数， 表5-7某乡家庭收入统计表 收入400以下400-500500-600600-700700-800800以合计 (元) 上 户数3005101020480450240☐3000 解：3000=1500所以第三组为中位数所在的组，则 L=500,Sm-1=810,fm=1020,户100所以 M=500+1500-81010=567.65 1020 3、利用以上公式时，需假定中位数所在组的频数在该组内是均匀分布的。 4、由于中位数处于中间位置，即有一半的数小于中位数，有一半的数大于中位 数，所以它也能标明集中趋势。在各国的统计分析中，中位数用得较多的是以之 测定人口年龄分配的平均年龄。之所以采用中位数，而不用算术平均数，是因为 人口的年龄分布不是中间高、两边低的分配形态。如0、1岁的人最多，随着年 龄增大，人数逐渐减少，到了百岁左右，所剩人数很少。如果计算算术平均数， 则会由于老人岁数很大的影响，使得平均年龄偏大。 六、X、Mo、M的关系 1、求出以下3例的均值、众数、中位数 例5-9 表5-8年龄分布表 年龄（岁）10-2020-3030-40 人数 10 2010 例5-10 表5-9年龄分布表 年龄（岁）10-2020-3030-4040-50 人 6 10204 例5-11 表5-10年龄分布表 年龄（岁）10-2020-3030-4040-50 人数 525 146 解：据公式，得以上三例的答案分别为： 例5-9X=M0=Me=25 例5-10X=30.5 M0=33.85 Me=32 XM>M0 3、从数值上的关系看，它们三者有一个经验关系式：

例 5-8 已知某乡 3000 户家庭的收入如下，试求收入的中位数。 表 5-7 某乡家庭收入统计表 收 入 （元） 400以下 400-500 500-600 600-700 700-800 800 以 上 合计 户数 300 510 1020 480 450 240 3000 解： 2  f = 2 3000 =1500 所以第三组为中位数所在的组，则 L=500，Sm-1=810，fm=1020，i=100 所以 Me =500+ *100 1020 1500 − 810 =567.65 3、利用以上公式时，需假定中位数所在组的频数在该组内是均匀分布的。 4、由于中位数处于中间位置，即有一半的数小于中位数，有一半的数大于中位 数，所以它也能标明集中趋势。在各国的统计分析中，中位数用得较多的是以之 测定人口年龄分配的平均年龄。之所以采用中位数，而不用算术平均数，是因为 人口的年龄分布不是中间高、两边低的分配形态。如 0、1 岁的人最多，随着年 龄增大，人数逐渐减少，到了百岁左右，所剩人数很少。如果计算算术平均数， 则会由于老人岁数很大的影响，使得平均年龄偏大。 六、 X 、M0、Me 的关系 1、求出以下 3 例的均值、众数、中位数 例 5-9 表 5-8 年龄分布表 年龄（岁） 10-20 20-30 30-40 人数 10 20 10 例 5-10 表 5-9 年龄分布表 年龄（岁） 10-20 20-30 30-40 40-50 人数 6 10 20 4 例 5-11 表 5-10 年龄分布表 年龄（岁） 10-20 20-30 30-40 40-50 人数 5 25 14 6 解：据公式，得以上三例的答案分别为： 例 5-9 X =M0=Me=25 例 5-10 X =30.5 M0=33.85 Me=32 X Me>M0 3、从数值上的关系看，它们三者有一个经验关系式：

X-M=(X-Mo) 4、当数据呈对称分布或接近对称分布时，应选均值作为集中趋势的代表值，但 它只适合定距和定比尺度的数据；当数据为偏态分布，特别是偏斜程度较大时， 应选众数或中位数作为集中趋势的代表值，它们适合所有尺度的数据。 $2分布离散程度的测度 集中趋势只是数据分布的一个特征，它所反映的是各变量值向其中心值聚集 的程度。而各变量值之间的差异状况如何呢？这就需要考察数据的分散程度。数 据的分散程度是数据分布的另一个重要特征，它所反映的是各变量值远离其中心 值的程度，因此，也称为离中趋势。其可以用于评价平均数的代表性大小。数据 的离散程度越大，集中趋势的测度值对该组数据的代表性就越差，离散程度越小 其代表性就越好。 描述数据离散程度的测度值主要有极差（全距）、平均差、方差和标准差、 离散系数等。 一、极差（全距）R 1、R=最大值.最小值或最大组上限.最小组下限 2、例5-12有甲、乙两组数据，试比较哪组均值平均数的代表性大。 甲：40608084：乙：63656670 解：因为 子出 ,有柳66 x2=66 R=84-40=44R2=70-63=77<44 所以，乙组均值的代表性大 二、平均差(MD) 1、简单平均差MD=-习 如上例中MD=40-6+60-66+80-6+84-66=16 4 MDz=63-6d+65-6d+66-6d+70-6d2 4 2<16,所以，乙组均值的代表性大

X - Me= 3 1 （ X - M0） 4、当数据呈对称分布或接近对称分布时，应选均值作为集中趋势的代表值，但 它只适合定距和定比尺度的数据；当数据为偏态分布，特别是偏斜程度较大时， 应选众数或中位数作为集中趋势的代表值，它们适合所有尺度的数据。 §2 分布离散程度的测度 集中趋势只是数据分布的一个特征，它所反映的是各变量值向其中心值聚集 的程度。而各变量值之间的差异状况如何呢？这就需要考察数据的分散程度。数 据的分散程度是数据分布的另一个重要特征，它所反映的是各变量值远离其中心 值的程度，因此，也称为离中趋势。其可以用于评价平均数的代表性大小。数据 的离散程度越大，集中趋势的测度值对该组数据的代表性就越差，离散程度越小， 其代表性就越好。 描述数据离散程度的测度值主要有极差（全距）、平均差、方差和标准差、 离散系数等。 一、极差（全距）R 1、R=最大值- 最小值或最大组上限- 最小组下限 2、例 5-12 有甲、乙两组数据，试比较哪组均值平均数的代表性大。 甲：40 60 80 84 ；乙：63 65 66 70 解：因为 n X n i xi = = 1 ，有 x甲 =66 x乙 =66 R 甲=84-40=44 R 乙=70-63=7 7<44 所以，乙组均值的代表性大 二、平均差（MD） 1、简单平均差 MD= n  x − x 如上例中 MD 甲= 4 40 − 66 + 60 − 66 + 80 − 66 + 84 − 66 =16 MD 乙= 4 63 − 66 + 65 − 66 + 66 − 66 + 70 − 66 =2 2<16 ，所以，乙组均值的代表性大

2,加权平均差MD=∑k- ∑f 三、方差和标准差 方差是各变量值与其均值离差平方的平均数。方差的平方根叫标准差，也叫均 方差。 (一)计算公式 1、总体标准差 ①资料未分组时，用简单标准差0- Σ- 用例5-12中的数据，得0= 26+6+14+18=175 3++0+425 0 4 即，仍然是乙组的均值的代表性强。 Zx-x ②、资料分组时，用加权标准差0Σ了 例513己知某厂200个工人按日产量分组如下：试求其标准差。 表5-8产量统计表 日产量（件）工人数 20-30 10 30-40 70 40-50 90 50-60 30 Ex.f. x= =42(件) 0= Σ-xf1T+7+3+13」 >f W10+70+90+30 220-781(件) 200 2、样本标准差

2、加权平均差 MD=   − f x x f 三、方差和标准差 方差是各变量值与其均值离差平方的平均数。方差的平方根叫标准差，也叫均 方差。 （一）计算公式 1、总体标准差 ①资料未分组时，用简单标准差 Ó= ( ) n  x−x 2 用例 5-12 中的数据，得 Ó 甲= 4 26 6 14 18 2 2 2 2 + + + =17.55 Ó 乙= 4 3 1 0 4 2 2 2 2 + + + =2.55 即，仍然是乙组的均值的代表性强。 ②、资料分组时，用加权标准差 Ó= ( )   − f x x * f 2 例 5-13 已知某厂 200 个工人按日产量分组如下：试求其标准差。 表 5-8 产量统计表 日产量（件） 工人数 20-30 10 30-40 70 40-50 90 50-60 30 解： X =   = = n i i n i i i f x f 1 1 . . =42（件） Ó= ( )   − f x x * f 2 = 10 70 90 30 17 7 3 13 2 2 2 2 + + + + + + = 200 12200 . =7.81(件) 2、样本标准差

E-】s如r S-1n-1 -x5 ∑f-1 其中，1称为自由度。 例如，我们仍用例5-13中的数据，计算的样本标准差为： S-1= E(x-x) ∑f-1 220-7.83(件) V200-11 (二)标准差的数学性质 标准差的平方为方差，所以标准差也叫均方差。 、o2=x-) E勇：ok-.2x-27+).工x-2+句 =x2付+=-) 2、如Y=a过bX,则0y=bOx 证明：Y=a时bX,则7=atb方 所以，0，= Eash ai) E-天】.0 3、0为最小值，即-sΣk-4 n ,其中A为任意常数 四、离散系数 1、利用R、O比较两数列离散程度或平均数代表性大小的条件 ①两数列的平均数相等。R、O的大小要受原变量值本身水平高低的影响， 也就是与变量的均值大小有关，变量值绝对水平越高，离散程度的测度值自然就 大，绝对水平越低，离散程度的测度值自然就小。所以对平均数不等的数列，就 不能用R、O比较。 ②两数列的计量单位相同。采用不同计量单位计量的变量值，其离散程度的 测度值也就不同，不能直接比较。此时，也不能用R、O比较。 如果不满足上述条件，则应该用离散系数来判断。有全距系数、平均差系数

Sn-1= ( ) 1 2 −  − n x x 或 Sn-1= ( ) 1 * 2  −  − f x x f 其中，n-1 称为自由度。 例如，我们仍用例 5-13 中的数据，计算的样本标准差为： Sn-1= ( ) 1 * 2  −  − f x x f = 200 1 12200 . − =7.83(件) （二）标准差的数学性质 标准差的平方为方差，所以标准差也叫均方差。 1、Ó2= x 2 -(x) 2 证明：Ó2= ( ) n  x−x 2 = ( ) n  x X X x       − + 2 2 2 = ( ) n x − xx + n x 2 2 2 = x 2 - 2 (x) 2 + (x) 2 = x 2 -(x) 2 2、如 Y= a+bX，则 Óy= bÓx 证明：Y= a+bX，则 Y =a+b X 所以，Óy= ( ) n  a+bx−a+bx 2 = b ( ) n  x−x 2 = bÓx 3、Ó2 为最小值，即 ( ) n  x−x 2 ≤ ( ) n  x−A 2 ，其中 A 为任意常数 四、离散系数 1、利用 R、Ó 比较两数列离散程度或平均数代表性大小的条件 ① 两数列的平均数相等。R、Ó 的大小要受原变量值本身水平高低的影响， 也就是与变量的均值大小有关，变量值绝对水平越高，离散程度的测度值自然就 大，绝对水平越低，离散程度的测度值自然就小。所以对平均数不等的数列，就 不能用 R、Ó 比较。 ② 两数列的计量单位相同。采用不同计量单位计量的变量值，其离散程度的 测度值也就不同，不能直接比较。此时，也不能用 R、Ó 比较。 如果不满足上述条件，则应该用离散系数来判断。有全距系数、平均差系数

标准差系数。但一般指标准差系数。 2、具体计算 Vwg或Vs=月 例5-14某县工行和农行三个储蓄所1月份的储蓄额如下，试判断哪一个银 行的储蓄所之间的储蓄更均衡。 工行：13、18、14农行：50、51、91 (单位：万元) 解：由了=女 n ，得x=15万元 术64万元 Σ-】 又由0-一n ,得0=2.16万元0=19.1万元 则V0r=2.16/15=14.4% V0=19.1/64=29.84% 所以，工行各储蓄所之间的储蓄更均衡

标准差系数。但一般指标准差系数。 2、具体计算 VÓ= x  或 VS= x s 例 5-14 某县工行和农行三个储蓄所 1 月份的储蓄额如下，试判断哪一个银 行的储蓄所之间的储蓄更均衡。 工行：13、18、14 农行：50、51、91 （单位：万元） 解：由 n X n i xi = = 1 ，得 x工 =15 万元 x农 =64 万元 又由 Ó= ( ) n  x−x 2 ，得 Ó 工=2.16 万元 Ó 农=19.1 万元 则 VÓ 工=2.16/15=14.4% VÓ 农=19.1/64=29.84% 所以，工行各储蓄所之间的储蓄更均衡