《统计学》课程授课教案（讲义）第五章 统计指数

第五章统计指数（一）教学目的通过本章的学习，使学生正确理解指数的概念和作用，从而掌握各种指数的编制原理和计算方法。（二）基本要求要求掌握指数的概念、性质、种类和作用，学会编制综合指数、平均数指数及平均指标指数，并能将不同的指数区分开来，进一步学会利用指数体系进行因素分析。（三）教学要点1、指数的概念与种类；2、总指数的编制方法：3、平均指标指数的编制方法；4、指数体现与因素分析：5、指数数列的编制及类型。（四）本章难点1、广义指数与狭义指数的区分；2、数量指数与质量指数的区分；3、指数化因素与同度量因素的区分；4、综合指数与平均数指数的联系：5、平均数指与平均指标指数的区分。（五）教学时数6—8课时（六）教学内容本章共分四节：第一节统计指数概述一、统计指数的概念广义上说，指数是指用来反映研究所研究社会经济现象总体数量变动状况的相对

第五章 统计指数 （一）教学目的 通过本章的学习，使学生正确理解指数的概念和作用，从而掌握各种指数的编制原 理和计算方法。 （二）基本要求 要求掌握指数的概念、性质、种类和作用，学会编制综合指数、平均数指数及平均 指标指数，并能将不同的指数区分开来，进一步学会利用指数体系进行因素分析。 （三）教学要点 1、指数的概念与种类； 2、总指数的编制方法； 3、平均指标指数的编制方法； 4、指数体现与因素分析； 5、指数数列的编制及类型。 （四）本章难点 1、广义指数与狭义指数的区分； 2、数量指数与质量指数的区分； 3、指数化因素与同度量因素的区分； 4、综合指数与平均数指数的联系； 5、平均数指与平均指标指数的区分。 （五）教学时数 6—8 课时 （六）教学内容 本章共分四节： 第一节 统计指数概述 一、统计指数的概念 广义上说，指数是指用来反映研究所研究社会经济现象总体数量变动状况的相对

数。狭义上说，指数是指用来综合反映所研究社会经济现象复杂总体数量变动状况的相对数。二、 统计指数的分类按所反映的对象范围不同，统计指数分为个体指数和总指数。按所表明现象的数量特征不同，统计指数分为数量指标指数和质量指标指数。总指数按其所采用的指标形式不同，可以分为综合指数与平均指数。按比较对象不同，统计指数可分时间性指数、地区性指数和计划完成指数。在指数数列中按所采用的基期不同，统计指数可分为定基指数和环比指数三、统计指数的性质1.综合性。2.代表性。3.相对性。4.平均性。四、指数在经济分析中的作用1.综合地反映复杂经济现象总体的变动方向和程度。2.分析在现象总体的变动中，各构成因素影响的大小。第二节乡综合指数一、综合指数的概念及计算的一般原理指数方法论主要是研究总指数的计算问题，总指数的编制方法，其基本形式有两种：一是综合指数，二是平均指数。两种方法有一定的联系，但各有其特点。综合指数是对两个时期范围相同的复杂现象总体总量指标对比形成的指数，在总量指标中包含两个或两个以上的因素，将其中被研究因素以外的一个或一个以上的因素适定下来，仅观察被研究因素的变动，这样编制的指数，称为综合指数。综合指数的重要意义，是它能够比较全面、准确地反映所研究的现象总体总的变动程度和随之产生的绝对数效果。它的特点是先综合后对比。其编制方法是：首先引入同度量因素，解决复杂总体在研究指标上不能直接综合的困难，使其可以计算出总体的综合总量；其次，将同度量因素固定，以消除同度量因素变动的影响；最后将两个时期的总量对比，其结果即为综合1

1 数。 狭义上说，指数是指用来综合反映所研究社会经济现象复杂总体数量变动状况的相 对数。 二、统计指数的分类 按所反映的对象范围不同，统计指数分为个体指数和总指数。 按所表明现象的数量特征不同，统计指数分为数量指标指数和质量指标指数。 总指数按其所采用的指标形式不同，可以分为综合指数与平均指数。 按比较对象不同，统计指数可分时间性指数、地区性指数和计划完成指数。 在指数数列中按所采用的基期不同，统计指数可分为定基指数和环比指数。 三、统计指数的性质 1.综合性。 2.代表性。 3.相对性。 4.平均性。 四、指数在经济分析中的作用 1.综合地反映复杂经济现象总体的变动方向和程度。 2.分析在现象总体的变动中，各构成因素影响的大小。 第二节 综合指数 一、综合指数的概念及计算的一般原理 指数方法论主要是研究总指数的计算问题，总指数的编制方法，其基本形式有两种： 一是综合指数，二是平均指数。两种方法有一定的联系，但各有其特点。 综合指数是对两个时期范围相同的复杂现象总体总量指标对比形成的指数，在总量 指标中包含两个或两个以上的因素，将其中被研究因素以外的一个或一个以上的因素固 定下来，仅观察被研究因素的变动，这样编制的指数，称为综合指数。 综合指数的重要意义，是它能够比较全面、准确地反映所研究的现象总体总的变动 程度和随之产生的绝对数效果。 它的特点是先综合后对比。其编制方法是：首先引入同度量因素，解决复杂总体在 研究指标上不能直接综合的困难，使其可以计算出总体的综合总量；其次，将同度量因 素固定，以消除同度量因素变动的影响；最后将两个时期的总量对比，其结果即为综合

指数，也就综合地反映了复杂总体研究指标的变动。例如甲乙两种产品，由于使用价值不同，计量单位不同，其产量是不能直接相加的，但不同产品的价值量可以相加。因此，我们可以利用产值与产量和价格之间的联系，将产量乘以各自的价格，得到产值，则两种产品便可以加总了。这里，价格起到将不同产品同度量的作用，被称为同度量因素。我们所要研究的指标一一产量，被称为指数化指标。如果我们的任务是研究甲乙两种产品的价格变动情况，同样的道理，则可把价格作为指数化指标，仍然依据产值、价格与产量间的经济联系，把产量作为同度量因素，从而将两种产品综合起来。同时还要将同度量因素固定，消除同度量因素变动的影响。在本例中，作为同度量因素的价格，报告期对基期也可能发生变动，这样，将两个时期的产值对比，就不仅受到产品产量变动的影响，同时也受到两个时期价格变动的影响。因此，需要将价格固定，即两个时期的产值，均采用同一时期的价格计算，借以消除价格变动的影响。将采用同一时期价格计算的两个产值对比，其结果仅受到两种产品不同时期产量变动的影响，从而达到综合反映两种产品产量变动的目的。实际应用中，还有一个重要的问题需要解决，即固定的同度量因素所属时期的选择问题。究竞固定在报告期还是固定在基期，十分重要，因为同度量因素不仅起同度量的作用，而且具有加权的作用，用不同时期的同度量因素计算，会得到不同的综合指数结果。二、数量指标综合指数的编制现以商品销售量综合指数的编制为例来说明数量指标综合指数编制的一般原则和方法。现以I代表销售量总指数，于是有：（1）用基期价格为同度量因素（加权），公式为：ZqiPoIg=ZqoPo上述公式又称拉氏数量指数公式，它是1864年由德国学者拉斯贝尔提出的。（2）用报告期价格为同度量因素（加权），公式为：ZqpiI.=Zqop这个公式又称派氏数量指数公式，它是1874年德国学者派许提出的。从理论上讲上述两个公式均可成立，但在实际工作中，编制销售量综合指数时，一般均采用基期价格作为同度量因素。这是因为编制销售量综合指数的目的，是在于要排2

2 指数，也就综合地反映了复杂总体研究指标的变动。 例如甲乙两种产品，由于使用价值不同，计量单位不同，其产量是不能直接相加的， 但不同产品的价值量可以相加。因此，我们可以利用产值与产量和价格之间的联系，将 产量乘以各自的价格，得到产值，则两种产品便可以加总了。这里，价格起到将不同产 品同度量的作用，被称为同度量因素。我们所要研究的指标——产量，被称为指数化指 标。如果我们的任务是研究甲乙两种产品的价格变动情况，同样的道理，则可把价格作 为指数化指标，仍然依据产值、价格与产量间的经济联系，把产量作为同度量因素，从 而将两种产品综合起来。同时还要将同度量因素固定，消除同度量因素变动的影响。在 本例中，作为同度量因素的价格，报告期对基期也可能发生变动，这样，将两个时期的 产值对比，就不仅受到产品产量变动的影响，同时也受到两个时期价格变动的影响。因 此，需要将价格固定，即两个时期的产值，均采用同一时期的价格计算，借以消除价格 变动的影响。将采用同一时期价格计算的两个产值对比，其结果仅受到两种产品不同时 期产量变动的影响，从而达到综合反映两种产品产量变动的目的。实际应用中，还有一 个重要的问题需要解决，即固定的同度量因素所属时期的选择问题。究竟固定在报告期 还是固定在基期，十分重要，因为同度量因素不仅起同度量的作用，而且具有加权的作 用，用不同时期的同度量因素计算，会得到不同的综合指数结果。 二、数量指标综合指数的编制 现以商品销售量综合指数的编制为例来说明数量指标综合指数编制的一般原则和 方法。 现以Iq代表销售量总指数，于是有： （1）用基期价格为同度量因素（加权），公式为：   = 0 0 1 0 q p q p I q 上述公式又称拉氏数量指数公式，它是1864年由德国学者拉斯贝尔提出的。 （2）用报告期价格为同度量因素（加权），公式为：   = 0 1 1 1 q p q p I q 这个公式又称派氏数量指数公式，它是1874年德国学者派许提出的。 从理论上讲上述两个公式均可成立，但在实际工作中，编制销售量综合指数时，一 般均采用基期价格作为同度量因素。这是因为编制销售量综合指数的目的，是在于要排

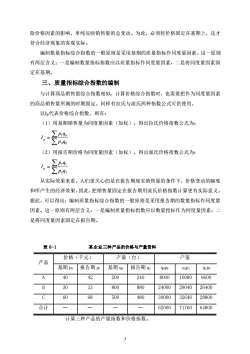
除价格因素的影响，单纯反映销售量的总变动。为此，必须将价格固定在基期上，这才符合经济现象的客观实际。编制数量指标综合指数的一般原则是采用基期的质量指标作同度量因素。这一原则有两层含义：一是编制数量指标指数应以质量指标作同度量因素，二是将同度量因素固定在基期。三、质量指标综合指数的编制与计算商品销售量综合指数相似，计算价格综合指数时，也需要把作为同度量因素的商品销售量所属的时期固定。同样有拉氏与派氏两种指数公式可供使用。以Ip代表价格综合指数，则有：（1）用基期销售量为同度量因素（加权），得出拉氏价格指数公式为：ZpidoI,=Zpoqo（2）用报告期价格为同度量因素（加权），得出派氏价格指数公式为：EpigIp=Epogi从实际效果来看，人们更关心的是在报告期现实销售量的条件下，价格变动的幅度和所产生的经济效果，因此，把销售量固定在报告期用派氏价格指数计算更有实际意义。据此，可以得出：编制质量指标综合指数的一般原则是采用报告期的数量指标作同度量因素。这一原则有两层含义：一是编制质量指标指数应以数量指标作为同度量因素；二是将同度量因素固定在报告期。表 6-1某企业三种产品的价格与产量资料产量（台）产值价格（千元）产品基期po报告期p基期qo报告期q1qopoqipiqipoA40422002409600800010080B3033264008008802400029040c6068500480300003264028800合计648006200071760-计算三种产品的产量指数和价格指数。3

3 除价格因素的影响，单纯反映销售量的总变动。为此，必须将价格固定在基期上，这才 符合经济现象的客观实际。 编制数量指标综合指数的一般原则是采用基期的质量指标作同度量因素。这一原则 有两层含义：一是编制数量指标指数应以质量指标作同度量因素，二是将同度量因素固 定在基期。 三、质量指标综合指数的编制 与计算商品销售量综合指数相似，计算价格综合指数时，也需要把作为同度量因素 的商品销售量所属的时期固定。同样有拉氏与派氏两种指数公式可供使用。 以Ip代表价格综合指数，则有： （1）用基期销售量为同度量因素（加权），得出拉氏价格指数公式为：   = 0 0 1 0 p q p q I p （2）用报告期价格为同度量因素（加权），得出派氏价格指数公式为：   = 0 1 1 1 p q p q I p 从实际效果来看，人们更关心的是在报告期现实销售量的条件下，价格变动的幅度 和所产生的经济效果，因此，把销售量固定在报告期用派氏价格指数计算更有实际意义。 据此，可以得出：编制质量指标综合指数的一般原则是采用报告期的数量指标作同度量 因素。这一原则有两层含义：一是编制质量指标指数应以数量指标作为同度量因素；二 是将同度量因素固定在报告期。 表 6-1 某企业三种产品的价格与产量资料 产品 价格（千元） 产量（台） 产值 基期 p0 报告期 p1 基期 q0 报告期 q1 q0p0 q1p1 q1p0 A 40 42 200 240 8000 10080 9600 B 30 33 800 880 24000 29040 26400 C 60 68 500 480 30000 32640 28800 合计 — — — — 62000 71760 64800 计算三种产品的产量指数和价格指数

产量指数：EqPo-648002=104.52%I.:62000ZqoPo说明报告期与基期相比，三种产品的产量增加了4.52%。ZqiPo-qoP。=64800-62000=2800(千元)说明报告期与基期相比，三种产品的产量增加了4.52%，而使得产值增加了2800000元。价格指数：ZqiPl_ 71760 =110.74%I,一Zqipo64800说明报告期与基期相比，三种产品的价格上涨了10.74%。ZqiP,-ZqiP。=71760-64800=6960（千元）说明报告期与基期相比，三种产品的价格上涨了10.7%，而使得产值增加了6960000元。四、综合指数的应用综合指数的应用很广，在我国和其他各国，都有很多指数采用这种方法计算。下面来考察常用的几个方面。(一)工业产量(产值)指数我国现行统计制度规定，工业总产值按统一规定的不变价格计算。于是，把不同年份的工业总产值对比所确定的动态指标，就是工业产量指数。它是以不变价格为权数（同度量因素）的固定加权综合的指数，用公式表示如下：ZqP,IgZqoP.Pn表示不变价格；qPn表示按不变价格计算的工业总产值。用按不变价格计算的工业总产值来编制工业产量指数，具有如下优点：(1)便于长时期工业产量动态分析，观察工业产值增长变化趋势及其规律性。(2)环比指数数列的连乘积等于定基指数，因而便于定基指数和环比指数之间的相互换算。4

4 产量指数： 104.52% 62000 64800 0 0 1 0 = = =   q p q p I q 说明报告期与基期相比，三种产品的产量增加了4.52%。 q1 p0 −q0 p 0 = 64800 − 62000 = 2800（千元） 说明报告期与基期相比，三种产品的产量增加了4.52%，而使得产值增加了 2800000元。 价格指数： 110.74% 64800 71760 1 0 1 1 = = =   q p q p I p 说明报告期与基期相比，三种产品的价格上涨了10.74%。 q1 p1 −q1 p 0 = 71760 − 64800 = 6960（千元） 说明报告期与基期相比，三种产品的价格上涨了10.7%，而使得产值增加了 6960000元。 四、综合指数的应用 综合指数的应用很广，在我国和其他各国，都有很多指数采用这种方法计算。下面 来考察常用的几个方面。 (一)工业产量(产值)指数 我国现行统计制度规定，工业总产值按统一规定的不变价格计算。于是，把不同年 份的工业总产值对比所确定的动态指标，就是工业产量指数。它是以不变价格为权数(同 度量因素)的固定加权综合的指数，用公式表示如下：   = n n q q p q p I 0 1 pn表示不变价格； qpn表示按不变价格计算的工业总产值。 用按不变价格计算的工业总产值来编制工业产量指数，具有如下优点： (1) 便于长时期工业产量动态分析，观察工业产值增长变化趋势及其规律性。 (2) 环比指数数列的连乘积等于定基指数，因而便于定基指数和环比指数之间的相 互换算

(二)地区物价比较指数前已述及，指数理论主要应用于现象变动的动态研究，但是随着社会经济的发展和科学技术的进步，它已拓展到应用地区之间的综合比较。物价是经济领域中最富有敏感性的现象，因此需要编制物价对比的地区性指数。凡是在企业之间、地区之间甚至国家与国家之间相互比较的指数，都可称为地区性指数。编制地区性指数，人们所关心的是从对比中找出差距，以便挖掘潜力，为领导决策提供依据。因此，在编制物价的地区性指数时，一般以对比基准地区的物量为同度量因素，即编制对比基准地区物量加权综合指数。例如，比较甲乙两个城市全部商品的物价水平，甲城市为对比的城市，乙城市作为对比基准的城市，则物价地区性指数的计算公式为：EqzIp=Zqzpz(三)成本计划完成指数检查成本计划执行情况时，需要编制成本计划完成指数。检查成本计划执行情况，一般有两种不同的要求：一种是检查包括可比产品和不可比产品在内的全部产品成本计划完成情况，在这种场合，直接用计划产量为同度量因素（权数），加权综合求得成本计划完成指数，其计算公式为：Zq.-11. =Zqn-n式中：ZI为报告期实际单位产品成本；zn为计划单位产品成本；qn为计划产量。另一种是检查可比产品成本降低计划完成情况，在这种场合，编制计划时，计划成本指数是在基期的基础上制订的，采用的权数是计划产量。第三节平均指数一、平均指数的概念及与综合指数的关系平均指数是计算总指数的另一种形式，它是在个体指数的基础上计算总指数。在解决复杂总体各组成要素不能直接相加与综合的问题上，平均指数与综合指数是不同的。平均指数是个体指数的加权平均数，它是先计算个体指数，然后将个体指数加权平均而计算的总指数。平均指数和综合指数是计算总指数的两种形式，它们之间既有区别，又有联系。从5

5 (二)地区物价比较指数 前已述及，指数理论主要应用于现象变动的动态研究，但是随着社会经济的发展和 科学技术的进步，它已拓展到应用地区之间的综合比较。物价是经济领域中最富有敏感 性的现象，因此需要编制物价对比的地区性指数。凡是在企业之间、地区之间甚至国家 与国家之间相互比较的指数，都可称为地区性指数。编制地区性指数，人们所关心的是 从对比中找出差距，以便挖掘潜力，为领导决策提供依据。因此，在编制物价的地区性 指数时，一般以对比基准地区的物量为同度量因素，即编制对比基准地区物量加权综合 指数。例如，比较甲乙两个城市全部商品的物价水平，甲城市为对比的城市，乙城市作 为对比基准的城市，则物价地区性指数的计算公式为：   = 乙 乙 乙 甲 q p q p I p (三)成本计划完成指数 检查成本计划执行情况时，需要编制成本计划完成指数。检查成本计划执行情况， 一般有两种不同的要求：一种是检查包括可比产品和不可比产品在内的全部产品成本计 划完成情况，在这种场合，直接用计划产量为同度量因素(权数)，加权综合求得成本计 划完成指数，其计算公式为：   = n n n z q z q z I 1 式中： z1为报告期实际单位产品成本； zn为计划单位产品成本； qn为计划产量。 另一种是检查可比产品成本降低计划完成情况，在这种场合，编制计划时，计划成 本指数是在基期的基础上制订的，采用的权数是计划产量。 第三节 平均指数 一、平均指数的概念及与综合指数的关系 平均指数是计算总指数的另一种形式，它是在个体指数的基础上计算总指数。在解 决复杂总体各组成要素不能直接相加与综合的问题上，平均指数与综合指数是不同的。 平均指数是个体指数的加权平均数，它是先计算个体指数，然后将个体指数加权平均而 计算的总指数。 平均指数和综合指数是计算总指数的两种形式，它们之间既有区别，又有联系。从

区别看，一是在解决复杂总体不能直接同度量问题的思想不同。综合指数是通过引进同度量因素，先计算出总体的总量，然后进行对比，即先综合，后对比。而平均指数是在个体指数的基础上计算总指数，即先对比，后综合。二是在运用资料的条件上不同。综合指数需要研究总体的全面资料，起综合作用的同度量因素的资料要求比较严格，一般应采用与指数化指标有明确经济联系的指标，且应有一一对应全面实际资料，如计算产品实物量综合指数，必须一一掌握各产品的实际价格资料。平均指数则既适用于全面的资料，也适用于非全面的资料。三是在经济分析中的具体作用亦有区别。综合指数的资料是总体的有明确的经济内容的总量指标。因此，总指数除可表明复杂总体的变动方向和程度外，还可从指数化指标变动的绝对效果上进行因素分析。平均指数除作为综合指数变形加以应用的情况外，一般只能通过总指数表明复杂总体的变动方向和程度，而不能用于对现象进行因素分析。平均指数和综合指数的联系主要表现为在一定的权数条件下，两类指数间有变形关系。由于这种变形关系的存在，当掌握的资料不能直接用综合指数形式计算时，则可以用平均指数形式计算，这种条件下的平均指数与其相应的综合指数具有完全相同的经济意义和计算结果。二、平均指数的种类（一）加权算术平均指数1.用综合指数变形权数计算加权算术平均指数。在一定条件下，加权算术平均指数可以是拉氏综合指数的变形。ZqoPoZKgoPo-二oI. =ZqoP。ZqoPoK表示个体物量指数以poqo为权数，加权算术平均指数可以成为综合指数的变形。2.用固定权数计算加权算术平均指数当权数不是综合指数中的poqo，而是某种固定权数W时，称为固定权数加权算术平均指数。W是经过调整计算的一种不变权数，通常用比重表示。这时加权算术平均指数与综合指数不存在变形关系，两者计算结果不会一致。设个体指数为K，固定权数加权算术平均指数的一般表达式为：KWI.=号w6

6 区别看，一是在解决复杂总体不能直接同度量问题的思想不同。综合指数是通过引进同 度量因素，先计算出总体的总量，然后进行对比，即先综合，后对比。而平均指数是在 个体指数的基础上计算总指数，即先对比，后综合。二是在运用资料的条件上不同。综 合指数需要研究总体的全面资料，起综合作用的同度量因素的资料要求比较严格，一般 应采用与指数化指标有明确经济联系的指标，且应有一一对应全面实际资料，如计算产 品实物量综合指数，必须一一掌握各产品的实际价格资料。平均指数则既适用于全面的 资料，也适用于非全面的资料。三是在经济分析中的具体作用亦有区别。综合指数的资 料是总体的有明确的经济内容的总量指标。因此，总指数除可表明复杂总体的变动方向 和程度外，还可从指数化指标变动的绝对效果上进行因素分析。平均指数除作为综合指 数变形加以应用的情况外，一般只能通过总指数表明复杂总体的变动方向和程度，而不 能用于对现象进行因素分析。 平均指数和综合指数的联系主要表现为在一定的权数条件下，两类指数间有变形关 系。由于这种变形关系的存在，当掌握的资料不能直接用综合指数形式计算时，则可以 用平均指数形式计算，这种条件下的平均指数与其相应的综合指数具有完全相同的经济 意义和计算结果。 二、平均指数的种类 （一）加权算术平均指数 1.用综合指数变形权数计算加权算术平均指数。 在一定条件下，加权算术平均指数可以是拉氏综合指数的变形。    = = 0 0 0 0 0 1 0 0 0 0 q p q p q q q p Kq p I q K表示个体物量指数 以p0q0为权数，加权算术平均指数可以成为综合指数的变形。 2.用固定权数计算加权算术平均指数 当权数不是综合指数中的p0q0，而是某种固定权数W时，称为固定权数加权算术平 均指数。W是经过调整计算的一种不变权数，通常用比重表示。这时加权算术平均指数 与综合指数不存在变形关系，两者计算结果不会一致。 设个体指数为K，固定权数加权算术平均指数的一般表达式为：   = W KW I q

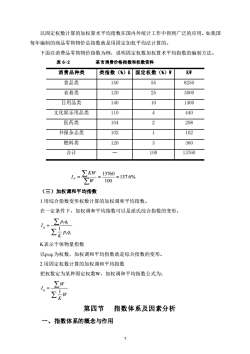
以固定权数计算的加权算术平均指数在国内外统计工作中得到广泛的应用。如我压每年编制的商品零售物价总指数就是用固定加权平均法计算的。下面以消费品零售物价指数为例，说明固定权数加权算术平均指数的编制方法。表 6-2某市消费价格指数和权数资料KW消费品种类类指数（%）K固定权数（%）W15055食品类8250衣着类120253000140101400日用品类4440文化娱乐用品类1102104208医药类1书报杂志类1021023燃料类120360合计10013760EKW13760=137.6%Ip:100Zw（三）加权调和平均指数1.用综合指数变形权数计算的加权调和平均指数。在一定条件下，加权调和平均指数可以是派氏综合指数的变形。Ep1=EpqKK表示个体物量指数以piqi为权数，加权调和平均指数就是综合指数的变形。2.用固定权数计算的加权调和平均指数把权数定为某种固定权数W，加权调和平均指数公式为：Zw-WK第四节指数体系及因素分析一、指数体系的概念与作用7

7 以固定权数计算的加权算术平均指数在国内外统计工作中得到广泛的应用。如我国 每年编制的商品零售物价总指数就是用固定加权平均法计算的。 下面以消费品零售物价指数为例，说明固定权数加权算术平均指数的编制方法。 表 6-2 某市消费价格指数和权数资料 消费品种类 类指数（%）K 固定权数（%）W KW 食品类 150 55 8250 衣着类 120 25 3000 日用品类 140 10 1400 文化娱乐用品类 110 4 440 医药类 104 2 208 书报杂志类 102 1 102 燃料类 120 3 360 合计 — 100 13760 137.6% 100 13760 = = =   W KW I P （三）加权调和平均指数 1.用综合指数变形权数计算的加权调和平均指数。 在一定条件下，加权调和平均指数可以是派氏综合指数的变形。   = 1 1 1 1 1 p q K p q I q K表示个体物量指数 以p1q1为权数，加权调和平均指数就是综合指数的变形。 2.用固定权数计算的加权调和平均指数 把权数定为某种固定权数W，加权调和平均指数公式为：   = W K W I q 1 第四节 指数体系及因素分析 一、指数体系的概念与作用

（一）指数体系的概念由三个或三个以上具有内在联系的指数构成的有一定数量对等关系的整体，叫指数体系。指数体系的形式不是随意的，它是由现象间客观存在的必然联系决定的。例如：商品销售额一商品销售量×商品价格产品产值=产品产量×产品价格上述这些现象在数量上存在的联系，表现在动态变化上，就可以形成如下指数体系：商品销售额指数一商品销售量指数×商品价格指数产品产值指数一产品产量指数×产品价格指数在指数体系中，包括的指数分为两大类：一类是反映现象总变动的指数，通常表现为广义的总指数，这类指数在一个指数体系中只有一个，一般放在算式的左边。另一类是反映某一因素变动的指数，称为因素指数，这类指数在一个指数体系中可以是多个一般放在等式的右边。（二）指数体系的作用1.可以进行因素分析。2.可以进行指数间的互相推算。二、总量指标变动的指数分析(一)总量指标的两因素分析对复杂现象总体的总量指标进行因素分析，要在编制综合指数的基础上进行。例如，要分析多种商品销售额的变动，就要编制出商品销售额指数用来反映总的变动情况，以商品销售量综合指数和商品价格综合指数为因素指数，分别反映销售量和价格两个因素的变动对销售额变动的影响。现仍用表6-1资料进行分析。产品产值指数一产品产量指数X产品价格指数Eqipi_EipoEqp:ZPoZqopoZqipoZqp-Zqopo=(q-Zpo)+(qp-Zqp。)（1）产值指数：ZqiPi_71760115.74%I=Zqopo62000ZqiPi-ZqoP。=71760-62000=9760（千元）8

8 （一）指数体系的概念 由三个或三个以上具有内在联系的指数构成的有一定数量对等关系的整体，叫指数 体系。指数体系的形式不是随意的，它是由现象间客观存在的必然联系决定的。 例如： 商品销售额＝商品销售量×商品价格 产品产值＝产品产量×产品价格 上述这些现象在数量上存在的联系，表现在动态变化上，就可以形成如下指数体系： 商品销售额指数＝商品销售量指数×商品价格指数 产品产值指数＝产品产量指数×产品价格指数 在指数体系中，包括的指数分为两大类：一类是反映现象总变动的指数，通常表现 为广义的总指数，这类指数在一个指数体系中只有一个，一般放在算式的左边。另一类 是反映某一因素变动的指数，称为因素指数，这类指数在一个指数体系中可以是多个， 一般放在等式的右边。 （二）指数体系的作用 1.可以进行因素分析。 2.可以进行指数间的互相推算。 二、总量指标变动的指数分析 (一)总量指标的两因素分析 对复杂现象总体的总量指标进行因素分析，要在编制综合指数的基础上进行。例如， 要分析多种商品销售额的变动，就要编制出商品销售额指数用来反映总的变动情况，以 商品销售量综合指数和商品价格综合指数为因素指数，分别反映销售量和价格两个因素 的变动对销售额变动的影响。现仍用表6-1资料进行分析。 产品产值指数＝产品产量指数×产品价格指数   = 0 0 1 1 q p q p I =   0 0 1 0 q p q p   1 0 1 1 q p q p ( ) ( ) 0 q1 p1 −q0 p0 = q1 p0 −q0 p0 + q1 p1 −q1 p （1）产值指数： 115.74% 62000 71760 0 0 1 1 = = =   q p q p I q1 p1 −q0 p 0 = 71760 − 62000 = 9760（千元）

（2）产量指数：ZqiPo = 64800 =104.52%I=ZqoPo62000ZqiPo-ZqoP。=64800-62000=2800(千元）（3）价格指数：Zqipi_71760=110.74%IP=Zqipo64800ZqiP-ZqiP。=71760-64800=6960(千元)（4）指数体系：115.74%=104.52%×110.74%9760=2800+6960（5）说明：说明三种商品销售额报告期比基期总的增长了11.57%，绝对额增加9760000元，是由于三种商品销售量总的增长了4.52%，使销售额增加2800000元；价格总的上升了10.74%，使销售额增加6960000元两个因素共同作用的结果。显然，本例销售额的增长是销售量和价格两个因素共同增长的结果，其中价格上涨起了主要的作用。(二)总量指标的多因素分析客观现象是比较复杂的，有时某一现象的变动可能要受到三个或三个以上因素的影响。当一个总量指标可以表示为三个或三个以上因素指标的连乘积时，同样可以利用指数体系测定各因素变动对总变动的影响，这种分析就是对总量指标的多因素分析。例如：原材料费用总额=总产量×单位产品原材料消耗量×单位原材料价格qmp=qXm×p在运用多因素分析法时，一定要注意各因素的排列顺序。各因素之间的排列顺序，要符合它们之间相互联系的客观情况，一般是数量指标在前，质量指标在后：各因素的替换必须依据它们之间的客观经济联系，由数量指标到质量指标，按顺序逐次替换。在分析各因素的变动时，可以按综合指数确定同度量因素的一般原则进行，即分析质量指标的变动时将数量指标固定在报告期，分析数量指标的变动时将质量指标固定在基期。根据这个原则，原材料费用总额指数可以分解为由三个指数构成的指数体系。原材料费用总额指数=生产量指数×单位产品原材料消耗指数×单位原材料价格指数9

9 （2）产量指数： 104.52% 62000 64800 0 0 1 0 = = =   q p q p I q q1 p0 −q0 p 0 = 64800 − 62000 = 2800（千元） （3）价格指数： 110.74% 64800 71760 1 0 1 1 = = =   q p q p I p q1 p1 −q1 p 0 = 71760 − 64800 = 6960（千元） （4）指数体系： 115.74% =104.52%110.74% 9760 = 2800+ 6960 （5）说明： 说明三种商品销售额报告期比基期总的增长了11.57%，绝对额增加9760000元， 是由于三种商品销售量总的增长了4.52%，使销售额增加2800000元；价格总的上升了 10.74%，使销售额增加6960000元两个因素共同作用的结果。 显然，本例销售额的增长是销售量和价格两个因素共同增长的结果，其中价格上涨 起了主要的作用。 (二)总量指标的多因素分析 客观现象是比较复杂的，有时某一现象的变动可能要受到三个或三个以上因素的影 响。当一个总量指标可以表示为三个或三个以上因素指标的连乘积时，同样可以利用指 数体系测定各因素变动对总变动的影响，这种分析就是对总量指标的多因素分析。例如： 原材料费用总额=总产量×单位产品原材料消耗量×单位原材料价格 qmp=q×m×p 在运用多因素分析法时，一定要注意各因素的排列顺序。各因素之间的排列顺序， 要符合它们之间相互联系的客观情况，一般是数量指标在前，质量指标在后；各因素的 替换必须依据它们之间的客观经济联系，由数量指标到质量指标，按顺序逐次替换。在 分析各因素的变动时，可以按综合指数确定同度量因素的一般原则进行，即分析质量指 标的变动时将数量指标固定在报告期，分析数量指标的变动时将质量指标固定在基期。 根据这个原则，原材料费用总额指数可以分解为由三个指数构成的指数体系。 原材料费用总额指数=生产量指数×单位产品原材料消耗指数×单位原材料价格指数