南京大学：《高级优化 Advanced Optimization》课程教学资源（讲稿）Lecture 12 Stochastic Bandits - MAB, UCB, linear bandits, self-normalized concentration, generalized linear bandits

NJUAT 南京大学 人工智能学院 SCHOOL OF ARTFICIAL INTELUGENCE,NANJING UNFVERSITY Lecture 12.stochastic bandits Advanced Optimization(Fall 2023) Peng Zhao zhaop@lamda.nju.edu.cn Nanjing University

Lecture 12. Stochastic Bandits Peng Zhao zhaop@lamda.nju.edu.cn Nanjing University Advanced Optimization (Fall 2023)

Outline ·Multi-Armed Bandits Explore-Then-Exploit Upper Confidence Bound ·Linear Bandits ·LinUCB Algorithm Generalized Linear Bandits ·Advanced Topics Advanced Optimization(Fall 2023) Lecture 12.Stochastic Bandits 2

Advanced Optimization (Fall 2023) Lecture 12. Stochastic Bandits 2 Outline • Multi-Armed Bandits • Explore-Then-Exploit • Upper Confidence Bound • Linear Bandits • LinUCB Algorithm • Generalized Linear Bandits • Advanced Topics

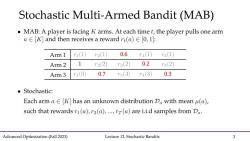
Stochastic Multi-Armed Bandit (MAB) MAB:A player is facing K arms.At each time t,the player pulls one arm a∈[K]and then receives a reward rt(a)∈[O,l: Arm1 1(1) r2(1)】 0.6 r4(1) T5(1) Arm2 1 r2(2) r3(2) 0.2 r5(2) Arm3 r1(3) 0.7 r3(3) r4(3) 0.3 ●Stochastic: Each arm aEK]has an unknown distribution Da with mean u(a), such that rewards ri(a),r2(a),...,rT(a)are i.i.d samples from Da. Advanced Optimization(Fall 2023) Lecture 12.Stochastic Bandits 3

Advanced Optimization (Fall 2023) Lecture 12. Stochastic Bandits 3 Stochastic Multi-Armed Bandit (MAB) Arm 1 Arm 2 Arm 3 0.6 0.7 0.3 1 0.2

Stochastic MAB:Formulation At each round t=l,2,·… (1)the player first chooses an arm at E[K]; (2)and then environment reveals a reward rt(at)e[0,1]; (3)the player updates the model by the pair (at,rt(at)). ·The goal is to minimize the(pseudo小-regret: E[Regretr a)-rdan)) where a*=arg maxeK](a)is the best arm in the sense of expectation. Advanced Optimization(Fall 2023) Lecture 12.Stochastic Bandits 4

Advanced Optimization (Fall 2023) Lecture 12. Stochastic Bandits 4 Stochastic MAB: Formulation • The goal is to minimize the (pseudo)-regret:

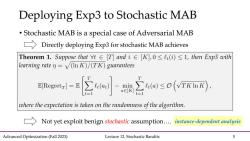
Deploying Exp3 to Stochastic MAB Stochastic MAB is a special case of Adversarial MAB Directly deploying Exp3 for stochastic MAB achieves Theorem1.Suppose that∀t∈[T]andi∈[K],0≤Lt()≤l,then Exp3with learning raten=(In K)/(TK)guarantees EfRegretr=E） where the expectation is taken on the randomness of the algorithm. Not yet exploit benign stochastic assumption....instance-dependent analysis Advanced Optimization(Fall 2023) Lecture 12.Stochastic Bandits 5

Advanced Optimization (Fall 2023) Lecture 12. Stochastic Bandits 5 • Stochastic MAB is a special case of Adversarial MAB Deploying Exp3 to Stochastic MAB Directly deploying Exp3 for stochastic MAB achieves Not yet exploit benign stochastic assumption…. instance-dependent analysis

Regret Decomposition For stochastic MAB,a natural characterization of the arms: (i)Suboptimality gap:Aa=u(a*)-u(a); (ii)Number of times arm a is pulled int rounds:n(a)=>1=a). Regret can be reformulated as no-立=oi-a T E[Regretr)max E =】 ∑(u(a*)-μ(at)nr(a)=∑△anr(a aE[K] a∈[K] Advanced Optimization(Fall 2023) Lecture 12.Stochastic Bandits 6

Advanced Optimization (Fall 2023) Lecture 12. Stochastic Bandits 6 Regret Decomposition • For stochastic MAB, a natural characterization of the arms: • Regret can be reformulated as

A Natural Solution Explore-then-Exploit(ETE): (1)Do explore for the first To round by pulling each arm for To/K times; (2)Do exploit for the rest T-To round by always pulling a=arg maxael]r(a). Theorem1.Suppose that∀t∈[T]anda∈[K],0≤rt(a)≤l,then ETE with exploration period To guarantees eets(段+Tep()a a∈[K1 Advanced Optimization(Fall 2023) Lecture 12.Stochastic Bandits 7

Advanced Optimization (Fall 2023) Lecture 12. Stochastic Bandits 7 A Natural Solution • Explore-then-Exploit (ETE):

Proof of ETE Regret Bound Proof. E[Regretr]=∑△anr(a) aE[K] Exploration Exploitation nT(a)=To/K+(T-To)Pra=a} ≤T/K+(T-To)Pr{m(a)≥(a*)} orm.(a)≤u@ta≤m.(a) 2 snK+r-xwr{ao≥@专aua.o)≤@2"a} 2 snK+T-万(r{.o之uoa}+r{≤专a》 Union bound Pr{XUY}<Pr{X}+Pr{Y} Advanced Optimization(Fall 2023) Lecture 12.Stochastic Bandits 8

Advanced Optimization (Fall 2023) Lecture 12. Stochastic Bandits 8 Proof of ETE Regret Bound Proof.Exploration Exploitation

Proof of ETE Regret Bound Pof间s五/x+T-(r{ma之ota}+pr{aa)sata}》 Hoeffding's inequality.forX&∈[0，l,i∈m,X-a∑1X,we have Pr{x-E[X]≥e}≤exp(-2me2): Pr{X-E[X]≤-c}≤exp(-2me2). →n{a≥o2a}-nmo≥n0+As 2T△8 K △a=4(a*)-(a) 今g4@s(爱+7m(x)》 a∈[K Advanced Optimization(Fall 2023) Lecture 12.Stochastic Bandits 9

Advanced Optimization (Fall 2023) Lecture 12. Stochastic Bandits 9 Proof of ETE Regret Bound Proof

Issue of ETE Theorem1.Suppose that∀t∈[T]anda∈[K],0≤rt(a)≤l,then ETE with explore period To guarantees R≤（假+Tem()a a∈[K ·Need to tune To Tune To with prior of suboptimality gap A:ERegret]=(T) Tune To without prior of suboptimality gap A:E[Regret=O(T2/3) >Solution:do explore and exploit adaptively Advanced Optimization(Fall 2023) Lecture 12.Stochastic Bandits 10

Advanced Optimization (Fall 2023) Lecture 12. Stochastic Bandits 10 Issue of ETE • Need to tune Solution: do explore and exploit adaptively