《电路》课程教学资源（A）习题解答_第12章 三相电路

第12章三相电路 12-1 己知对称三相电路的星形负载阻抗Z=(165+84)2,端线阻抗乙=(2+川2，中线阻抗， 中线阻抗乙w=1+)2,线电压U,=380P。求负载端的电流和线电压，并作电路的相量图 A o 交名食名 c。色。2 a B (C) 题解12-1图 解：按题意可画出对称三相电路如题解12-1图()所示。由于是对称三相电路，可以 归结为一相(A相)电路的计算。如图(6)所示。 220∠0° 1,z+2167+8511744-26.98A 根据对称性可以写出 iB=a2i4=1.174∠-146.98°A ic=aig=1.174∠93.02A 负载端的相电压为 0w=2Zi.=(165+j85)×1.174∠-26.98°=217.90∠0.275

第 12 章 三相电路 12-1 已知对称三相电路的星形负载阻抗 Z = (165 + j84) ，端线阻抗 Z1 = (2 + j1) ，中线阻抗， 中线阻抗 ZN = (1+ j1) ，线电压 U1 = 380V 。求负载端的电流和线电压，并作电路的相量图。 题解 12-1 图 解：按题意可画出对称三相电路如题解 12-1 图（a）所示。由于是对称三相电路，可以 归结为一相（A 相）电路的计算。如图(b)所示。 令 V U U A    0 220 0 3 1 =  =  ，根据图（b）电路有 1.174 26.98 A 167 85 220 0 1     =  − +  = + = Z Z j U I A A 根据对称性可以写出 1.174 146.98 A 2  I  B = a I  A = − 1.174 93.02 A  I  C = aI  B =  负载端的相电压为     U AN = ZI A = (165 + j85)1.174 − 26.98 = 217.900.275

故，负载端的线电压为 0rs=V30∠30°=377.41∠30°V 根据对称性可以写出 Uc=a20rs=377.41∠-90°V Ucr=a0xr=377.41∠150°V 电路的向量图如愿解12-1图（©）所示。 12-2 已知对称三相电路的线电压U=380(电源端)，三角形负载阻抗Z=(4.5+14)2,端 线阻抗乙=(1.5+2)2。求线电流和负载的相电流，并作相量图。 解：本题为对称三相电路，可归结为一相电路计算。先将该电路变换为对称Y一Y电路，如愿解 12-2图(a)所示。图中将三角形负载阻抗Z变换为星型负载阻抗为 乙-7-写45+n40=05+46初n 4是 A'Z c(c + C'Z A(A 60· Zx 30 (a) B(B) (b) 题解12-2图 0三发∠0=220∠0V,根据一相(A相)计算电路（见题解21图(b)中，有线 流i为 1,=Z+z3#667=0084-6578A 220∠0° 根据对称性可以写出

故，负载端的线电压为 3 30 377.41 30 V   U  AB = U  AN =  根据对称性可以写出 377.41 90 V 2  UBC = a U  AB =  − 377.41 150 V  UCA = aU  AB =  电路的向量图如题解 12-1 图（c）所示。 12-2 已知对称三相电路的线电压 U1 = 380V （电源端），三角形负载阻抗 Z = (4.5 + j14) ，端 线阻抗 Z1 = (1.5+ j2) 。求线电流和负载的相电流，并作相量图。 解：本题为对称三相电路，可归结为一相电路计算。先将该电路变换为对称 Y－Y 电路，如题解 12-2 图（a）所示。图中将三角形负载阻抗 Z 变换为星型负载阻抗为 = =  (4.5 + 14) = (1.5 + 4.67)  3 1 3 1 Z Z j j Y 题解 12-2 图 令 V U U A = 0 = 2200 3 1   ，根据一相（ A 相）计算电路（见题解 12-1 图（b）中），有线电 流 A I  为 30.08 65.78 A 3 6.67 220 0 1     =  − +  = + = Z Z j U I Y A A 根据对称性可以写出

in=a2i4=30.08∠-185.78A ic=ad,-30.08∠54.22°A 利用三角形连接的线电流与相电流之间的关系，可求得原三角形负载中的相电流，有 1w=方30=7372-3578A 而 igc=a2irg-17.37∠-155.78°A icx=alrg=17.37∠84.22°A 电路的相量图如题解12-2图(b)所示。 注：从12-1和12-2题的计算分析中可以归纳出Y一Y联结的对称三相正弦交流电路的如下特点： (1)中性点等电位，有U 八=0，中线不起作用，即不管有无中线，电路的情况都一样。 (2)各相具有独立性。即各相的电压和电流只与各相的电源和负载有关，且和各相电源为同相序 的对称量。 由以上特点可以得出计算对称三相电路的一般方法和步骤为： （①)应用△-Y等效变挨（乙，=。，心，-∠-30）把三相电路化为对称的Y-Y联 3 接。 (2)用虚设的、阻抗为零的中线联接中性点，取出一相（一般为A相）电路，计算对应的电压、 电流。 (3)根据对称性，推出其余二相的电压、电流。 需要注意，对称三相电路中电压和电流相值与线值之间的关系，即(1)Y联接中， U,=V30∠30°，i=ih:(2)△联接中，U=Ut,i=V5i4-30°。 12-3 将题12一2中负载Z改为三角形连接（无中线）。比较两种连接方式中负载所吸收的复功率 12-4 图示对称工频三相耦合电路接于对称三相电源，线电压U,=380,R=302,L=0.29H M=0.12H。求相电流和负载吸收的总功率

30.08 185.78 A 2  I  B = a I  A = − 30.08 54.22 A  I  C = aI  A =  利用三角形连接的线电流与相电流之间的关系，可求得原三角形负载中的相电流，有 30 17.37 35.78 A 3 1   I  AB = I  A =  − 而 17.37 155.78 A 2  I  BC = a I  AB =  − 17.37 84.22 A  I  CA = aI  AB =  电路的相量图如题解 12-2 图（b）所示。 注：从 12-1 和 12-2 题的计算分析中可以归纳出 Y—Y 联结的对称三相正弦交流电路的如下特点： （1）中性点等电位，有 0 ' . = NN U ，中线不起作用，即不管有无中线，电路的情况都一样。 （2）各相具有独立性。即各相的电压和电流只与各相的电源和负载有关，且和各相电源为同相序 的对称量。 由以上特点可以得出计算对称三相电路的一般方法和步骤为： （1）应用△－Y 等效变换（ ZY Z△ 3 1 = ，    30 3 =  − AB A U U ）把三相电路化为对称的 Y－Y 联 接。 （2）用虚设的、阻抗为零的中线联接中性点，取出一相（一般为Ａ相）电路，计算对应的电压、 电流。 （3）根据对称性，推出其余二相的电压、电流。 需要注意，对称三相电路中电压和电流相值与线值之间的关系，即（1）Y 联接中，    U1 = 3U ph30 ， ph I I  =  1 ；（2）△联接中， U Uph  =  1 ，    I1 = 3I ph− 30 。 12-3 将题 12—2 中负载 Z 改为三角形连接（无中线）。比较两种连接方式中负载所吸收的复功率。 12-4 图示对称工频三相耦合电路接于对称三相电源，线电压 U1 = 380V ，R = 30，L = 0.29H ， M = 0.12H 。求相电流和负载吸收的总功率

R 题12-4图 解：电路为对称三相电路，去耦等效电路如题解124图所示，可归结为一相(A相)电路来计算。 U=(R+joL-joM)i 令相电压0，为心，-号40=2020，则相电流，为 220/0° 1,R+t-m30+938=3593c-6064 根据对称性可以写出 i。=a2i=3.593∠-180.66°A ic=ad=3.593∠59.34°A 负载吸收的总功率为 P=312R=3×3.5932×30=1161.78W R L-M B。昌5 c。-M m 题解124图 12-5 题12-5图所示对称Y-Y三相电路中，电压表的读数为1143.16V,Z=(15+j153)2, 乙，=0+j2)2。求：(1)图中电流表的读数及线电压UB:(2)三相负载吸收的功率：(3)如果A相的

题 12-4 图 解：电路为对称三相电路，去耦等效电路如题解 12-4 图所示，可归结为一相（A 相）电路来计算。 A A U R j L j M I   = ( +  −  ) 令相电压 U A  为： V U U A = 0 = 2200 3 1   ，则相电流 A I  为 A R j L M j U I A A =  −  +  = + − = 3.593 60.66 30 53.38 220 0 ( )     根据对称性可以写出 3.593 180.66 A 2  I  B = a I  A = − 3.593 59.34 A  I  C = aI  A =  负载吸收的总功率为 P = 3I A 2R = 33.5932 30 =1161.78 W 题解 12-4 图 12-5 题 12-5 图所示对称 Y—Y 三相电路中，电压表的读数为 1143.16V， Z = (15 + j15 3)， Zl = (1+ j2) 。求：（1）图中电流表的读数及线电压 UAB ；（2）三相负载吸收的功率；（3）如果 A 相的

负载阻抗等于零（其他不变），再求(1)(2)：(4)如果A相负载开路，再求(1)(2)。(5)如果加接零 阻抗中性线Z、=0,则(3)、(4)将发生怎样的变化？ A。O马A名 ⊙ A Z B 0 题12-5图 解：图示电路为对称Y一Y三相电路，故有0xw=0,可以归结为一相(A相)电路的计 算。 根据题意知Urg=1143.16,则负载端处的相电压U为 Uw-g-"格6-60v 而线电流为 1=贤-602A(电流表谈数) Z30 故电源端线电压U为 U=U,=V3Z+Zh,=V5×32.232×22=12282V (1)令0w=220∠0V,，则线电流i.为 220/0° Z 故图中电流表的读数为6.14 (2)三相负载吸收的功率为 P=3R=3×6.12×30=3349W (3)如果A相的负载阻抗等于零（即A相短路），则B相和C相负载所施加的电压均为电源线 电压，即N”点和A点等电位，而

负载阻抗等于零（其他不变），再求（1）（2）；（4）如果 A 相负载开路，再求（1）（2）。（5）如果加接零 阻抗中性线 Z N = 0 ，则（3）、（4）将发生怎样的变化？ A A B C N Z Z Z Zl Zl Zl V A' B' C' 题 12-5 图 解：图示电路为对称 Y－Y 三相电路，故有 UNN = 0  ，可以归结为一相（A 相）电路的计 算。 根据题意知 UAB =1143.16V ，则负载端处的相电压 U AN 为 660 V 3 1143.16 3 = = =     A B A N U U 而线电流为 22 A 30 660 1 = = =   Z U I A N （电流表读数） 故电源端线电压 UAB 为 UAB =U1 = 3 Z1 + Z I1 = 3 32.232 22 =1228.2 V (1）令 UAN V   = 2200 ，则线电流 A I  为 6.1 33.69 A 30 20 220 0     = − +  = = Z j U I AN A 故图中电流表的读数为 6.1A。 （2）三相负载吸收的功率为 P = 3I A 2R = 36.1 2 30 = 3349 W （3）如果 A 相的负载阻抗等于零（即 A 相短路），则 B 相和 C 相负载所施加的电压均为电源线 电压，即 N 点和 A 点等电位，而

04B=√30w∠30°=380∠30°V 0c=-0c4=-a0B=380∠-30V 此时三相负载端的各相电流为 受识04-6份A i4=i8+ixx=10.54∠-3.69+10.54∠-63.69 =18.26∠-33.7°A 这时图中的电流表读数变为18.26A。 三相负载吸收的功率变为： P-2ImR=2×(10.54)2×30=6665.5W (4)如果图示电路中A相负载开路，则B相和C相负载阻抗串联接入电压UC中，而 0c=a204B=V3a20w∠30°=380∠-90°V 此时三相负载中的各相电流为 i4=0 =-lcvz 380∠-90° 2x00+205274-12369v 这时图中的电流表读数为零。 三相负载吸收的功率为P=21vR=2×(5,27)2×30=1666.4W 12-6 题12-6图所示对称三相电路中，UAg=380V,三相电动机吸收的功率为1.4kW,其功率因数 1=0.866(滞后)，Z,=-j55Q。求UA和电源端的功率因数

3 30 380 30 V     UAB = UAN =  U AC UCA aU AB V     = − = − = 380 − 30 此时三相负载端的各相电流为 10.54 3.69 A 30 20 380 30     = − +   = = Z j U I AB N B 10.54 63.69 A 30 20 380 30     = − + −  = = Z j U I AC N C 18.26 33.7 A 10.54 3.69 10.54 63.69       =  − I A = INB + INC =  − +  − 这时图中的电流表读数变为 18.26A。 三相负载吸收的功率变为： P = 2I N 2 B R = 2 (10.54) 2 30 = 6665.5 W （4）如果图示电路中 A 相负载开路，则 B 相和 C 相负载阻抗串联接入电压 UBC  中，而 3 30 380 90 V 2 2   U  BC = a U  AB = a U  AN = − 此时三相负载中的各相电流为 I A = 0  V Z j U I I BC BN CN      5.27 123.69 2 (20 20) 380 90 2 = −  +  −  = −  = = 这时图中的电流表读数为零。 三相负载吸收的功率为 P = 2IB 2 NR = 2 (5.27) 2 30 =1666.4 W 12-6 题 12-6 图所示对称三相电路中， UAB = 380V ，三相电动机吸收的功率为 1.4kW，其功率因数  = 0.866 （滞后）， Zl = −j55 。求 UAB 和电源端的功率因数 

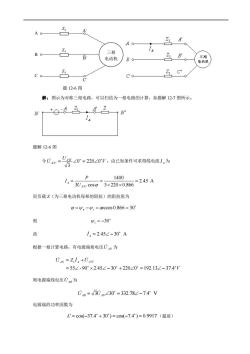
A 三相 电动机 Co 题12-6图 解：图示为对称三相电路，可以归结为一相电路的计算，如题解12-7图所示。 N 题解12-6图 1400 10nsp3x20x086245A P 而负载Z(为三相电动机每相的阻抗)的阻抗角为 0=9.-4,=arccos0.866=30 则 4,=-30 普 i,=2.45∠-30°A 根据一相计算电路，有电源端相电压心八为 Uw =Zi+UoN =55∠-90°×2.45∠-30°+220∠0°=192.13∠-37.4V 则电源端线电压心B为 0=V30w∠30°=332.78∠-7.4V 电源端的功率因数为 =c0s(-37.4°+30)=c0s(-7.4)=0.9917(超前)

A B C Zl Zl Zl A' B' C' 三相 电动机 题 12-6 图 解：图示为对称三相电路，可以归结为一相电路的计算，如题解 12-7 图所示。 题解 12-6 图 令 V U U A B A N    0 220 0 3 =  =      。由已知条件可求得线电流 A I 为 2.45 A 3 220 0.866 1400 3 cos =   = = AN  A U P I 而负载 Z（为三相电动机每相的阻抗）的阻抗角为   = u − i = arccos 0.866 = 30 则   i = −30 故 2.45 30 A  I  A = − 根据一相计算电路，有电源端相电压 U AN  为 V U AN Z I A U A N        55 - 90 2.45 30 220 0 192.13 37.4 1 =    − +  =  − = +   则电源端线电压 UAB  为 3 30 332.78 7.4 V   U  AB = U  AN = − 电源端的功率因数为  = cos(−37.4 + 30 ) = cos(−7.4 ) = 0.9917     （超前）

12-7 图示为对称的Y-△三相电路，UB=380Ψ，Z=(27.5+j47.64)2。求：(1)图中功率表 的读数及其代数和有无意义？(2)若开关S打开，再求(1)。 A。* Bo 题12-7图 解：(1)图示电路中两个功率表的读数分别为 P=RelUn]P=RelUcaic] 则 P+P=RelUni+Ucgic] =ReU,-Ua)i+(Ue-i)i月 =Re⑩i-0a(i+i)+UeiJ =RelUi+Uaia+Ucic]=P 以上表示说明P和B的读数没有什么意义，但P和P的代数和代表了三相电路负载吸收的总功 率，这就是用两个功率表的方法来测量三相功率的原理（称二瓦计法）。 开关S闭合时，图示电路为对称三相制，此时有 P=Re[Ugi]=UaBla cos(WB-Wa) =U,Hcos(wu+30°-44)=U,Hcos(g.+30） B=RelUcaic]=Ucelc cos(Wucs-Vc) =U I cos(wc-30-wic)=U cos(o.-30) 本题中U,=UB=380P,线电流为 1=151=5x 273+476m=1965A 380 阻抗角2.=acam4764=6 27.5 所以两功率表的读数为

12-7 图示为对称的 Y－△三相电路， UAB = 380V ，Z = (27.5 + j47.64) 。求：（1）图中功率表 的读数及其代数和有无意义？（2）若开关 S 打开，再求（1）。 题 12-7 图 解：（1）图示电路中两个功率表的读数分别为 Re[ ] * 1 AB A P U I =   Re[ ] * 2 CB C P U I =   则 U I U I U I P U I U I I U I U U I U U I P P U I U I A A B B C C A A B A C C C A B A C B C AB A CB C = + + = = − + + = − + − + = + Re[ ] Re[ ( ) ] Re[( ) ( ) ] Re[ ] * * * * * * * * * * * 1 2                        以上表示说明 P1 和 P2 的读数没有什么意义，但 P1 和 P2 的代数和代表了三相电路负载吸收的总功 率，这就是用两个功率表的方法来测量三相功率的原理（称二瓦计法）。 开关 S 闭合时，图示电路为对称三相制，此时有 U cos( 30 ) U cos( 30 ) Re[ ] cos( ) 1 1 1 1 * 1     = + − = + = = − uA iA z AB A AB A uAB iA I I P U I U I      U cos( 30 ) U cos( 30 ) Re[ ] cos( ) 1 1 1 1 * 2     = − − = − = = − uC iC z CB C CB C uCB iC I I P U I U I      本题中 U1 =UAB = 380V ，线电流为 11.965 A 275 47.64 380 3 3 2 2 1 = + I = I A I AB =  阻抗角  60 27.5 47.64  z = arctan = 所以两功率表的读数为

W,=P=U,1,cos(p.+30)=380×11.965×cos90°=0 W2=B=U,lc0s(p.-30)=380×11.965×c0s30°=3937.558W 负载吸收的总功率为 P=P+E=3937.558w (2)开关$打开，图示电路变为不对称三相电路，但电源端仍为对称三相电源。故，令 B=380∠30V:仍有Uc=380∠90°，则此时线电流i,和ic为 -i-2691k-0A e=a-27a69160A 380∠90° 这时，两功率表读数为 W1=P=Re[U4B1]=Re[380∠30°×6.91∠30] =380×6.91×c0s60°=1312.9W W2-B=RelUcpic]=Re380∠90°×6.91∠-30] =380×6.91×c0s60°=1312.9W 所以，负载吸收的总功率 P=月+P=2625.8w 注：本题的分析结果说明，在三相三线制电路中，不论对称与否，都可使用二瓦计法来测量三相 功率。需要指出，两个功率表在电路中的联结方式有多种，但必须把其电流线圈串入任意两端线中（本题 为A,C线)，他们的电压线圈的非电源端（无星号*端）共同接到第三条端线上（本题为B线）。在一定的 条件下，两个功率表之一的读数可能为负，求代数和时该读数应取负值 12-8 图示电路，对称三相电源的线电压U=380Ψ，Z=(50+j50)2,Z,=100+100)2,Z, 为R,L,C串联组成，R=502,X2=3142,Xc=-2642。试求：(1)开关S打开时的线 电流：(2)若用二瓦计法测量电源端三相功率，试画出接线图，并求两个功率表的读数(S闭 合时)

W1 = 1 = 1 1 cos( + 30 ) = 38011.965cos90 = 0   z P U I  W2 = P2 =U1 I 1 cos( z − 30 ) = 38011.965cos30 = 3937.558 W 负载吸收的总功率为 P = P1 + P2 = 3937.558 W （2）开关 S 打开，图示电路变为不对称三相电路，但电源端仍为对称三相电源。故，令 380 30 V  U  AB =  ；仍有   UCB = 38090 ，则此时线电流 A I  和 C I  为 6.91 30 A    =  = =  − Z U I I AB A AB 6.91 30 A 27.5 47.64 380 90      =  +  = = = Z j U I I CB C CB 这时，两功率表读数为 380 6.91 cos60 1312.9 W Re[ ] Re[380 30 6.91 30 ] * 1 1 =   = = = =         AB A W P U I 380 6.91 cos60 1312.9 W Re[ ] Re[380 90 6.91 30 ] * 2 2 =   = = = =    −      CB C W P U I 所以，负载吸收的总功率 P = P1 + P1 = 2625.8 W 注：本题的分析结果说明，在三相三线制电路中，不论对称与否，都可使用二瓦计法来测量三相 功率。需要指出，两个功率表在电路中的联结方式有多种，但必须把其电流线圈串入任意两端线中（本题 为 A，C 线），他们的电压线圈的非电源端（无星号*端）共同接到第三条端线上（本题为 B 线）。在一定的 条件下，两个功率表之一的读数可能为负，求代数和时该读数应取负值。 12-8 图示电路，对称三相电源的线电压 U1 = 380V ，Z = (50 + j50)，Z1 = (100 + j100)，ZA 为 R，L，C 串联组成， R = 50， XL = 314， XC = −264 。试求：（1）开关 S 打开时的线 电流；（2）若用二瓦计法测量电源端三相功率，试画出接线图，并求两个功率表的读数（S 闭 合时）

142 c。点 题12-8图 解：(1)标出各线电流参考方向如图所示。开关S打开时，图示电路中 Z,=R+(X,+Xc)=(50+j50)2=Z 所以，此时电路为三相对称电路，有U,w=O,可以归结一相(A相)电路的计算。 令电源端相电压：0N=%=220∠0r,则 方=i,学%-3-的A 根据对称性可以写出 i=im=a2i4=3.11∠-165°A i=ai,=3.11∠75°A B0 12 题解12-10图 (2)开关S闭合时，用二瓦计法测量电源端三相功率的接线图如题解12-10图所示。这时，在A,B 断线之间接入阻抗Z,后，电路为不对称三相电路，但电源仍为对称三相电源。令0w=220∠0V,则 Uaw=220∠-120°V,Ucw=220∠120°V:而04B=380∠30°V,Uc=380∠-90°V, 04c=-·c=-0B=380∠-30V。即，负载Z上的线电压和相电压均未变，则三个负载阻抗Z中的

题 12-8 图 解：（1）标出各线电流参考方向如图所示。开关 S 打开时，图示电路中 Z A = R + j(XL + X C ) = (50 + j50) = Z 所以，此时电路为三相对称电路，有 UNN = 0  ，可以归结一相（A 相）电路的计算。 令电源端相电压： V U UAN   220 0 3 = 1 =  ，则 3.11 45 A 50 50 220 0      = − +   = = = Z j U I I AN A A 根据对称性可以写出 3.11 165 A 2  I  B  = I  B = a I  A =  − 3.11 75 A  I  C  = aI  A =  题解 12-10 图 （2）开关 S 闭合时，用二瓦计法测量电源端三相功率的接线图如题解 12-10 图所示。这时，在 A，B 断线之间接入阻抗 Z1 后，电路为不对称三相电路，但电源仍为对称三相电源。令 UAN V   = 2200 ，则 UBN V   = 220 −120 ，UCN V   = 220120 ；而 UAB V   = 38030 ，UBC V   = 380 − 90 ， UAC UCA aUAB V     = − = − = 380 − 30 。即，负载 Z 上的线电压和相电压均未变，则三个负载阻抗 Z 中的