《电路》课程教学资源（A）习题解答_第6章 储能元件

第6章储能元件 6-2 2F电容上所加电压的波形如图所示。求：(1)电容电流：(2)电容电荷q:(3)电容吸收 的功率p。 ↑u1 tims 题1-8图 解：(1)电压4()的函数表达式为 0 1≤0 10310≤1≤2ms 4-10312≤1≤4ms 0 4≤1ms 根据电容元件u,i的微分关系，得电流i()的函数表达式为： 0 t<0 2×10-30<1<2ms 0=2x1060-0 -2x1032<1<4ms d山 4<tms (2)因为C=,所以有 0 1≤0 2×10-310≤1≤2ms 2×10-6(4-103)2≤1≤4ms q)=Cu()= 0 4≤1ms (3)在电压电流参考方向关联时，电容元件吸收的功率为 0 1≤0 2 0≤1<2ms 2×10-3(4-10302<1<4ms p(0=)i0=〔 0 4≤1ms

第 6 章 储能元件 6-2 2 F 电容上所加电压的波形如图所示。求：（1）电容电流 i；（2）电容电荷 q；（3）电容吸收 的功率 p。 解：（1）电压 u(t) 的函数表达式为         −      = t ms t t ms t t ms t u t 0 4 4 10 2 4 10 0 2 0 0 ( ) 3 3 根据电容元件 u,i 的微分关系，得电流 i(t) 的函数表达式为： =  = − dt du t i t ( ) ( ) 2 10 6         −        − − t ms t ms t ms t 0 4 2 10 2 4 2 10 0 2 0 0 3 3 （2）因为 u q C = ，所以有 q(t) = Cu(t) =          −       − − t ms t t ms t t ms t 0 4 2 10 (4 10 ) 2 4 2 10 0 2 0 0 6 3 3 （3）在电压电流参考方向关联时，电容元件吸收的功率为 p(t) = u(t)i(t) =         −  −      − t ms t t ms t t ms t 0 4 2 10 (4 10 ) 2 4 2 0 2 0 0 3 3

i(t),q(),p()波形如题解1-8图所示。 题解1-8图 注：在图()所示的功率波形中，表示电容吸收功率，处于充电状态，其申压和申指随时间增 加：表示电容供出功率，处于放电状态，其电压和电荷随时间减小。和的两部分面积相等， 说明电 容元件不消耗功率，是一种储能元件。同时它也不会释放出多于它吸收的或储存的能量。所以，电 容是一种无源元件，它只与外部电路进行能量交换。需要指出的是，电感元件也具有这一性质。 6-3 图(a)电容中电流i的波形如图(b)所示现已知4e(0)=0,试求1=1s时，t=2s 和1=4s时的电容电压 1/A (a) 题1-5图 解：己知电容的电流)求电压)时，有 u0=己(5d5+2(55=,)+2∫5d 式中。)为电容电压的初始值 本题中电容电流)的函数表示式为 01≤0 i)={510≤12

i(t), q(t), p(t) 波形如题解 1-8 图所示。 注：在图（c）所示的功率波形中，表示电容吸收功率，处于充电状态，其电压和电荷随时间增 加；表示电容供出功率，处于放电状态，其电压和电荷随时间减小。和的两部分面积相等，说明电 容元件不消耗功率，是一种储能元件。同时它也不会释放出多于它吸收的或储存的能量。所以，电 容是一种无源元件，它只与外部电路进行能量交换。需要指出的是，电感元件也具有这一性质。 6-3 图（a）电容中电流 i 的波形如图（b）所示现已知 uC (0) = 0 ，试求 t = 1 s 时， t = 2 s 和 t = 4 s 时的电容电压。 解：已知电容的电流 i(t) 求电压 u(t) 时，有 0 0 0 0 1 1 1 ( ) ( ) ( ) ( ) ( ) t t t t t u t i d i d u t i d C C C       − = + = +    式中 ( ) 0 u t 为电容电压的初始值。 本题中电容电流 i(t) 的函数表示式为      −     = 10 2 5 0 2 0 0 ( ) t t t t i t

根据u1积分关系，有 1=1s时 0=o0+2名ea =0+5dh=×写r6=125r 1-2s时 ue(2)=ue+di =0+sd=x③r8=5y 1=4s时 e(④=e(2)+2i0ad =5+5-10d=5+5x(-108=-5r 注：电路元件私，i关系的积分形式表明，1时刻的电压与t时刻以前的电流的“全部历史” 有关，即电容有“记忆”电流的作用，故电容是有记忆的元件。因此在计算电容电压时，要关注它 的初始值4（亿，），4.(G,)反映了电容在初始时刻的储能状况，也称为初始状态。电感元件也具有类 似的性质，参见16题。 6-4 图(a)中L=4H,且i,电压的波形如图(b)所示。试求当t=1s,t=2s,t=35 和1=4s时的电感电流i。 012 0/45 a) (b) 题1-6图 解：电感元件弘，i关系的积分形式为 0=iu)+5d5 上式表明，电感元件有“记忆”电压的作用，也属于记忆元件。式中化。)为电感电 流的初始值，反映电感在初始时刻的储能状况。 本题中电感电压的函数表示式为

根据 ui , 积分关系，有 t s =1 时 1 0 1 (1) (0) ( ) C C u u i t dt C = +  tdt t ) 1.25V 2 5 ( 2 1 5 2 1 0 1 0 2 1 0 = + =  =  t = 2 s 时  = + 2 0 ( ) 1 (2) (0) i t dt C uC uC tdt t ) 5V 2 5 ( 2 1 5 2 1 0 2 0 2 2 0 = + =  =  t s = 4 时  = + 4 2 ( ) 1 (4) (2) i t dt C uC uC tdt ( 10t) 5V 2 1 10 5 2 1 5 4 2 4 2 = + − = +  − = −  注：电路元件 ui , 关系的积分形式表明， t 时刻的电压与 t 时刻以前的电流的“全部历史” 有关，即电容有“记忆”电流的作用，故电容是有记忆的元件。因此在计算电容电压时，要关注它 的初始值 u t c ( 0 ) ，u t c ( 0 ) 反映了电容在初始时刻的储能状况，也称为初始状态。电感元件也具有类 似的性质，参见 1-6 题。 6-4 图（a）中 L = 4H ，且 i ，电压的波形如图（b）所示。试求当 t = 1 s ，t = 2 s ，t = 3 s 和 t = 4 s 时的电感电流 i 。 解：电感元件 u,i 关系的积分形式为 0 0 1 ( ) ( ) ( ) t t i t i t u d L = +    上式表明，电感元件有“记忆”电压的作用，也属于记忆元件。式中 ( ) o i t 为电感电 流的初始值，反映电感在初始时刻的储能状况。 本题中电感电压的函数表示式为

0 1<0 100<1<2 u(0= 0 2<1<3 101-403<1<4 0 4<t 应用u,1积分关系式，有 1=1s时，0=o+0h =0+410ct=}x006=25A 1=2s时，2)=0+0h =25+10t=25+7x10f=5A 1=3s时，3)=2)+20d=5+0h=5A 1=4s时，④=3)+20h=5+号打0-40dh=3754 6-5 若已知显像管行偏转线圈中的周期性行扫描电流如图所示，现已知线圈电感为0.01H,电阻略 而不计，试求电感线圈所加电压的波形 ↑1A 200 60 /51 tμs -300c 题1-7图 题解1-7图 解：电流)的函数表达式为 i)= ×101 0<t<60s 3×10(64×106-)60<t<645 根据电感元件4，的微分关系，得电压的函数表达式为

          −        = t t t t t t u t 0 4 10 40 3 4 0 2 3 10 0 2 0 0 ( ) 应用 u,i 积分关系式，有 t = 1 s 时， 1 0 1 i i u t dt (1) (0) ( ) L = +  dt (10t) 2.5 A 4 1 10 4 1 0 1 0 1 0 = + =  =  t = 2 s 时，  = + 2 1 ( ) 1 (2) (1) u t dt L i i 2 1 1 1 2.5 10 2.5 (10 ) 5 4 4 = + = +  = dt t A t = 3 s 时，  = + 3 2 ( ) 1 (3) (2) u t dt L i i 0dt 5 A 4 1 5 3 2 = + =  t = 4 s 时，  = + 4 3 ( ) 1 (4) (3) u t dt L i i 4 3 1 5 (10 40) 3.75 4 = + − = t dt A  6-5 若已知显像管行偏转线圈中的周期性行扫描电流如图所示，现已知线圈电感为 0.01H，电阻略 而不计，试求电感线圈所加电压的波形。 解：电流 i(t) 的函数表达式为       −      = − t t s t t s i t   3 10 (64 10 ) 60 64 10 0 60 60 1.2 ( ) 5 6 6 根据电感元件 u,i 的微分关系，得电压的函数表达式为

m-m2-wecia 4()的波形如题解1-7图，说明电感的电压可以是时间的间断函数。 6-6 电路如图所示，其中R=2,L=1H,C=0.01F,4c(O)=0,若电路的输入电流为： (1)i=2sin21+)4: (2)1=eA。试求两种情况下，当1>0时的u,山，和ue值。 “+ 解：根据R,L和C的u,i关系有 (1)若1=2sim21+)A,则有 4(0-R(0=2×2sim(21+)=4sm21+)/ ()L(-1x2 co2+x2=4cos(2+ 0=4o+2gg=0+0d2s2G+4g=50-10co2+3r (2)若i=eA,则有 4R(0=Ri()=2×eV 0=l0-k(e)=-ey 0=.o+2G6d5=o0ie5=1o-er 6-7 电路如图所示，设,)=U.cos@),1,()=e，试求4，(0和i,)

   −       = = t s t s dt di t u t   3 10 60 64 ( ) 2 10 0 60 ( ) 0.01 3 2 u(t) 的波形如题解 1-7 图，说明电感的电压可以是时间的间断函数。 6-6 电路如图所示，其中 R = 2Ω, L = 1H, C = 0.01F,uC (0) = 0 ，若电路的输入电流为： （1） i t )A 3 π = 2sin( 2 + ； （2） i e A −t = 。试求两种情况下，当 t  0 时的 uR uL , 和 C u 值。 解：根据 R, L 和 C 的 u,i 关系有 （1）若 i t )A 3 π = 2sin( 2 + ，则有 uR t Ri t t t ) V 3 π ) 4sin( 2 3 π ( ) = ( ) = 2 2sin( 2 + = + ( ) ( ) 1 2 cos(2 ) 2 4cos(2 ) 3 3 L di t u t L t t V dt     = =  +  = +     i d d t V C u t u t t C C ) 3 ) 50 100cos(2 3 2sin( 2 0.01 1 ( ) 0 1 ( ) (0) 0 0    = +   = +  + = − +   （2）若 i e A −t = ，则有 u t Ri t e V t R − ( ) = ( ) = 2 ( ) ( ) 1 ( )t t L di t u t L e e V dt − − = =  − = − i d e d e V C u t u t t t C C 100(1 ) 0.01 1 ( ) 1 ( ) (0) 0 0 − − = + = = −       6-7 电路如图所示，设 α t s m s u t U ωt i t Ie − ( ) = cos( ), ( ) = ，试求 ( ) ( ) 2 u t i t L 和 C

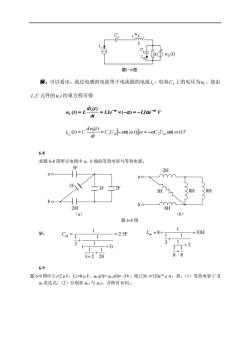
题1-10图 解：可以看出，流过电感的电流等于电流源的电流，电容C,上的电压为4，故由 L,C元件的u,i约束方程可得 ()=L=Lle"x(-a)=-Llaev ie.)-cdu(-CU-so-CU-sionv dt 6-8 求题6-8图所示电路中a、b端的等效电容与等效电感。 ao ao 3H 8H 8H bo 0 (a) (b) 题6-8图 1 C=1 1 -=2.5F L=8+ -=10H 1 1 5 1 3 （1+ *2 3+220 88 69 题6-9图中C1=2μF,C,=8μF:(0(0-5V。现已知=120eHA,求：(1)等效电容C及 (表达式：(2)分别求1与C,并核对KVL

解：可以看出，流过电感的电流等于电流源的电流 s i ，电容 C2 上的电压为 s u ，故由 L,C 元件的 u,i 约束方程可得 LIe LI e V dt di t u t L s t t L     − − = = (− ) = − ( ) ( ) C U  t  C U t V dt d u t i t C m m s C sin( ) sin( ) ( ) ( ) 2 = = 2 −   = − 2  6-8 求题 6-8 图所示电路中 a、b 端的等效电容与等效电感。 a b 3F 2F 20F 1F 5F a b 8H 8H 8H 3H 2H （a） （b） 题 6-8 图 解： 6-9 题 6-9 图中 C1=2μF，C2=8μF；uC1(0)= uC2(0)= -5V。现已知 i=120e-5tμA，求：（1）等效电容 C 及 uC表达式；（2）分别求 uC1 与 uC2，并核对 KVL。 1 2.5F 1 1 5 1 ( 1) 1 1 3 2 20 Cab = = + + + + 1 8 10H 1 1 3 1 2 1 1 8 8 Lab = + = + + +

-0 题69图 解(1)等效电容 ()=uc(+uc2(0)=-10V k4o+己I(5)d5 =-10t1oxl020x0e*d5 10(-15 2) .0r%0r29d5 =-5升2x102010c*d5 1 -5+728xe*k=0-e*v .0r.or3a5 21d =-5+8x- 120 xes6=(-2-3e)V 因此有： uc(t)=uc(t)tucz(t) 6-10 题6-10图中L1=6H,(0F2A:L2=1.5H,h(0=-2A:=6eV,求：(1)等效电感L及1的表达式： (2)分别求h与2，并核对KCL

+ − C1 C2 uC uC1 uC2 i + + − − 题 6-9 图 解（1）等效电容 1 2 1 2 1.6 F C C C C C = =  + uC(0)= uC1(0)+uC2(0)=－10V C C 0 6 5 6 0 5 5 0 1 ( )= (0)+ ( )d C 1 = 10+ 120 10 e d 1.6 10 120 10 e (5 15e )V 1.6 ( 5) t t t t u t u i      − − −   +  = −  −   － － － =－ (2) C1 C1 0 1 6 5 6 0 5 5 0 1 ( )= (0)+ ( )d C 1 = 5+ 120 10 e d 2 10 120 5 e (7 12e )V 2 ( 5) t t t t u t u i      − − −   +  = −  −   － － － =－ C2 C2 0 2 6 5 6 0 5 5 0 1 ( )= (0)+ ( )d C 1 = 5+ 120 10 e d 8 10 120 5 e ( 2 3e )V 8 ( 5) t t t t u t u i      − − −   +  = − −  −   － － － =－ C C1 C2 u t u t u t ( )= ( )+ ( ) 因此有： 6-10 题 6-10 图中 L1=6H，i1(0)=2A；L2=1.5H，i2(0)= -2A；u=6e -2tV，求：（1）等效电感 L 及 i 的表达式； （2）分别求 i1 与 i2，并核对 KCL

-0 题6.10图 解(1)等效电感 锅4or248dg %1m 2*款ed5 6 0yi1(0+2(0)=0V 2+6x7*ek=25-05eh 00+5)d5 60F40r249d5 0d -4 0+127-2e*k=25-25eA 6 *e6=-2eA -2+ i(t)F4十5()

+ − L1 u L2 i i1 i1 题 6-10 图 解（1）等效电感 解(2) i(0)= i1(0)+i2(0)=0V 1 2 1 2 1.2H L L L L L = = + 0 2 0 2 2 0 1 ( )= (0)+ ( )d 1 =0+ 6e d 1.2 6 0 e (2.5 2.5e )A 1.2 ( 2) t t t t i t i u L      − − − +  = −  −   = 2 2 0 2 2 0 2 2 0 1 ( )= (0)+ ( )d 1 = 2+ 6e d 1.5 6 2 e 2e A 1.5 ( 2) t t t t i t i u L      − − − − − +  = −  −   = 1 2 i t i t i t ( )= ( )+ ( ) 因此有： 1 1 0 1 2 0 2 2 0 1 ( )= (0)+ ( )d 1 =2+ 6e d 6 6 2 e (2.5 0.5e )A 6 ( 2) t t t t i t i u L      − − − +  = −  −   =