《电路》课程教学资源（A）习题解答_第4章 电路定理

第4章电路定理 4-1 应用叠加定理求图示电路中电压W6。 1 22 A 329 12/ 题4-图 22 12 22 ①5 sinty 32 120 32e 12 (d 题解4-图 解：首先画出两个电源单独作用式的分电路入题解41图(a)和(b)所示。 对(a)图应用结点电压法可得 1 解得 aSin3sint V 8-1-3m=sm:y 2+1 对(b)图，应用电阻的分流公式有 i=- +动+1359 所以 8=lx1=写e=02ey 故由叠加定理得 uab =ud+u=sint+0.2e V 12 22 12 29 32 12 32 12 () 题解4-图

第 4 章 电路定理 4-1 应用叠加定理求图示电路中电压 ab u 。 解：首先画出两个电源单独作用式的分电路入题解 4-1 图（a）和（b）所示。 对（a）图应用结 点电 压 法可 得 1 5sin ) 2 1 1 3 1 (1 1 t un = + + + 解得 1 5sin 3sin 5 3 n t u t V = = (1) 1 1 1 1 1 3sin sin 2 1 3 3 n ab n u u u t t V =  = =  = + 对（b）图，应用 电阻 的 分流 公 式有 1 1 3 2 1 1 1 1 3 5 t e t i e A − − + =  = + + 所以 (2) 1 1 0.2 5 t t ab u i e e V − − =  = = 故由叠加定理得 (1) (2) sin 0.2 t ab ab ab u u u t e V − = + = +

42 应用叠加定理求图示电路中电压。 -①3 82 109 ①136p 29 题4-图 解：画出电源分别作用的分电路如题解(a)和(b)所示。 对(a)图应用结点电压法有 +0 1 1 1 解得 13.6+5 49=-0.1+0.025+01 18.6248 =82.667V 02253 82 34 ①i36v 102 20 402 22 40 题解4-2图 对(b)图，应用电阻串并联化简方法，可求得 2×8+8￥0」 a=3 8+1840)+2 09r 所以，由叠加定理得原电路的“为 u=0+w9=248-8=80y 331 44 应用叠加定理求(1)图(a)中电压4，(2)图b)中电压U

4-2 应用叠加定理求图示电路中电压 u 。 解：画出电源分别作用的分电路如题解（a）和（b）所示。 对（a）图应用结点电压法有 10 50 8 2 136 ) 10 1 40 1 8 2 1 ( 1 + + + + = + un 解得 (1) 1 13.6 5 0.1 0.025 0.1 n u u + = = + + 18.6 248 82.667 0.225 3 = = = V 对（b）图，应用 电阻 串 并联 化 简方 法 ， 可求 得 10 40 2 (8 ) 10 40 32 16 3 3 (8 ) 2 10 40 18 3 10 40 si u V   + + =  =  =  + + + (2) 16 1 8 2 3 2 3 si u u V − = = −  = − 所以，由叠加定理得原电路的 u 为 (1) (2) 248 8 80 3 3 u u u V = + = − = 4-4 应用叠加定理求(1)图(a)中电压 2 u (2)图(b)中电压 U

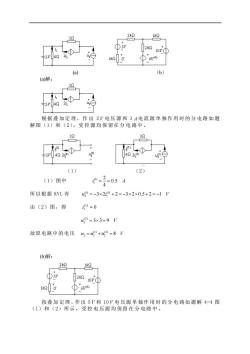
6t) (a) (b) (a)解 根据叠加定理，作出2V电压源和3A电流源单独作用时的分电路如题 解图(1)和(2)。受控源均保留在分电路中。 30 (1) (2) (1)图中 所以根据KVL有 "=-3×20+2=-3×2×0.5+2=-1V 由(2)图，得 2=0 42-3×3-9V 故原电路中的电压，=+2=8V b)解 2 小5 121o① 按叠加定理，作出5V和10V电压源单独作用时的分电路如题解4-4图 (1)和(2)所示，受控电压源均保留在分电路中

(a) （b） (a)解： 根据 叠 加定 理 ，作 出 2 V 电压 源 和 3 A 电流 源 单 独作 用 时的 分 电路 如 题 解图（1）和（2）。受 控 源均 保 留在 分 电 路中 。 （1） （2） （1）图中 (1) 1 2 0.5 4 i A = = 所以根据 KVL 有 (1) (1) 2 1 u i V = −  + = −   + = − 3 2 2 3 2 0.5 2 1 由（2）图，得 0 (2) i 1 = (2) 2 u V =  = 3 3 9 故原电路中的电压 (1) (2) 2 2 2 u u u V = + = 8 (b)解： 按叠 加 定理 ，作出 5 V 和 10 V 电 压源 单 独作 用 时 的分 电 路如 题解 4-4 图 （1）和（2）所示 ， 受控 电 压源 均 保留 在 分 电路 中

2 22 2k (2) 2 ①5 '2w, 3) (4) 应用电源等效变换把图(1)等效为图(3)，图(2)等效为图(4) 由图(3)，得 Uw-2w"-5 1=2Um-5 1+2+子1 从中解得 U0=-3V 0.2U+29 2w+29 由图(d)得 1 2++1 3 20 从中解得 U2= 4 故原电路的电压 U=U四+U2)=-3+4=1V 45 应用叠加定理，按下列步骤求解题4-5图中/，。(1)将受控源参与叠加，画出三个 分电路，第三分电路中受控源电压为61，1，并非分响应，而为未知总响应：(2)求出 三个分电路的分响应、1,1中包含未知量1：(3)利用1。=乃+：+I解出

(1) （2） (3) （4） 应 用 电 源 等效 变 换 把 图 （ 1）等效为图（ 3）， 图 （2）等效为图（4）。 由图（3），得 3 11 (1) 3 2 (1) (1) 2 5 1 1 2 2 5 −  = + + − = U U U 从中解得 (1) U V = −3 由图（d）得 (2) (2) (2) 20 20 2 2 3 3 1 2 11 2 1 3 3 U U U + + =  = + + 从中解得 (2) 20 3 4 11 1 3 U V = = − 故原电路的电压 (1) (2) U U U V = + = − + = 3 4 1 4-5 应用叠加定理，按下列步骤求解题 4-5 图中 a I 。（1）将受控源参与叠加，画出三个 分电路，第三分电路中受控源电压为 6 a I ， a I 并非分响应，而为未知总响应；（2）求出 三个分电路的分响应 a I 、 a I、 a I ， a I 中包含未知量 a I ；（3）利用 a a a a I = I + I + I 解出 a I

10261 36V 12A 62 122 题4-5图 解：(1)将受控源参与叠加，3个分电路如题解4-5图(a入、(b以、(c)所示 36v① 6 00 12 120 题解4-5图 6 2)在分电路(a)中，L-62×124=4 36 在分电路6)中，(=6521： 在分电路⊙)中，上-%· (3)由1，=1。+。+，=4-2+，可解得1，=3A。 4-6 试求图示梯形电路中各支路电流，结点电压和“。其中山，=10V 489.559②4鸟 392122024 ⑩士 题4-5图 解：由齐性定理可知，当电路中只有一个独立源时，其任意支路的响 应与该独立源成正比。用齐性定理分析本题的梯形电路特别有效。现设支 路电流如图所示，若给定 4=6=1A

+ − 6 I a 6I a + − 36V 10 12 12A 题 4-5 图 解：（1）将受控源参与叠加，3 个分电路如题解 4-5 图（a）、(b)、（c）所示 （2）在分电路（a）中， ' 6 12 4 6 12 a I A A =  = + ; 在分电路（b）中， '' 36 2 6 12 a I A = − = − + ； 在分电路（c）中， ''' 6 1 18 3 a a a I I I = = 。 （3）由 ' '' ''' 1 4 2 3 a a a a a I I I I I = + + = − + ，可解得 3 a I A = 。 4－6 试求图示梯形电路中各支路电流，结点电压和 s o u u 。其中 s u ＝ 10V。 解 ： 由 齐 性 定 理可 知 ， 当 电 路 中 只 有 一 个 独 立源 时 ， 其 任 意 支 路 的响 应 与 该 独 立源 成 正 比 。 用 齐 性 定 理 分 析本 题 的 梯 形 电 路 特 别 有 效。 现 设 支 路电流如图所示，若给定 ' 5 5 i i A = =1

则可计算出各支路电压电流分别为 4。=4。=g×20=1×20=20V 42=42=×(4+20)=1x24=24y i4==02/12=24/12=2A 3=1=i+i,=2+1=3A u1=w1=1×5+42=3×5+24=39V 1==+6=1+3=4A 4=,=×4+a1=4×4+39=55V 即当激励4，=4，=55时，各电压、电流如以上计算数值，现给定4，=10V, 相当于将以上激励（缩小了号倍，即K一品 102 故电路各支路的电流和结点电压应同时缩小二倍，有 4=-品4=音=04 M=k=子×39=78y 2 11 2 40 输出电压和激励的比值为= 注：本题的计算采用“倒退法”，即先从梯形电路最远离电源的一端开始，对 电压或电流设一便于计算的值，倒退算至激励处，最后再按齐性定理予以修正。 4-7 图示电路中，当电流源和电压源4反向时(4，不变)，电压4是原 来的0.5倍当i和42反向时(4不变)，电压4是原来的0.3倍。问：

则可计算出各支路电压电流分别为 ' ' 5 ' ' 2 2 5 ' ' 4 4 2 ' ' ' 3 3 4 5 ' ' ' 1 1 3 2 ' ' ' 1 1 2 3 ' ' ' 1 1 20 1 20 20 (4 20) 1 24 24 /12 24 /12 2 2 1 3 5 3 5 24 39 1 3 4 4 4 4 39 55 o o n n n n n n s s n u u i V u u i V i i u A i i i i A u u i u V i i i i A u u i u V = =  =  = = =  + =  = = = = = = = + = + = = =  + =  + = = = + = + = = =  + =  + = 即当 激 励 ' us = us = 55V 时，各 电 压、电流 如 以 上计 算 数值 ，现 给 定 us = 10 V， 相当于将以上激励 ' s u 缩 小了 55 10 倍 ，即 11 2 55 10 K = = 故电路各支路的电流和结点电压应同时缩小 11 2 倍， 有 ' 1 1 ' 2 2 ' 3 3 ' 4 4 ' 5 5 ' 1 1 ' 2 2 ' 2 8 4 0.727 11 11 2 2 1 11 11 2 6 3 11 11 2 4 2 11 11 2 2 1 11 11 2 78 39 11 11 2 48 24 11 11 2 40 20 11 11 n n n n o o i Ki A i Ki A i Ki A i Ki A i Ki A u Ku V u Ku V u Ku V = =  = = = =  = = =  = = =  = = =  = = =  = = =  = = =  = 输出电压和激励的比值为 40 4 11 0.364 10 11 o s u u = = = 注 ： 本题 的 计 算 采用 “ 倒 退 法”， 即 先从 梯 形 电 路 最远 离 电 源 的 一端 开 始 ，对 电压或电流设一便于计算的值，倒退算至激励处，最后再按齐性定理予以修正 。 4－7 图 示 电 路 中 ， 当电 流 源 s1 i 和电压源 s1 u 反向时（ s2 u 不 变）， 电 压 ab u 是 原 来的 0 .5 倍 ；当 s1 i 和 s2 u 反向 时 （ s1 u 不变）， 电压 ab u 是 原 来的 0.3 倍 。问 ：

仅i,反向（41,42均不变)，电压4s应为原来的几倍？ 无源电路 题4-6图 解：根据叠加定理，设响应 ①ub=K1+K4,1+Kg4a 式中K,K2,K为未知的比例常数，将己知条件代入上式，得 ②0.5u=-K1-K41+K4 ③0.3b=-K41+K41-K42 ④x4a=-K1+K241+K,42 将式①，②，③相加，得 同1.86=-K1+K,41+K42 显然⑤式等号右边的式子恰等于式④等号右边的式子。因此得所求倍 数。 x=1.8 注：本题实际给出了应用叠加定理研究一个线性电路激励与响应关系的实验方法。 48 图示电路中U=10V,U2=15V,当开关S在位置1时，毫安表的读数 为1=40m4:当开关S合向位置2时，毫安表的读数为1=-60m4。如果把 开关S合向位置3，毫安表的读数为多少？ 3+△ Ua 题4-7图 解：设流过电流表的电流为【，根据叠加定理

仅 s1 i 反向（ s1 u ， s2 u 均不变 ）， 电 压 ab u 应 为 原来 的 几 倍？ 解 ：根据叠加定理，设响应 ① ab 1 s1 K2us1 K3us2 u = K i + + 式中 K1， K2， K3 为未知的 比 例常 数 ，将 已 知条 件 代 入上 式 ，得 ② 1 1 2 1 3 2 0.5 ab s s s u K i K u K u = − − + ③ 3 1 1 2 1 3 2 0. ab s K us K us u = −K i + − ④ ab 1 s1 K2us1 K3us2 xu = −K i + + 将式①，②，③相 加 ，得 ⑤ 8 1 1 2 1 3 2 1. ab s K us K us u = −K i + + 显 然 ⑤ 式 等 号 右边 的 式 子 恰 等 于 式 ④ 等 号 右 边 的式 子 。 因 此 得 所 求 倍 数。 x =1.8 注 ： 本题 实际 给 出了 应 用叠 加 定理 研 究一 个 线性 电 路激 励 与响 应 关系 的 实验 方 法。 4－8 图示 电 路中 1 10 U V s = ， 2 15 U V s = ，当 开关 S 在 位置 1 时 ，毫 安 表 的读 数 为 ' I mA = 40 ；当 开关 S 合 向位 置 2 时， 毫 安表 的 读 数为 '' I mA = −60 。 如果 把 开关 S 合向位置 3，毫 安表 的 读数 为 多少 ？ 解 ：设流过电流表的电流为 I， 根据 叠 加定 理

I=K 1,+KU, 当开关S在位置1时，相当于U,=0,当开关S在位置2时，相当于 U,=U, 当开关S在位置3时，相当于U,=-U2,把上述条件代入以上方程式中， 可 得关系式 40=K,L, -60=K1,+KU1=40+K2×10 从中解出 10 所以当S在位置3时，有1=Kl,+K,(U2)=40+(-10)x(-15)=190m4 4-9 求图示电路的戴维宁和诺顿等效电路。 手92950里22 A 22 60 1024e 。b (a) (a解： 2 a a 29 42 22 20 6 025A 1) (2) (3) 求开路电压Wc。设w参考方向如图所示，由KVL列方程 (2+4)1+3+2(1-1)=0 解得 4=4×1=4x(-3）=-0.5 求等效内阻R·

1 2 s s I K I K U = + 当开 关 S 在 位置 1 时， 相 当于 Us = 0 ， 当开 关 S 在 位置 2 时 ，相 当 于 Us = Us1， 当开 关 S 在 位置 3 时 ，相 当 于 U U s s = − 2 ，把 上述 条 件 代入 以 上方 程 式中 ， 可 得关系式 60 40 10 40 1 2 1 2 1 − = + = +  = K I K U K K I s s s 从中解出 10 10 100 2 = − − K = 所以当 S 在位置 3 时，有 1 2 2 ( ) 40 ( 10) ( 15) 190 s s I K I K U mA = + = + −  − = 4－9 求图示电路的戴维宁和诺顿等效电路。 (a) (b) (a)解 ： (1) (2) (3) 求开路电压 oc u 。设 oc u 参考方向如图所示，由 KVL 列方程 (2 + 4)I + 3+ 2(I −1) = 0 解得 I A 8 1 = − uoc I ) 0.5V 8 1 = 4 = 4 (− = − 求等效内阻 Req

将原图中电压源短路，电流源开路，电路变为题解4一8(a)图，应用 电阻串并联等效，求得 R=(2+2)/4=22 画出戴维宁等效电路如图(b)所示，应用电源等效变换得诺顿等效电 路如图(c)所示。 其中 -元-950254 注意画等效电路时不要将开路电压u的极性画错，本题设a端为4s的 “+”极性端，求得的u®为负值，故(b)图中的b端为开路电压的实际“+” 极性端。 (b) 1929472222 l62 1024x 1 解：本题电路为梯形电路，根据齐性定理，应用“倒退法”求开路电 压u。设4=W=I0V,各支路电流如图示，计算得 4=4=8=14 n2=42=(2+10)x1=12 i,=i=2=是-244 4=6=+5=2.4+1=3.4A 4a==7×+42=7x3.4+12=35.8y 4=6=4-358-5967A 6 1=+4=5.967+3.4=9.367A 4=4,=9×+4=9×9.367+35.8=120.1V 故当4，=5V时，开路电压4为 5 Me=K=12×10=04160 将电路中的电压源短路，应用电阻串并联等效，求得等效内阻R为 R=[(9∥6+7)∥5+2]110=3.5052

将原 图 中电 压 源短 路，电 流源 开 路，电路 变 为 题解 4－8（a）图，应 用 电阻串并联等效，求得 Req =(2+2)//4=2  画出 戴 维宁 等 效电 路 如图（ b）所 示 ，应 用电 源 等效 变 换得 诺 顿等 效 电 路如图（c）所示 。 其中 A R u I eq oc sc 0.25 2 0.5 = − − = = 注意 画 等效 电 路时 不 要将 开 路电 压 oc u 的极 性 画 错，本题 设 a 端 为 oc u 的 “＋ ”极 性端 ，求 得的 oc u 为 负值 ，故（b）图 中的 b 端 为开 路 电压 的 实际“ ＋” 极性端。 (b) 解 ： 本 题 电 路 为梯 形 电 路 ， 根 据 齐 性 定 理 ， 应用 “ 倒 退 法 ” 求 开 路电 压 oc u 。设 ' 10 oc oc u u V = = ，各支路电 流 如图 示 ，计 算 得 ' 5 5 ' 2 2 ' ' 2 4 4 ' ' ' 3 3 4 5 ' ' 1 1 3 2 ' 1 2 2 ' ' 1 2 3 ' ' 1 1 10 1 10 (2 10) 1 12 12 2.4 5 5 2.4 1 3.4 7 7 3.4 12 35.8 35.8 5.967 6 6 5.967 3.4 9.367 9 9 9.367 35.8 120.1 n n n n n n n s s n i i A u u V u i i A i i i i A u u i u V u i i A i i i A u u i u = = = = = +  = = = = = = = + = + = = =  + =  + = = = = = = + = + = = =  + =  + = V 故当 5 s u V = 时，开路电压 oc u 为 ' 5 10 0.416 12.1 oc oc u Ku V = =  = 将电路中的电压源短路，应用电阻串并联等效，求得等效内阻 R eq 为 [(9 // 6 7) // 5 2]//10 3.505 R eq = + + = 

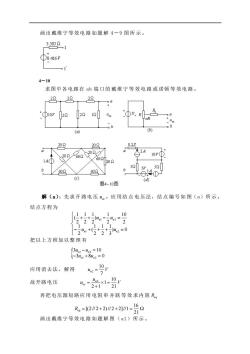
画出戴维宁等效电路如题解4一9图所示。 33051 ①0.416P 4-10 求图中各电路在ab端口的戴维宁等效电路或诺顿等效电路 2222 2212x (a 202 202 028 2A 602 02 40 (c) (d) 题4-10图 解(a):先求开路电压u。应用结点电压法，结点编号如图(a)所示 结点方程为 1 -24+(+2a=0 把以上方程加以整理有 3u.-.,=10 -3l1+84n2=0 应用消去法，解得 a-9r 故开路电压 给1- 再把电压源短路应用电阻串并联等效求内阻R R,=212+22+21=2 画出戴维宁等效电路如题解图(al)所示

画出戴维宁等效电路如题解 4－9 图所示。 4－10 求图中各电路在 ab 端 口的 戴 维宁 等 效电 路 或 诺顿 等 效电 路 。 解（a）：先求开 路电 压 oc u 。应 用结 点 电 压法，结 点 编号 如 图（a）所 示。 结点方程为 1 2 1 2 1 1 1 1 10 ( ) 2 2 2 2 2 1 1 1 1 ( ) 0 2 2 2 3 n n n n u u u u  + + − =   − + + + =  把以上方程加以整理有  1 2 1 2 3 10 3 8 0 n n n n u u u u − = − + = 应用消去法，解得 2 10 7 n u V = 故开路电压 2 10 1 2 1 21 n oc u u V =  = + 再把电压源短路应用电阻串并联等效求内阻 R eq 16 [(2 // 2 2) // 2 2]//1 21 R eq = + + =  画出戴维宁等效电路如题解图（ a1） 所示