《电路》课程教学资源（A）习题解答_第15章 电路方程的矩阵形式

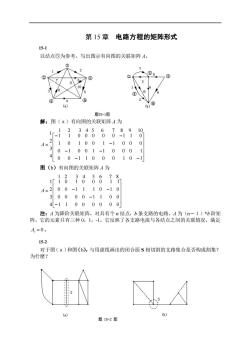
第15章电路方程的矩阵形式 15-1 以结点⑤为参考，写出图示有向图的关联矩阵A。 题15-1图 解：图（日）有向图的关联矩阵A为 -?日886898 0-1001-10001 400-1100010-1 图(b)有向图的关联矩阵A为 可8月88678 A=200-1110-10 30000-1100 4-11000000 注：A为降阶关联矩阵，对具有个n结点，b条支路的电路，A为(n一1)*b阶矩 阵，它的元素只有三种0,1,1，它反映了各支路电流与各结点之间的关联情况，满足 4=0。 15-2 对于图(a)和图(b),与用虚线画出的闭合面S相切割的支路集合是否构成割集？ 为什麽 题15-2图

第 15 章 电路方程的矩阵形式 15-1 以结点⑤为参考，写出图示有向图的关联矩阵 A。 解：图（ａ）有向图的关联矩阵 A 为             − − − − − − − = 0 0 1 1 0 0 0 1 0 1 0 1 0 0 1 1 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 0 0 0 0 0 1 1 0 1 2 3 4 5 6 7 8 9 10 4 3 2 1 A 图（b）有向图的关联矩阵 A 为             − − = − − 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1 1 0 1 0 1 0 1 0 0 0 1 1 4 3 2 1 1 2 3 4 5 6 7 8 A 注：A 为降阶关联矩阵，对具有个 n 结点，b 条支路的电路，A 为（n－１）*b 阶矩 阵，它的元素只有三种 0，1，-1，它反映了各支路电流与各结点之间的关联情况，满足 Ai = 0。 15-2 对于图（ａ）和图（b），与用虚线画出的闭合面 S 相切割的支路集合是否构成割集？ 为什麽？

解：连通图G的一个割集是G的一个支路集合，把这些支路移去，将使G分离为两 部分，但是如果少移去其中一条支路，G仍将连通。对于图（日）和图(b)所示的图 G若把与图示中闭合面S相切割的支路集合移去，图G将分离为三部分，故这些切割的 支路集合不构成割集。 15-3 对于图示有向图，若选支路1,2,3,7为树，试写出基本割集矩阵和基本回路矩 阵：另外，以网孔作为回路写出回路矩阵 .-、03 、4 15-3图 解：图示有向图中，对于所选树(1,2,3,7)的单树支割集（基本割集）组为： Q1,4,8,Q,(2,4,5,6),Q,(3,5,6,8,Q,(7,6,8)分别如图中虚线所示。按先树支后连支的排序 (这种排序是任意的，可以按先连支后树支排序)，可得出基本割集矩阵为 e88&608 g=0,01001-1-10 Q00100-1-11 9:0001001- 对于所选定树(1,2,3,7)的单连支回路（基本回路）组为：1，(41,2)，1，(5,2,3) 1,(6,23,7),1,(81,3,7八，还按先树支后连支的排序，可得出基本回路矩阵为 B,=401100100 011-10010 14-10-110001 以网孔作为回路时，回中组为m,1,2,4),m2(2,3,5),m,(4,6,8),m,(⑤，6,7)，回路方向均 取为顺时针方向，则回中矩阵为

解：连通图 G 的一个割集是 G 的一个支路集合,把这些支路移去，将使 G 分离为两 部分，但是如果少移去其中一条支路，G 仍将连通。对于图（ａ）和图（b）所示的图 G 若把与图示中闭合面 S 相切割的支路集合移去，图 G 将分离为三部分，故这些切割的 支路集合不构成割集。 15-3 对于图示有向图，若选支路 1，2，3，7 为树，试写出基本割集矩阵和基本回路矩 阵；另外，以网孔作为回路写出回路矩阵 解：图示有向图中，对于所选树（1，2，3，7）的单树支割集（基本割集）组为： (1,4,8), (2,4,5,6), (3,5,6,8), (7,6,8) Q1 Q2 Q3 Q4 分别如图中虚线所示。按先树支后连支的排序 （这种排序是任意的，可以按先连支后树支排序），可得出基本割集矩阵为             − − − − − − = 0 0 0 1 0 0 1 0 0 1 0 0 1 1 1 0 1 0 0 1 1 1 0 1 0 0 0 1 0 0 1 1 2 3 4 5 6 7 8 4 3 2 1 Q Q Q Q Qf 对于所选定树（1，2，3，7）的单连支回路（基本回路）组为： (4,1,2), (5,2,3), 1 2 l l (6,2,3,7), (8,1,3,7), 3 4 l l 还按先树支后连支的排序，可得出基本回路矩阵为             − − − − = 1 0 1 1 0 0 0 1 0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 0 1 1 0 0 1 0 0 0 1 2 3 4 5 6 7 8 4 3 2 1 l l l l Bf 以网孔作为回路时，回中组为 (1,2,4), (2,3,5), (4,6,8), (5,6,7), m1 m2 m3 m4 回路方向均 取为顺时针方向，则回中矩阵为

B.=m0-1-10-1000 m00010101 m400001-110 注：Q,为单树支割集矩阵，称基本割集矩阵，Q,中每一个单树支割集的方向为该 树支方向。对一个n个结点、b条支路的电路，Q,为一个(n-1)b的矩阵。它反映了 各个支路电流与基本割集的关联情况，它的元素也只有三种0，-1,1。它满足方程Q1=0, 这也是KCL的矩阵形式。 B,为单连支回路矩阵，称基本回路矩阵，B,中每一个回路的方向为连支方向。对 一个有1个独立回路，b条支路的电路，B,为1*b的矩阵，它反映了支路电压与基本回 路的关系，它的元素也只有0,1,1。满足方程B,“=0,这也是KVL的矩阵形式。 A,B,Q满足关系： AB=0或B,AI=0 B,Q=0或Q,B时=0 要注意A,B,Q,的各列必须按相同支路编号排序。 15-4 对于图示有向图，若选支路1,2,3,5,8为树，试写出基本割集矩阵和基本回路 矩阵 e 题15-4图 解：图示有向图中，对于所选树(1,2,3,5,8)的单树支割集组为：

            − − − − − − = 0 0 0 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 1 0 1 0 0 0 1 1 0 1 0 0 0 0 1 2 3 4 5 6 7 8 4 3 2 1 m m m m Bm 注： Q f 为单树支割集矩阵，称基本割集矩阵， Q f 中每一个单树支割集的方向为该 树支方向。对一个 n 个结点、b 条支路的电路， Q f 为一个（n-1）=b 的矩阵。它反映了 各个支路电流与基本割集的关联情况，它的元素也只有三种 0，-1，1。它满足方程 Q i = 0, f 这也是 KCL 的矩阵形式。 B f 为单连支回路矩阵，称基本回路矩阵， B f 中每一个回路的方向为连支方向。对 一个有 l 个独立回路，b 条支路的电路， B f 为 l *b 的矩阵，它反映了支路电压与基本回 路的关系，它的元素也只有 0，-1，1。满足方程 B u = 0, f 这也是 KVL 的矩阵形式。 A Bf Qf , , 满足关系： = 0 = 0 T f T ABf 或B A = 0 = 0 T f f T Bf Qf 或Q B 要注意 A Bf Qf , , 的各列必须按相同支路编号排序。 15-4 对于图示有向图，若选支路 1，2，3，5，8 为树，试写出基本割集矩阵和基本回路 矩阵。 解：图示有向图中，对于所选树（1，2，3，5，8）的单树支割集组为：

2,(1,4,9,10,22(2,4,9),Q(3.4.6,7),Q,(5,6,7,9,10),Q(8,7,9,10)分别如图中虚线所示，则可得 出基本割矩阵为 12345678910 2「100001001] 00100010010 e=g001001-1100=h,l 0000100-11-1-1 900001001-1-1 0011001000 B,=[Qr:1] 00-1-1-10-1100 -1-101100010 -1001100001 155 对图示有向图，若选结点⑤为参考，并选支路1,2,4,5为树。试写出关联矩阵 基本回路矩阵和基本割集矩阵：并验证B=-4,A和Q,=-B。 2 5 题155图 解：设图示有向图的矩阵A,B,和Q,均按先树支后连支排序，所以有 A=30-111100-4:A 3000-1010 400-100-1 B,=l。00-11010-[B,日小 14-111000

(1,4,9,10), (2,4,9), (3,4,6,7), (5,6,7,9,10), (8,7,9,10) Q1 Q2 Q3 Q4 Q5 分别如图中虚线所示，则可得 出基本割矩阵为 =                 − − − − − − = 0 0 0 0 1 0 0 1 1 1 0 0 0 1 0 0 1 1 1 1 0 0 1 0 0 1 1 1 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 0 0 1 0 0 1 1 1 2 3 4 5 6 7 8 9 10 5 4 3 2 1 Q Q Q Q Q Qf   1t Ql                    − − − − − − − − − − = = 1 0 0 1 1 0 0 0 0 1 1 1 0 1 1 0 0 0 1 0 0 0 1 1 1 0 1 1 0 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 1 0 0 0 0 1 2 3 4 5 6 7 8 9 10 - 1t T 1 B Q  f 15-5 对图示有向图，若选结点⑤为参考，并选支路 1，2，4，5 为树。试写出关联矩阵、 基本回路矩阵和基本割集矩阵；并验证 T t t T Bf = −A A Q = −B − 1 1 1 , 和 。 解：设图示有向图的矩阵 A Bf 和Qf , 均按先树支后连支排序，所以有 =             − − − = − 0 0 1 0 0 1 1 0 0 0 1 0 1 0 0 1 1 1 1 0 0 1 1 0 0 0 0 0 1 2 3 4 5 6 7 4 3 2 1 A   At Al    f t l l l l B = B  1           − − − = 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 1 0 0 1 0 0 1 2 3 4 5 6 7 3 2 1

g,-80100-0-i-k:g1 001001-1 0400010-10 由以上矩阵B,和Q,可得O1=-B。 又因为 「11117T000]「-10-11 -44=0-1-1-1i 00 10 000-i010 0-11 00-1010-1101 0 所以有：B=-AA。 15-6 对图示电路，选支路1,2,4,7为树，用矩阵形式列出其回路电流方程。各支 路电阻均为3V,各电流源电压均为2A。 解：图b)所示有向图中，对所选树(1,2,4,7)的4个单连支(3,5,6,8)的 回路组为：1，(1,2,3,4,12(4,5,7)，(1,2,6,7)，1，(2,4,8)，且其方向为连支方向，如图(b)所示， 则有B=000-110-10 -1-1000110 140-10-10001 R=diag[O,R2.R3.O.Rs,Ro:R3.Rs] Us=[Us 0-Us3 -Usa Uss 00 1s=010015000

  f t l Q Q Q Q Q = 1  Q             − − = − − 0 0 0 1 0 1 0 0 0 1 0 0 1 1 0 1 0 0 1 0 1 1 0 0 0 1 0 1 1 2 3 4 5 6 7 4 3 2 1 由以上矩阵 T Bf Qf Q1 = −Bt 和 ,可得 。 又因为             − − − =             −             − − − − − − = − 0 1 0 0 1 1 1 0 1 1 0 1 0 1 1 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 At A 所以有： 1 1 B At A T t − = − 。 15-6 对图示电路，选支路 1，2，4，7 为树，用矩阵形式列出其回路电流方程。各支 路电阻均为 3V，各电流源电压均为 2A。 解：图(b)所示有向图中，对所选树（1，2，4，7）的 4 个单连支（3，5，6，8）的 回路组为： (1,2,3,4), (4,5,7), (1,2,6,7), (2,4,8), 1 2 3 4 l l l l 且其方向为连支方向，如图（b）所示， 则有             − − − − − − − − − = 0 1 0 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 1 0 1 0 1 1 1 1 0 0 0 0 1 2 3 4 5 6 7 8 4 3 2 1 l l l l B   2 3 5 6 7 8 R = diag 0,R ,R ,0,R ,R ,R ,R   T US = −US1 0 −US3 −US 4 US5 0 0 0   T S S S I = 0 I 2 0 0 I 5 0 0 0

0 6) 题15-6图 将以上各矩阵代入到式BRB'I,=BU,-BR,中可得回路电流方程的矩阵形式为： 「R+R 0 R R2 TIn TUs-Us2+Uss+R:Is2 0 Rs+R-R 0 Uss-Uss-RIs? R -R,R,+R+R, R = R 0 R. R+Rs1 Us+RIs 将已知各参数值代入上式，得 1005 13 010-50 -10 -515 5 13 50510 13 15-7 对图示电路，用运算形式（设零值初始条件）在下列2种不同情况下列出网孔电 流方程：(1)电感L,和L。之间无互感：(2)L,和L。之间有互感M。 题15-7图

将以上各矩阵代入到式 s s T BRB I = BU − BRI 1 中可得回路电流方程的矩阵形式为：             + + − − − + + =                         + − + + + − + 4 2 2 1 2 2 4 5 2 2 1 2 4 2 2 1 4 1 3 1 2 1 1 3 2 2 8 2 7 2 6 7 2 5 7 7 2 3 2 2 0 0 0 0 S S S S S S S S S S S U R I U R I U U R I U U U R I I I I I R R R R R R R R R R R R R R R R R 将已知各参数值代入上式，得             − =                         − − 13 13 10 13 5 0 5 10 5 5 15 5 0 10 5 0 10 0 5 5 14 13 12 11 I I I I 15-7 对图示电路，用运算形式（设零值初始条件）在下列 2 种不同情况下列出网孔电 流方程：（1）电感 L5和L6 之间无互感；（2） L5和L6 之间有互感 M

解：(1)电感L和L之间无互感，若网孔电流方向选取如图(b)所示，则有 123.456 4「-10001 B=201010-1 13001-1-10 11 Z(a)- Uss)=0-Us2s)0000 I,(s)=(s)00000 将以上各矩阵代入到式BZ(s)B'I,(S)=BU,()-Z(s)中，便可得网孔电流方程 的矩阵形式 R+s(L+Le) -sL 「L(s)]「R1(s) 12(s) -U,(s) 11 1(s) 0 -sLg sC3 sC (2)L,和L。之间有互感M,这时，矩阵B,U,(s)和1均不变，只有支路运算阻抗 矩阵有变化，即 [R00000 0R20000 00 000 Z(s)= 000 1 0 0 0000 sLs sM 00 0 0 sM sL 同理，将以上各矩阵代入到网孔电流方程的矩阵形式中，可得 R+s(Ls+Ls+2M) -s(L6+M) -s(Ls+M) I,(s) RIs(s) 1 -s(L6+M) +G+ C+ 1(s)=-2(s) (s) -s(Ls+M) -+sLg 0

解：（1）电感 L5和L6 之间无互感，若网孔电流方向选取如图（b）所示，则有           − − − − = 0 0 1 1 1 0 0 1 0 1 0 1 1 0 0 0 1 1 1 2 3 4 5 6 3 2 1 l l l B       = 5 6 3 4 1 2 , , 1 , 1 ( ) , , sL sL sC sC Z s diag R R   T S S U (s) = 0 −U 2 (s) 0 0 0 0   T s s I (s) = I 1 (s) 0 0 0 0 0 将以上各矩阵代入到式 1 ( ) ( ) ( ) ( ) ( ) S s s T BZ s B I s = BU s − BZ s I 中，便可得网孔电流方程 的矩阵形式           = −                             − − + + − + + − + + − − 0 ( ) ( ) ( ) ( ) ( ) 1 1 1 1 1 ( ) 2 1 1 1 3 1 2 1 1 5 4 3 4 5 4 6 4 6 2 1 5 6 6 5 U s R I s I s I s I s sL sC sC sC sL sC sL sC sL R R s L L sL sL s s （2） L5和L6 之间有互感 M ，这时，矩阵 ( ) , ( ) s s s B U s 和I 均不变，只有支路运算阻抗 矩阵有变化，即                       = 6 5 4 3 2 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 ( ) sM sL sL sM sC sC R R Z s 同理，将以上各矩阵代入到网孔电流方程的矩阵形式中，可得           = −                             − + − + + + − + + + − + + + + − + − + 0 ( ) ( ) ( ) ( ) ( ) 1 1 1 ( ) 1 1 ( ) ( 2 ) ( ) ( ) 2 1 1 1 3 1 2 1 1 5 4 3 4 5 4 6 4 6 2 1 5 6 6 5 U s R I s I s I s I s sL sC sC sM sC s L M sM sC sL sC s L M R R s L L M s L M s L M s S

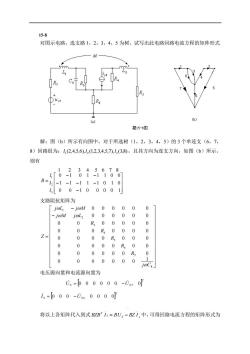
15-8 对图示电路，选支路1,2,3,4,5为树，试写出此电路回路电流方程的矩阵形式 M 题15-8图 解：图(b)所示有向图中，对于所选树(1,2,3,4,5)的3个单连支(6,7， 8)回路组为：1，(2,4,5,6)，12(1,2,3,4,5,7)，1(3,8)，且其方向为连支方向，如图(b)所示， 则有 0子845608 B= 2-1-1-11-1010 400-100001 支路阻抗矩阵为 joL -joM 00000 01 -joM joL2 00000 0 0 0 R000 0 0 0 0 0 Z- 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 000R 0 0 0 00000 电压源向量和电流源向量为 0=b00000-0,0 i=b00-0s40000 将以上各矩阵代入到式BZB'11=BUs-BZI,中，可得回路电流方程的矩阵形式为

15-8 对图示电路，选支路 1，2，3，4，5 为树，试写出此电路回路电流方程的矩阵形式. 解：图（b）所示有向图中，对于所选树（1，2，3，4，5）的 3 个单连支（6，7， 8）回路组为： (2,4,5,6), (1,2,3,4,5,7), (3,8) 1 2 3 l l l ，且其方向为连支方向，如图（b）所示， 则有           − − − − − − − = 0 0 1 0 0 0 0 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 0 0 1 2 3 4 5 6 7 8 3 2 1 l l l B 支路阻抗矩阵为                           − − = 8 7 6 5 4 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 j C R R R R R j M j L j L j M Z      电压源向量和电流源向量为   T US 0 0 0 0 0 0 US 7 0  = −    T S US I 0 0 0 4 0 0 0 0  = −  将以上各矩阵代入到式 S s T BZB I BU BZ I . . 1 . = − 中，可得回路电流方程的矩阵形式为

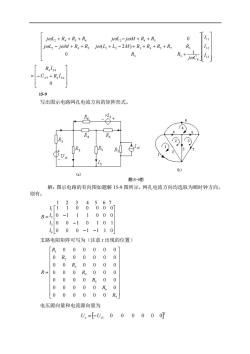
joL2+R,+R+R。 joL:-joM+R+Rs 0 j@L2-j@M+R,+Rs jo(L+L2-2M)+R3+R3+Rs+R3 R 0 R3+- -0,+R,is4 0 15-9 写出图示电路网孔电流方向的矩阵形式。 4 5 ) 题15-9图 解：图示电路的有向图如题解15-9图所示，网孔电流方向均选取为顺时钟方向， 则有： B=40-111000 100-10101 1,000-1-110 支路电阻矩阵可写为（注意「出现的位置） 「R0000001 0R0000 0 00R,0000 R=000R 00 0 0000R0 0000 0 R 0 000000R, 电压源向量和电流源向量为 U,=[-U,4000000

                          + − + + + − + + + + + + + − + + . 1 3 . 1 2 . 1 1 8 3 3 2 4 5 1 2 3 4 5 7 3 2 4 5 6 2 4 5 1 0 ( 2 ) 0 I I I j C R R j L j M R R j L L M R R R R R j L R R R j L j M R R                  = − + 0 7 4 4 4 4 S S S U R I R I    15-9 写出图示电路网孔电流方向的矩阵形式。 解：图示电路的有向图如题解 15-9 图所示，网孔电流方向均选取为顺时钟方向， 则有：             − − − = − 0 0 0 1 1 1 0 0 0 1 0 1 0 1 0 1 1 1 0 0 0 1 1 0 0 0 0 0 1 2 3 4 5 6 7 4 3 2 1 l l l l B 支路电阻矩阵可写为（注意 r 出现的位置）                       = 7 6 5 4 3 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 R R R R R R R R 电压源向量和电流源向量为   T Us = −Us1 0 0 0 0 0 0

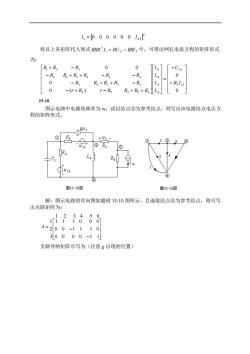
1,=0000001mJ 将以上各矩阵代入到式BRB'I,=BU,-BR、中，可得出网孔电流方程的矩阵形式 为： 「R+R2 -R 0 0 T 「-Usn -R,R,+R+R-R -R 0 0 -R R3+Rs +R -Rs 0 -(r+R4) r-Re R,+Rs+Rol] 0 15-10 图示电路中电源角频率为w,试以结点④为参考结点，列写出该电路结点电压方 程的矩阵形式。 ①R +45 ②R -C1 ①2 题15-10图 题15-10图 解：图示电路的有向图如题材15-10图所示，且选取结点④为参考结点，则可写 出关联矩阵为： 4=200-1110 30000-11 支路导纳矩阵可写为（注意g出现的位置）

  T s S I I = 0 0 0 0 0 0 7 将以上各矩阵代入到式 S S T BRB I = BU − BRI 1 中，可得出网孔电流方程的矩阵形式 为：             − − =                         − + − + + − + + − − + + − − + − 0 0 0 ( ) 0 0 0 7 7 1 1 4 1 3 1 2 1 1 4 5 4 5 6 3 3 5 7 5 2 2 3 4 3 4 1 2 2 s S R I U I I I I r R r R R R R R R R R R R R R R R R R R R 15-10 图示电路中电源角频率为 w，试以结点④为参考结点，列写出该电路结点电压方 程的矩阵形式。 解：图示电路的有向图如题材 15-10 图所示，且选取结点④为参考结点，则可写 出关联矩阵为：           − − = 0 0 0 0 1 1 0 0 1 1 1 0 1 1 1 0 0 0 3 2 1 1 2 3 4 5 6 A 支路导纳矩阵可写为（注意 g 出现的位置）