《电路》课程教学资源（A）习题解答_第7章 一阶电路

·第7章一阶电路 71 图(、(b)所示电路中开关S在1=0时动作，试求电路在1=0，时刻电压、电流的初始值。 S 52 S102 29(t=0) ①1o9=0) 1v① 52 (a) (b) 题7-1图 解：(a)设S在1处闭合的时间已足够，则电路己达稳态，故C开路，4。=10V,即u.(0_)=10V 换路后，S在2处闭合，则有换路定则：L.(0,)=u.(0),C可看作是电压源，于是由KVL 定律： u.(0+)+4,+i(0+)R=0 .(0,)R=-4.(0)-4=-10-5=-15V i(0)=-1.5A 故u.(0)=10Vi.(0)=i0)=-1.5A4(0)=i(0)×R=-15V (b)S在1处闭合，设已达稳态，故L已视短路。 10V 40.)F6+2=1A t=0时刻发生短路，有换路定则得：i0)=i(0)=1A 故在t=0,时刻，L可看作电流源，于是，由欧姆定律： ur(0,)=iz(0)xR=1x5=5V 由KVL定律：u(0,)=-4(0,),故4z(0,)=-5V 7-2 图示各电路中开关S在t=0时动作，试求各电路在1=0，时刻电压、电流。己知图（中的 e0=100sin(om+)V,4.0.)=20V

` 第 7 章 一阶电路 7-1 图 (a)、(b) 所示电路中开关 S 在 t = 0 时动作，试求电路在 t 0 = + 时刻电压、电流的初始值。 +     1 S 2 (t = 0) 10V  + 5V 10 C 2F uc +  ci +  10V    1 S 2 (t = 0) +  L 1H uL 5 Li  5 （a） (b) 题 7-1 图 解：(a)设 S 在 1 处闭合的时间已足够，则电路已达稳态，故 C 开路， uc =10V ，即 uc (0 ) =10V 换路后， S 在 2 处闭合，则有换路定则： (0 ) (0 ) uc + = uc  ，C 可看作是电压源，于是由 KVL 定律： uc (0+ ) + us + i c (0+ )R = 0 i c (0+ )R = uc (0 )  us = 10  5 = 15V i c (0+ ) = 1.5A 故 uc (0+ ) =10V i c (0+ ) = i(0+ ) = 1.5A uR (0+ ) = i(0+ )R = 15V (b) S 在 1 处闭合，设已达稳态，故 L 已视短路。 ( ) 1A 5 5 10V (0 ) = +  i L  = t = 0 时刻发生短路，有换路定则得： iL (0+ ) = iL (0 ) = 1A 故在 = 0+ t 时刻， L 可看作电流源，于是，由欧姆定律： uR (0+ ) = i L (0+ )R =15 = 5V 由 KVL 定律： (0 ) (0 ) uR + = uL + ，故 uL (0+ ) = 5V 7-2 图示各电路中开关 S 在 t = 0 时动作，试求各电路在 t 0 = + 时刻电压、电流。已知图(d)中的 ( ) 100sin( ) 3 e t t  = +  V ， (0 ) 20 c u  = V

32 D20V☐ 2F 3A S309 -S 9202 15 10H 32 (a) 6 159g 30V 52 10V①252 0.1uF (c) (d) 题7-2图 解：(1)对图7-2()电路，在换路前两个电容相当于开路，可求的两个电容电压为 4(0_)= 3+6+3*3N=5v 20 4(0)= 3+6+3*6V=10v /20 在t=0,时，两个电容均用电压源代替，则t=0,时的等效电路如图7-2(a')所示，其中 4(0,)=4(0)=5V,42(0)=山2(0)=10V。可解出各初始值为 i(0)=4/3A,i2(0)=1A,i0)=7/3A 32 0)30 、i0) -2F 20V 32 4o.)①s13 图7-2(a) 图7-2(a') (2)对图7-2(b)电路，在换路前电感相当于短路，可求得 20 6 i(0_)=3× ×20+30A=号A 在t=0,时，电感元件用电流为(0，)=(0)=6/5A的电流源代替，则t=0,时的等效电路 如图7-2(b')所示，解得 (0,)=3A,(0)=-l5i0)=-18V,4(0)=-3+15(0)=-21.6V

+  20V 3   6  2F 1F 3   S 3A   20    2 1 S 15 30 10H (a) (b) +  30V 15   S +  10V 5   25 1F +    +  20 e(t) S (0 ) uc  0.1F (c) (d) 题 7-2 图 解：(1)对图 7-2 (a)电路，在换路前两个电容相当于开路，可求的两个电容电压为 3 V 5V 3 6 3 20 (0 ) 1  =       + + u  = 6 V 10V 3 6 3 20 (0 ) 2  =       + + u  = 在 = 0+ t 时，两个电容均用电压源代替，则 = 0+ t 时的等效电路如图 7-2 ( a )所示，其中 u1 (0+ ) = u1 (0 ) = 5V ，u2 (0+ ) = u2 (0 ) =10V 。可解出各初始值为 i 1 (0+ ) = 4 3A ， i 2 (0+ ) =1A ，i(0+ ) = 7 3A +  20V 3   6  2F 1F 3   S +  20V 3   6  3   S (0 ) u2 + (0 ) u1 + (0 ) + i (0 ) 2 + i(0 ) 1 + i 图 7-2（a） 图 7-2 ( a ) (2)对图 7-2（b）电路，在换路前电感相当于短路，可求得 A 5 6 A 20 30 20 (0 ) 3  =      + iL  =  在 = 0+ t 时，电感元件用电流为 i L (0+ ) = i L (0 ) = 6 5A 的电流源代替，则 = 0+ t 时的等效电路 如图 7-2 ( b )所示，解得 i 1 (0+ ) = 3A ， u(0+ ) = -15i L (0+ ) = 18V ，uL (0+ ) = (3+15)i L (0+ ) = 21.6V

S302 32 3A o 202 10H 一202 15 图7-2(b) 图7-2b') (3)对图7-2（©）电路，在换路前电容相当于开路，求出 4.(0)= 30-10x5+10V=15V 15+5 在t=0,时，电容用电压为u.(0,)=4.(0)=15V的电压源代替，作出t=0,时的等效电路如 图7-2(c')所示，可求得 1.0.)=10-40-1 25+5 1 40,)=-1.0,)=6A 152 中w5n@)bo )30V 10W 10VD250 0) 图7-2(c)》 图7-2(c') (4)对图7-2(d)电路，在1=0.时，将电容用电压为u.(0.)=4,(0_)=20V的电压源代替 得1=0，时的等效电路如图7-2(d')所示，其中电源(0.)的值为 e0.)-（10sn9V=866v 可求出 .0,)=e0,)w.0=3.3A 20 u(0,)=20i.(0,)=66.6A 202 0) u0)厂 De(0. ①Du(0.) 图7-2(d) 图7-2(d) 7-3 电路如图所示，开关未动作前电路已达稳态，t=0时开关S打。求

3A   20    2 1 S 15 30 10H 3A 20 15  3  + -( ) L 0+ u ( ) 0+ u + - ( ) L 0+ i ( ) 1 0+ i 图 7-2（b） 图 7-2( b ) (3)对图 7-2（c）电路，在换路前电容相当于开路，求出 5 10 V 15V 15 5 30 10 (0 )  =       + +  uc  = 在 = 0+ t 时，电容用电压为 uc (0+ ) = uc (0 ) =15V 的电压源代替，作出 = 0+ t 时的等效电路如 图 7-2 ( c )所示，可求得 A 6 1 25 5 10 (0 ) (0 ) =  +  = + + c c u i A 6 1 (0 ) (0 ) i 1 + = i c + = +  30V 15   S +  10V 5   25 1F +  30V 15  +  10V 5  25 +  ( ) u c 0 + ( ) u c 0 + ( ) 1 0 + i 图 7-2（c） 图 7-2 ( c ) (4)对图 7-2（d）电路， 在 = 0+ t 时，将电容用电压为 uc (0+ ) = uc (0 ) = 20V 的电压源代替， 得 = 0+ t 时的等效电路如图 7-2 ( d )所示，其中电源 (0 ) + e 的值为 V 86.6V 3 (0 ) 100sin  =      + =  e 可求出 3.33A 20 (0 ) (0 ) (0 ) =  = + + + c c e u i u(0+ ) = 20i c (0+ ) = 66.6A +    +  20 e(t) S (0 ) uc  0.1F +  +  20  + ( ) u c 0 + ( ) u 0 + ( ) 0 + e ( ) c 0 + i 图 7-2（d） 图 7-2 ( d ) 7-3 电 路 如 图 所 示 ， 开 关 未 动 作 前 电 路 已 达 稳 态 ， t=0 时开关 S 打。求

0M盘· 解：这是一个求二阶电路初始值的问题，求法与一阶电路类似。先求4(O_)和 i,(0)。t<0时，电路处于稳态，把电容断开，电感短路，电路如题解图(a)所示。由 图(a)得 40.)=2x3-2x3-6v 6∥6+36 40.)=g-92A 3 根据电容电压和电感电流的连续性，得 4c(0,)=uc(0_)=6V z(0.)=iz(0)=2A 0.1H - ①12V 132 24 卡uc 题71图 画出0，等效电路如题解图(b)所示。由图(b)可求得 10.)=12-0-12-6-1A 6 6 c0、=0,)=40,-0,=1-2=- -40-24Ws C 24

0 0 0 (0 ), (0 ), , , C L R C L du di di u i dt dt dt + + + + + 。 解：这是一个求二阶电路初始值的问题，求法与一阶电路类似。先求 (0 ) uC  和 (0 ) L  i 。t<0 时，电路处于稳态，把电容断开，电感短路，电路如题解图（a）所示。由 图（a）得 6 V 6 12 3 6 // 6 3 12 3 (0 ) =  = +  uc  = 2 A 3 6 3 (0 ) (0 ) = = =   C L u i 根据电容电压和电感电流的连续性，得 uC (0+ ) = uC (0 ) = 6 V i L (0+ ) = i L (0 ) = 2 A 画出 + 0 等效电路如题解图（b）所示。由图（b）可求得 1 A 6 12 6 6 12 (0 ) (0 ) =  =  = + + C R u i 0 = (0+ ) = (0+ )  (0+ ) = 1 2 = 1 + C R L C i i i dt du C 24 24 1 (0 ) 1 0 =   = = + + C i dt duC C V/s

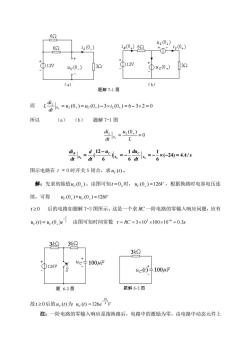
4z(0,) iz(0) x(0,)62 iz(0,) 0+ ①D12V ①12W 4c(0_) ①uc(0,) 3 9 (a) (b) 题解7.1图 面年lk=0.)0.)-3x0,)=6-3x2=0 所以 (a) (b)题解7-1图 k=”0-0 L =g。=g=训=w: 图示电路在t=0时开关S闭合，求uc(t)。 解：先求初始值(0，)。由图可知t=0.时，uc(0.)=126P,根据换路时电容电压连 续，可得 u(0.)=uc(0_)=126V 1≥0后的电路如题解7-3图所示。这是一个求C一阶电路的零输入响应问题，应有 4e)=4e(0,)e由图可知时间常数r=RC=3×102×100×106=0.35 3kQ 3k 32 uc号100uF ①126V uc()片1004F 题6.3图 题解6-3图 故1≥0后的e(0)为，0=126e当v 注：一阶电路的零输入响应是指换路后，电路中的激励为零，由电路中动态元件上

而 0 = (0+ ) = (0+ )  3 (0+ ) = 6  3 2 = 0 + L C L L u u i dt di L 所以 （a） （b） 题解 7-1 图 0 (0 ) 0 = = + + L u dt diL L A s dt u du dt d dt diR C C ( 24) 4 / 6 1 6 1 ) 6 12 ( 0 0 =  0 =    =  = + + + 图示电路在 t = 0 时开关 S 闭合，求 u (t) C 。 解：先求初始值 (0 ) uC + 。由图可知 = 0 t 时， uC (0 ) =126V ，根据换路时电容电压连 续，可得 (0 ) uC + = uC (0 ) =126V t  0 后的电路如题解 7-3 图所示。这是一个求 RC 一阶电路的零输入响应问题，应有 uC (t) =  t C u e  + (0 ) 由图可知时间常数 RC 3 10 100 10 0.3s 3 6 = =    =   故 t  0 后的 u (t) C 为 u (t) C e V t 3 10 126  = 注：一阶电路的零输入响应是指换路后，电路中的激励为零，由电路中动态元件上

的初始储能产生的响应，它是电路的齐次微分方程满住初试条件的解。若零输入响应用 ∫)表示，其初始值为f(0,),则零输入响应可表示为 L.()=1(0.)e t>0 上式可以作为公式直接应用如本题的求解。 7-4 开关S原在位置1己久，t0时合向位置2，求c()和()。 1 100k2 -100k2 10μF 解：1>0时的电路如题解7-4图(a)所示。 25Q2 ①5w 1002 uc(0_) 100a 104F (a) (b) 题解6.4图 由图可知 5 .0.)=100+25×100=4 故可得电容电压的初始值 4c(0,)=(0.)=4 1>0后的电路如题解图(b)所示，这是一个一阶RC零输入电路。由于从电容两端看去的等效电阻 为R=100∥100=50k2 故有时间常数r=RC=50x10×10x10=之9 电容电压 uc(t)=uc(0.)e :=4e-2V 电流 0=9-0o4em4

的初始储能产生的响应，它是电路的齐次微分方程满住初试条件的解。若零输入响应用 f (t) x 表示，其初始值为 (0 ) x + f ，则零输入响应可表示为  t x x f t f e  = + ( ) (0 ) t  0 上式可以作为公式直接应用如本题的求解。 7-4 开关 S 原在位置 1 已久，t=0 时合向位置 2，求 u (t) C 和 i(t) 。 +  5V 25k 100k +  uc 10F    1 2 S    100k i 解：t > 0 时的电路如题解 7-4 图（a）所示。 由图可知 uC 100 4V 100 25 5 (0 )  = +  = 故可得电容电压的初始值 uC (0+ ) = uC (0 ) = 4V t > 0 后的电路如题解图（b）所示，这是一个一阶 RC 零输入电路。由于从电容两端看去的等效电阻 为 R0 =100//100 = 50k 故有时间常数 R C s 2 1 50 10 10 10 3 6 = 0 =    =   电容电压 u t u e e V t t C C 2 ( ) (0 ) 4   = + =  电流 e mA u t i t C 2t 0.04 100 ( ) ( )  = =

7-5 图中开关S在位置1已久，1=0时合向位置2，求换路后的i(t)和4，(t)。 12 +wL- ①10v 42 42 题6-5图 解：1>0时的电路如题图解(a)所示。 由图(a)可知 10 0)=+424 根据换路时i,不能跃变，有 i(0.)=i(0.)=2A >0后的电路如图(b)所示。这是一个一阶RL零输入电路。其时间常数为 L11 7=R4+489 故电感电流和电压分别为 i(t)=i(t)=i(0.)e=2eA 4,0=L亚=1x2e"x-8)=-16e*p d 也可利用KVL计算u,(),即 4()=-(4+4),()=-16ev 注：从7-3到75题的求解过程可以归纳出一阶电路零输入响应的步骤为：(1)由1=0的电路确定 电容电压4c(0)或1，(0_)电感电流，根据c(0,)=4c(0),z(0)=z(0)得出动态元件的初始值： ②)求1>0后电路的时间常数T,对RC电路有T=RC,对RL电路有7，式中飞为动态 元件两端看去的一端口电路的等效电阻，计算R,的方法与求戴维宁等效电阻的方法相同：(3)利用 c(I)=ue(0,)er或i,()=iz(0,)er,求得4e()和i,),再利用KCL或KL元件的伏安关系

7-5 图中开关 S 在位置 1 已久，t = 0 时合向位置 2，求换路后的 i(t) 和 u (t) L 。 解：t > 0 时的电路如题图解（a）所示。 由图（a）可知 i L 2A 1 4 10 (0 ) = +  = 根据换路时 L i 不能跃变，有 i L (0+ ) = i L (0 ) = 2A t>0 后的电路如图（b）所示。这是一个一阶 RL 零输入电路。其时间常数为 s R L 8 1 4 4 1 = +  = = 故电感电流和电压分别为 i t i t i e e A t t L L 8 ( ) ( ) (0 ) 2   = = + =  e e V dt di u t L L t t L 8 8 ( ) 1 2 ( 8) 16   = =    =  也可利用 KVL 计算 u (t) L ，即 8 ( ) (4 4) ( ) 16 t L L u t i t e V  =  + =  注：从 7-3 到 7-5 题的求解过程可以归纳出一阶电路零输入响应的步骤为：（1）由 t 0 =  的电路确定 电容电压 (0 ) C u  或 (0 ) L i  电感电流，根据 (0 ) C u + = (0 ) C u  , (0 ) (0 ) L L i i +  = 得出动态元件的初始值； （2）求 t  0 后电路的时间常数  。对 RC 电路有 R C0  = ，对 RL 电路有 0 L R  = ，式中 R0 为动态 元件两端看去的一端口电路的等效电阻，计算 R0 的方法与求戴维宁等效电阻的方法相同；（3）利用 ( ) (0 ) t C C u t u e   = + 或 ( ) (0 ) t L L i t i e   = + ，求得 () C u t 和 () L i t ，再利用 KCL 或 KVL 元件的伏安关系

式求出其它各支路的电压和电流。也可根据0等效电路，求出其它待求量的初值，应用 ()=f(0.)er得到所求量 7-6 图示电路中，若0时开关S闭合，求电流1。 0.1H 20uF YY m 0.11 i 20F 1002 1002s〉 01002 11502 150g2 1002 60 60v 题7-6图 解：设t0时，仍然为一阶零输入回路： RC回路：4.=4.(0，)e=24e0rV RL回路：1=，0，e兰-024emA 由于10=C,@20×10-×24×仁500y0mA=-0.24e0A d 因此，由KCL定律：i=-,()-i.()=0.24e6o-e-1omA 7-9 图示电路中，若1=0时开关S打开，求4和电源发出的功率

式求出其它各支路的电压和电流。也可根据 0+ 等效电路，求出其它待求量的初值，应用 ( ) (0 ) t x x f t f e   = + 得到所求量 7-6 图示电路中，若 t=0 时开关 S 闭合，求电流 i。 +  100 150 60V 100 0.1H 20F S i   题 7-6 图 解：设 t<0 时，S 打开且保持足够长的时间，因此，电路已达稳态，有 L 短路，C 开路，见图 7-5（a）。 +  100 150 60V 100   ( ) ( ) u c 0 L 0 i +  +  100 150 60V 100 0.1H 20F i   u c L i c i 图 7-5（a） 图 7-5（b） 于是，由 KVL 定律 0.24A 150 100 60 (0 ) = + iL  = uc (0 ) = 60V  150 iL (0 ) = 60V  36V = 24V t = 0 时， S 闭合，发生换路，电路如图 7-5（b）所示，由换路定则有 i L (0+ ) = i L (0 ) = 0.24A，uc (0+ ) = uc (0 ) = 24V 由于短路， L 和 C 分别组成互不相关的回路，因此，在 t  0 时，仍然为一阶零输入回路： RC 回路： (0 ) 24 V RC 500t t c c u u e e   = + = RL 回路： (0 ) 0.24 A 1000t t L R L L i i e e   = + = 由于 ( ) 20 10 24 ( 500) A 0.24 A ( ) c 6 500t 500t c e e dt du t i t C    =     =  因此，由 KCL 定律： ( ) ( ) 0.24( )A 500t 1000t L c i i t i t e e   =   =  7-9 图示电路中，若 t = 0 时开关 S 打开，求 C u 和电源发出的功率

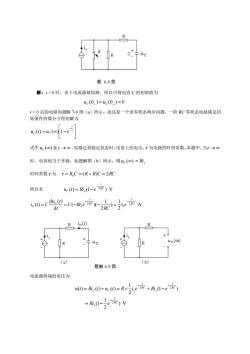
cT卡uc 题6-9图 解：1>0时，由于电流源被短路，所以可得电容C的初始值为 c(0,)=4c(0)=0 1>0后的电路如题解7-9图()所示。故这是一个求零状态响应问愿。一阶RC零状态电路满足初 始条件的微分方程的解为 4e0=e(m1-e] 式中4c(0)是t→0，电路达到稳定状态时，电容上的电压，t为电路的时间常数。本题中，当1→0 时，电容相当于开路，如题解图(b)所示，则4(o)=， 时间常数t为T=RC=(R+R)C=2RC 所以有 uc(t)=Ri,(1-eZRC)V 0=c-C-e产X-)e产A dt +0 R R uc(co) 〔a) (b) 题解6-9图 电流源两端的电压为 0=风e0+e0=Rx之，e壶+危，0-e)

解：t > 0 时，由于电流源被短路，所以可得电容 C 的初始值为 uC (0+ ) = uC (0 ) = 0 t > 0 后的电路如题解 7-9 图（a）所示。故这是一个求零状态响应问题。一阶 RC 零状态电路满足初 始条件的微分方程的解为       =     t C C u (t) u ( ) 1 e 式中 () uC 是 t → ，电路达到稳定状态时，电容上的电压，  为电路的时间常数。本题中，当 t → 时，电容相当于开路，如题解图（b）所示，则 () uC = Ris 时间常数  为  = R0C = (R + R)C = 2RC 所以有 ( ) (1 2RC ) V t C s u t Ri e  =  A 2 1 ) 2 1 ( )( d d ( ) ( ) 2 2RC t s RC t s C C i e RC C Ri e t u t i t C   = =   = 电流源两端的电压为 ) V 2 1 (1 (1 ) 2 1 ( ) ( ) ( ) 2 s 2 2 RC t RC t s RC t C C s Ri e u t Ri t u t R i e Ri e    =  = + =  + 

则电流返发出的功率为P=,)=0-)e证)W 7-10 图示电路中开关S闭合前，电容电压c为零。在t=0时S闭合，求t)0时的c() 和ie(0 10k2 5 (t=0) 102 209 10zF÷4c 解：由题意可知：4(0)=Wc(0.)=0,这是一个求零状态的问题。在1→o时电路 如题解7-10图所示。 102 52 4c(o) 由图可得 20 4e.(o)=10+10×10=10V 等效电阻R。=[10/10)+5]=10k2 所以时间常数 RC-10x10x10x10 则t>0时，电容电压 4e(0=ae(ol-ei)=101-e")V 电容电流为0=C普=e”A 7-11 图示电路中，开关S打开前己处于稳定状态。1-0开关S打开，求1之0时的4，)和电压源发出 的功率

则电流源发出的功率为 ) W 2 1 ( ) (1 2 2RC t S s P i u t Ri e  = =  7-10 图示电路中开关 S 闭合前，电容电压 C u 为零。在 t = 0 时 S 闭合，求 t>0 时的 u (t) C 和 i (t) C 。 解：由题意可知： uC (0+ ) = uC (0 ) = 0 ，这是一个求零状态的问题。在 t → 时电路 如题解 7-10 图所示。 由图可得 10 10 V 10 10 20 ( )  = + uC  = 等效电阻 R0 = (10//10) + 5=10 k 所以时间常数 s 10 1 10 10 10 10 3 6 = 0 =    =   R C 则 t > 0 时，电容电压 ( ) ( )(1 ) 10(1 ) V 10t t C C u t u e e   =   =   电容电流为 mA d d ( ) C 10t C e t u i t C  = = 7-11 图示电路中，开关 S 打开前已处于稳定状态。t = 0 开关 S 打开，求 t  0 时的 u (t) L 和电压源发出 的功率