《电路》课程教学资源（A）习题解答_第1章 电路模型和电路定律

第1章电路模型和电路定律 1-1 说明图(a),(b)中，(1)u,i的参考方向是否关联？(2)i乘积表示什么功率？(3)》 如果在图(a)中u>0,i0,元件实际发出还是吸收功率？ g元件9g元件9 题1-1图 06) 解：(1)当流过元件的电流的参考方向是从标示电压正极性的一端指向负极性的一 端，即电流的参考方向与元件两端电压降落的方向一致，称电压和电流的参考方向关联。 所以()图中4，i的参考方向是关联的：(b)图中4，i的参考方向为非关联。 (2)当取元件的u,i参考方向为关联参考方向时，定义p=m为元件吸收的功率： 当取元件的u,i参考方向为非关联时，定义p=i为元件发出的功率。所以(a)图中的 乘积表示元件吸收的功率(b)图中的乘积表示元件发出的功率。 (3)在电压、电流参考方向关联的条件下，带入u,i数值，经计算，若p=>0, 表示元件确实吸收了功率；若p0,i0,为正值， 表示元件确实发出功率：若0,i>0,有p=w>0,表示元件实际发出功率。 1-3 试校核图中电路所得解答是否满足功率平衡。（提示：求解电路以后，校核所得结果的 方法之一是核对电路中所有元件的功率平衡，即元件发出的总功率应等于其他元件吸收 的总功率)

第 1 章 电路模型和电路定律 1-1 说明图（a）,（b）中,（1） ui , 的参考方向是否关联？（2） ui 乘积表示什么功率？（3） 如果在图（a）中 u  0,i  0 ；图（b）中 u i   0, 0 ，元件实际发出还是吸收功率？ 解：（1）当流过元件的电流的参考方向是从标示电压正极性的一端指向负极性的一 端，即电流的参考方向与元件两端电压降落的方向一致，称电压和电流的参考方向关联。 所以（a）图中 u,i 的参考方向是关联的；（b）图中 u,i 的参考方向为非关联。 （2）当取元件的 u,i 参考方向为关联参考方向时，定义 p = ui 为元件吸收的功率； 当取元件的 u,i 参考方向为非关联时，定义 p = ui 为元件发出的功率。所以（a）图中的 ui 乘积表示元件吸收的功率；（b）图中的 ui 乘积表示元件发出的功率。 （3）在电压、电流参考方向关联的条件下，带入 u,i 数值，经计算，若 p = ui  0 ， 表示元件确实吸收了功率；若 p  0 ，表示元件吸收负功率，实际是发出功率。（a）图 中，若 u  0,i  0 ，则 p = ui  0 ，表示元件实际发出功率。 在 u,i 参考方向非关联的条件下，带入 u,i 数值，经计算，若 p = ui  0 ，为正值， 表示元件确实发出功率；若 p  0 ，为负值，表示元件发出负功率，实际是吸收功率。 所以（b）图中当 u  0,i  0 ，有 p = ui  0 ，表示元件实际发出功率。 1-3 试校核图中电路所得解答是否满足功率平衡。（提示：求解电路以后，校核所得结果的 方法之一是核对电路中所有元件的功率平衡，即元件发出的总功率应等于其他元件吸收 的总功率）

2A 题1-3园 解：由题1-3图可知，元件A的电压、电流为非关联参考方向，其余元件的电压电 流均为关联参考方向。所以各元件的功率分别为： P4=60×5=300W>0,为发出功率 P:=60×1=60W>0,为吸收功率 Pe=60×20=120W>0,为吸收功率 Po=40×2=80W>0,为吸收功率 PE=20×2=40W>0,为吸收功率 电路吸收的总功率 p=Pg+Po+Pe+Pg=60+120+80+40=300W 即，元件A发出的总功率等于其余元件吸收的总功率，满足功率平衡。 注：以上三题的解答说明，在电路中设电压、电流参考方向是非常必要的。在计算一段电路或 一个元件的功率时，如果不设电流、电压的参考方向，就无法判断该段电路或元件是发出还是吸收 功率。 此外还需指出：对一个完整的电路来说，它产生（或发出）的功率与吸收（或消耗）的功率总 是相等的，这称为功率平衡。功率平衡可以做为检验算得的电路中的电压、电流值是否正确的一个 判据。 1-4 在指定的电压u和电流i参考方向下，写出各元件“和1的约束方程（元件的组成关系）。 2

解：由题 1-3 图可知，元件 A 的电压、电流为非关联参考方向，其余元件的电压电 流均为关联参考方向。所以各元件的功率分别为： 60 5 300 0 A p W =  =  ，为发出功率 60 1 60 0 B p W =  =  ，为吸收功率 60 20 120 0 C p W =  =  ，为吸收功率 40 2 80 0 D p W =  =  ，为吸收功率 20 2 40 0 E p W =  =  ，为吸收功率 电路吸收的总功率 60 120 80 40 300 B D C E p p p p p W = + + + = + + + = 即，元件 A 发出的总功率等于其余元件吸收的总功率，满足功率平衡。 注：以上三题的解答说明，在电路中设电压、电流参考方向是非常必要的。在计算一段电路或 一个元件的功率时，如果不设电流、电压的参考方向，就无法判断该段电路或元件是发出还是吸收 功率。 此外还需指出：对一个完整的电路来说，它产生（或发出）的功率与吸收（或消耗）的功率总 是相等的，这称为功率平衡。功率平衡可以做为检验算得的电路中的电压、电流值是否正确的一个 判据。 1-4 在指定的电压 u 和电流 i 参考方向下，写出各元件 u 和 i 的约束方程（元件的组成关系）

解：()图为线性电阻，其电压、电流关系满足欧姆定律。需要明确的是：(1)欧姆定 律只适用于线性电阻：(2)如果电阻R上的电流、电压参考方向非关联，欧姆定律公式 中应冠以负号，即u)=一R()。由以上两点得()图电阻元件u和i的约束方程为 u=-Ri=-10×103i 欧姆定律表明，在参数值不等于零、不等于无限大的电阻上，电流与电压是同时存 在、同时消失的。即电阻是无记忆元件，也称即时元件。 （0)图为线性电感元作，其电压、电流关系的微分形式为：0=L加。如果电 压、电流参考方向为非关联，上式中应冠以负号，所以(b)图电感元件和1的约束方 程为 =-20x10帝 电感元件的电压、电流微分关系表明：(1)任何时刻，其电压与该时刻的电流变化 率成正比，显然直流时，电感电压为零，电感相当于短路。因此，电感是一个动态元件 (2)当电感上的电压为有限值时，电感中的电流不能跃变，应是时间的连续函数。 (⊙)图为线性电容元件，其电压、电流关系的微分形式为：0=C。如果电 医、电流的参考方向为非关联，上式中应冠以负号，即0=一C。所以(6)图电 容元件u和1的约束方程为 1=10x10*0=10-0 电容元件的电压。电流微分关系表明：(1)任何时刻，通过电容的电流与该时刻其 上的电压变化率成正比，即电容是一个动态元件。显然直流时，电容电流为零，电容相 当于开路。(2)当电容上的电流为有限值时，电容上的电压不能跃变，必须是时间的连 续函数。 ()图是理想电压源。理想电压源的特点为：(1)其端电压与流经它的电流方向、 大小无关。(2)其电压由它自身决定，与所接外电路无关，而流经它的电流由它及外电 路所共同决定。由以上特点得(d)图的约束方程为 =-5 ()图是理想电流源。理想电流源的特点为：(1)其发出的电流)与其两端电压 大小、方向无关。(2)其输出电流由它自身决定，与所接外电路无关，而它两端电压由

解：（a）图为线性电阻，其电压、电流关系满足欧姆定律。需要明确的是：（1）欧姆定 律只适用于线性电阻；（2）如果电阻 R 上的电流、电压参考方向非关联，欧姆定律公式 中应冠以负号，即 u(t) = −Ri(t) 。由以上两点得（a）图电阻元件 u 和 i 的约束方程为 u R i i 3 = − = −1010 欧姆定律表明，在参数值不等于零、不等于无限大的电阻上，电流与电压是同时存 在、同时消失的。即电阻是无记忆元件，也称即时元件。 （b）图为线性电感元件，其电压、电流关系的微分形式为： dt di t u t L ( ) ( ) = 。如果电 压、电流参考方向为非关联，上式中应冠以负号，所以（b）图电感元件 u 和 i 的约束方 程为 dt di u 3 20 10− = −  电感元件的电压、电流微分关系表明：（1）任何时刻，其电压与该时刻的电流变化 率成正比，显然直流时，电感电压为零，电感相当于短路。因此，电感是一个动态元件。 （2）当电感上的电压为有限值时，电感中的电流不能跃变，应是时间的连续函数。 （c）图为线性电容元件，其电压、电流关系的微分形式为： dt du t i t C ( ) ( ) = 。如果电 压、电流的参考方向为非关联，上式中应冠以负号，即 dt du t i t C ( ) ( ) = − 。所以（b）图电 容元件 u 和 i 的约束方程为 dt du dt du i 6 5 10 10 10 − − =  = 电容元件的电压。电流微分关系表明：（1）任何时刻，通过电容的电流与该时刻其 上的电压变化率成正比，即电容是一个动态元件。显然直流时，电容电流为零，电容相 当于开路。（2）当电容上的电流为有限值时，电容上的电压不能跃变，必须是时间的连 续函数。 （d）图是理想电压源。理想电压源的特点为：（1）其端电压与流经它的电流方向、 大小无关。（2）其电压由它自身决定，与所接外电路无关，而流经它的电流由它及外电 路所共同决定。由以上特点得（d）图的约束方程为 u = −5V （e）图是理想电流源。理想电流源的特点为：（1）其发出的电流 i(t) 与其两端电压 大小、方向无关。（2）其输出电流由它自身决定，与所接外电路无关，而它两端电压由

它输出的电流和外部电路共同决定。由以上特点得()图的约束方程为 1=2A 注：以上五个理想元件是电路分析中常遇到的元件。元件电压、电流的约束方程，反映了每 一元件的特性和确定的电磁性质。不论元件接入怎样的电路，其特性是不变的，即它的弘，约束方 程是不变的。因而深刻地理解和掌握这些方程，就是掌握元件的特性，对电路分析是非常重要的。 1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率（须说明是吸收还是发出）。 2A O 15V① 95215v 215v① 2A A (a) (b) (c) 题15图 解：(a)由欧姆定律和基尔霍夫电压定律可知各元件的电压、电流如解1-5图(a)故电 阻功率 P=i=10×2=20W(吸收20w) 电流源功率P=i=5×2=10W(吸收10W) 电压源功率发=M=15×2=30W(发出30W) (b)由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(b) 故电阻功率 P=12×3=45W(吸收45W) 电流源功率P饿=15×2=30W(发出30W) 电压源功率 发=15×1=15W(发出15W) (c)由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(c) 故电阻功率 P=15×3=45W(吸收45w) 电流源功率 P=15×2=30W(吸收30W) 电压源功率P=15×5=75W(发出75W) 1-8 试求图中各电路的电压U,并讨论其功率平衡

它输出的电流和外部电路共同决定。由以上特点得（e）图的约束方程为 i = 2 A 注：以上五个理想元件是电路分析中常遇到的元件。元件电压、电流的约束方程，反映了每 一元件的特性和确定的电磁性质。不论元件接入怎样的电路，其特性是不变的，即它的 ui , 约束方 程是不变的。因而深刻地理解和掌握这些方程，就是掌握元件的特性，对电路分析是非常重要的。 1-5 试求题 1-5 图中各电路中电压源、电流源及电阻的功率（须说明是吸收还是发出）。 15V + − 5 2A 15V + − 5 2A 15V + − 5 2A 15V + − 5 2A 15V + − 5 2A 15V + − 5 2A （a） （b） （c） 题 1-5 图 解：（a）由欧姆定律和基尔霍夫电压定律可知各元件的电压、电流如解 1-5 图（a）故 电 阻功率 P ui R吸 = =  = 10 2 20W （吸收 20W） 电流源功率 I P ui 吸 = =  = 5 2 10W （吸收 10W） 电压源功率 UP ui 发 = =  = 15 2 30W （发出 30W） （b）由基尔霍夫电压定律和电流定律可得各元件的电压电流如解 1-5 图（b） 故 电阻功率 PR吸 =  = 12 3 45W （吸收 45W） 电流源功率 I P发 =  = 15 2 30W （发出 30W） 电压源功率 UP 发 =  = 15 1 15W （发出 15W） （c）由基尔霍夫电压定律和电流定律可得各元件的电压电流如解 1-5 图（c） 故 电阻功率 PR吸 =  = 15 3 45W （吸收 45W） 电流源功率 I P吸 =  = 15 2 30W （吸收 30W） 电压源功率 UP 发 =  = 15 5 75W （发出 75W） 1-8 试求图中各电路的电压 U ，并讨论其功率平衡

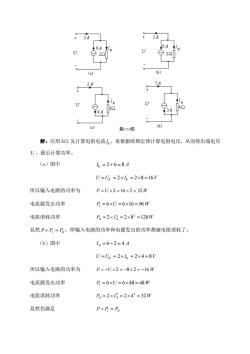
题1-13图 解：应用KCL先计算电阻电流！，再根据欧姆定律计算电阻电压，从而得出端电压 U,最后计算功率。 (a)图中 =2+6=8A U=U=2×1g=2×8=16V 所以输入电路的功率为 P=U×2=16×2=32W 电流源发出功率 P=6×U=6×16=96W 电阻消耗功率 P。=2×1R-2×82-128W 显然P+P=P。,即输入电路的功率和电源发出的功率都被电阻消耗了。 (b)图中 1R=6-2=4A U=Ug=2×1g=2×4=8V 所以输入电路的功率为 P=-U×2=-8×2=-16W 电流源发出功率 D=6×U=6×48=48W 电阻消耗功率 P。=2×1g=2×42=32W 显然仍满足 P+P=Pe

解：应用 KCL 先计算电阻电流 R I ，再根据欧姆定律计算电阻电压，从而得出端电压 U ，最后计算功率。 （a）图中 IR = 2 + 6 = 8 A U =UR = 2 IR = 28 =16V 所以输入电路的功率为 P = U  2 = 16 2 = 32 W 电流源发出功率 PI = 6U = 616 = 96W 电阻消耗功率 PR 2 I R 2 8 128W 2 2 =  =  = 显然 P + PI = PR ，即输入电路的功率和电源发出的功率都被电阻消耗了。 （b）图中 I R = 6 − 2 = 4 A U =UR = 2 IR = 24 = 8V 所以输入电路的功率为 P = −U  2 = −8 2 = −16 W 电流源发出功率 PI = 6U = 648 = 48W 电阻消耗功率 PR 2 I R 2 4 32W 2 2 =  =  = 显然仍满足 P + PI = PR

实际上电源发出的功率被电阻消耗了32甲，还有16W输送给了外电路。 (c)图中 1R=2-4=-2A U=UR=3×Ig=3×(-2)=-6V 所以输入电路的功率为 P=U×2=-6×2=-12W 电流源发出功率 D=4×6=24W 电阻消耗功率 P=3×I项=3×(-2)2=12W 即满足 P+P=P (d)图中 IR=5-3=2A U=Ug=4×1g=4×2=8V 各部分功率分别为 P=U×5-8×5=40W P=-3×U=-3×8=-24W P。=4×1R=4×22=16W 仍满足 P+P=Ps 1-10 电路如图所示，试求：(1)电流i,和u[图(a)]:(2)电压u[图(b)]。 450 52 209 +10v- +瑞1 、 42 09 0.05 要1-14图 解(a):受控电流源的电流为0.9%=i=0=2A 所以 4=09*2224 46=4×1ab=4×6-0.91)=4×0.1×20≈0.899p

实际上电源发出的功率被电阻消耗了 32 W ，还有 16W 输送给了外电路。 （c）图中 IR = 2 − 4 = −2 A U =UR = 3 IR = 3(−2) = −6V 所以输入电路的功率为 P = U  2 = −6 2 = −12 W 电流源发出功率 PI = 46 = 24W 电阻消耗功率 PR 3 I R 3 ( 2) 12W 2 2 =  =  − = 即满足 P + PI = PR （d）图中 I R = 5−3 = 2 A U =UR = 4 IR = 42 = 8V 各部分功率分别为 P = U 5 = 85 = 40 W PI = −3U = −38 = −24W PR 4 I R 4 2 16W 2 2 =  =  = 仍满足 P + PI = PR 1-10 电路如图所示，试求：（1）电流 1 i 和 ab u [图（a）]；（2）电压 cb u [图（b）]。 解（a）：受控电流源的电流为 i i 2 A 5 10 0.9 1 = = = 所以 i 2.222 A 0.9 2 1 =  ua b i a b i i 0.899V 9 20 = 4 = 4 ( 1 − 0.9 1 ) = 4 0.1 

解(b):因为4=2×5=10V,故受控电流源的电流为 i=0.054,=0.05×10=0.5A 而 ac=20×i=20×0.5=10V b=-3V 所以 4b=-4a+4a=-10-3=-13 1-12 对图示电路，若：(1)R,R2,R值不定；(2)R=R2=R。 在以上两种情况下，尽可能多的确定其他各电阻中的未知电流。 -10A 4 题1-16图 解：设定各电阻中未知电流的参考方向如图所示。 (1)若R,R,R值不定，4,2,3不能确定。对图中所示闭合面列KCL方程，根据 流进的电流等于流出的电流有 14=3+4-6=1A 对A点列KCL方程，可以解得 5=14+2-(-10)=1+2+10=13A (2)若R=R=R,对右边回路和B,C结点列KWL和KCL方程，有 TR4+R4+R43=0 4=3+, =+4 把方程组整理，代入R-R-R的条件，得

解（b）：因为 u1 = 25 =10V ，故受控电流源的电流为 i = 0.05u1 = 0.0510 = 0.5 A 而 uac = 20i = 200.5 =10V uab = −3V 所以 ucb = −uac + uab = −10 − 3 = −13V 1-12 对图示电路，若：（1） 1 2 3 R ,R ,R 值不定；（2） R1 = R2 = R3。 在以上两种情况下，尽可能多的确定其他各电阻中的未知电流。 解：设定各电阻中未知电流的参考方向如图所示。 （1）若 1 2 3 R ,R ,R 值不定， 1 2 3 i ,i ,i 不能确定。对图中所示闭合面列 KCL 方程，根据 流进的电流等于流出的电流有 i 4 = 3+ 4 − 6 =1 A 对 A 点列 KCL 方程，可以解得 i 5 = i 4 + 2 − (−10) =1+ 2 +10 =13 A （2）若 R1 = R2 = R3 ，对右边回路和 B，C 结点列 KVL 和 KCL 方程，有      = + = + + + = 4 3 0 2 3 1 2 1 1 2 2 3 3 i i i i R i R i R i 把方程组整理，代入 R1 = R2 = R3 的条件，得

i,+2+13=0 {1-12=3 2-13=4 应用行列式法解上面方程组 111 011 4=1-10=3△1=3-10=10 b1-1 41- 101 110 △2=130=1△，=1-13=-11 04-1 014 所以 4=会946-尝4,6=会=-号4 14,4的值同(1)。 1-13 图示电路中，已知42=2V,43=3V,4s=5V,4,=3V,46,=1V,尽可能多地确定其他 各元件的电压。 中中 白白。 题1-17图 解：已知4。=42=2V,44=42=3V,4。=42s=5V,4,=6=1V,选取回路列KWL 方程。 对回路（①②⑤①）有4。=45=42+425 所以 4。=2+5=7p 对回路（①②③①）有

     − = − = + + = 4 3 0 2 3 1 2 1 2 3 i i i i i i i 应用行列式法解上面方程组 10 4 1 1 3 1 0 0 1 1 3 0 1 1 1 1 0 1 1 1 1 = − =  = − −  = − 11 0 1 4 1 1 3 1 1 0 1 0 4 1 1 3 0 1 0 1 2 = 3 = − = − −  = 所以 i A i A i A 3 11 , 3 1 , 3 10 3 3 2 2 1 1 = −   = =   = =   = 4 5 i i , 的值同（1）。 1-13 图示电路中，已知 u12 = 2V,u23 = 3V,u25 = 5V,u37 = 3V,u67 =1V ，尽可能多地确定其他 各元件的电压。 解：已知 ub = u12 = 2V,ud = u23 = 3V,uc = u25 = 5V,u j = u67 = 1V ，选取回路列 KVL 方程。 对回路（①②⑤①）有 ua = u15 = u12 + u25 所以 ua = 2 + 5 = 7V 对回路（①②③①）有

M=43=42+423=2+3=5V 对回路（②③④⑦⑥⑤②）有 ,+4gn-46,-h6-4s=0 所以 4y=us6=423+u37-67-山2s =3+3-1-5=0V 对回路（③④⑦⑥③）有 4。=46=4)-467=3-1=2V 对回路（⑤⑥⑦⑤）有 4=4,=6+4o,=0+1=1V 1-14 对上题所示电路，指定个支路电流的参考方向，然后列出所有结点处的KCL方程，并说 明这些方程中有几个是独立的。 解：支路电流的参考方向如图所示，各结点的KCL方程分别为（以流出结点的电流 为正) ①1，+1+1=0 ②-1+1.+i4=0 ③-i+i。+人-1=0 ⑤-1-1。+4+4=0 ⑥-1.-i+i=0 ⑦-1，-1-1。=0 把以上6个方程相加，得到0=0的结果。说明6个方程不是相互独立的，但是其 中任意5个方程是相互独立的： 注：一个有n个结点的电路，依CL列结点电流方程，则n-1个方程将是相互独立的。这是 因为任一条支路一定与电路中两个结点相连，它上面的电流必定从其中一个结点流出，又流入另一 个结点，因此，在个CL方程中，每个支路电流一定出现2次，一次为正，另一次为负，若把m 个方程相加，必定得到等于零的恒等式。即n个KCL方程不是相互独立的，但从n个方程中任意去 掉一个结点电流方程，余下的-1个方程是相互独立的。 1-15 电路如图所示，按指定的电流参考方向列出所有可能的回路的KWL方程。这些方程都独

uk = u13 = u12 + u23 = 2 + 3 = 5V 对回路（②③④⑦⑥⑤②）有 u23 + u37 − u67 − u56 − u25 = 0 所以 V u f u u u u u 3 3 1 5 0 56 23 37 67 25 = + − − = = = + − − 对回路（③④⑦⑥③）有 ue = u36 = u37 − u67 = 3−1 = 2V 对回路（⑤⑥⑦⑤）有 ui = u57 = u56 + u67 = 0 +1 =1V 1-14 对上题所示电路，指定个支路电流的参考方向，然后列出所有结点处的 KCL 方程，并说 明这些方程中有几个是独立的。 解：支路电流的参考方向如图所示，各结点的 KCL 方程分别为（以流出结点的电流 为正） ① i a + i b + i k = 0 ②− i b + i c + i d = 0 ③ − i d + i g + i e − i k = 0 ⑤− i a − i c + i f + i i = 0 ⑥ − i e − i f + i j = 0 ⑦− i j − i i − i g = 0 把以上 6 个方程相加，得到 0 = 0 的结果。说明 6 个方程不是相互独立的，但是其 中任意 5 个方程是相互独立的。 注：一个有 n 个结点的电路，依 KCL 列结点电流方程，则 n-1 个方程将是相互独立的。这是 因为任一条支路一定与电路中两个结点相连，它上面的电流必定从其中一个结点流出，又流入另一 个结点，因此，在 n 个 KCL 方程中，每个支路电流一定出现 2 次，一次为正，另一次为负，若把 n 个方程相加，必定得到等于零的恒等式。即 n 个 KCL 方程不是相互独立的，但从 n 个方程中任意去 掉一个结点电流方程，余下的 n-1 个方程是相互独立的。 1-15 电路如图所示，按指定的电流参考方向列出所有可能的回路的 KVL 方程。这些方程都独

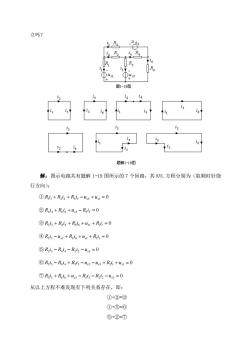
立吗？ R 题1-19图 题解1-19图 解：图示电路共有题解1-19图所示的7个回路，其KVL方程分别为（取顺时针绕 行方向： ①R4+R42+R45-s+41=0 ②R,+R。+us-R,=0 ③R2+R4+R6+41+R4=0 ④R,3-43+R,。+u1+R4=0 ⑤R4,-R44-R42-43=0 ⑥R-R4+R4-4s-u+R4+1=0 ⑦R3+R。+u5-R5-R42-43=0 从以上方程不难发现有下列关系存在，即： ①+②=③ ①+⑤=⑥ ⑤+②-⑦

立吗？ 解：图示电路共有题解 1-19 图所示的 7 个回路，其 KVL 方程分别为（取顺时针绕 行方向）： ① R1 i 1 + R2 i 2 + R5 i 5 − us5 + us1 = 0 ② R4 i 4 + R6 i 6 + us5 − R5 i 5 = 0 ③ R2 i 2 + R4 i 4 + R6 i 6 + us1 + R1 i 1 = 0 ④ R3 i 3 − us3 + R6 i 6 + us1 + R1 i 1 = 0 ⑤ R3 i 3 − R4 i 4 − R2 i 2 − us3 = 0 ⑥ R3 i 3 − R4 i 4 + R5 i 5 − us5 − us3 + R1 i 1 + us1 = 0 ⑦ R3 i 3 + R6 i 6 + us5 − R5 i 5 − R2 i 2 − us3 = 0 从以上方程不难发现有下列关系存在，即： ①+②=③ ①+⑤=⑥ ⑤+②=⑦