《电路》课程教学资源（A）习题解答_第9章 正弦稳态电路的分析

第9章正弦稳态电路的分析 9-1 试求图示各电路的输入阻抗Z和导纳Y。 照o22仁子1-2n 2-1 1.11+21=02+j04S 21-25 2左1+-x0+》-1+0-0=2-jQ -j+1+) 1=2+1=04+025 o食oc+上tc+s R+ joC joc=- R-1 1)2 R+jeC+JROC+1+0CR-OCR) 12 12 22 -12 12 (a)

第 9 章 正弦稳态电路的分析 9-1 试求图示各电路的输入阻抗 Z 和导纳 Y。 解：（a）Z=1+ ( ) 2 1 2 1 j j j j −  − =1+ j 2 =1− 2 j  Y= Z 1 = 1 2 j 1 − = 5 1+ 2 j = 0.2 + j0.4 S Z= (1 ) (1 ) 1 j j j j − + + −  + + =1+ (1− j) = 2 − j  Y= j S j Z j 0.4 0.2 5 2 2 1 1 = + + = − = （c） Y= 1 1 1 1 + = + + + + + Rj C j C j C R j C R j C R I      S Z=       + − − = + + + = CR j CR C R j jR C j C j C R Y       1 3 1 1 1 1 1 

402 4021 403 -j402 (d) + ④-ri /wC (e) 题91图 40-j40+40+j40 闭r=40+0+0-m0+040-00=0255 Z-=400 (e)设端口电压相量为0，根据KVL,得 U=joLi-ri=(joL-r)i 所以输入阻抗为 z9-a 8了立成，5 f)）设端口电压，电流相量为U,i,根据KCL,得 i=-m2-i2=-0+B)i3 且有 所以输入阻抗

题 9-1 图 (d) ( )( ) S j j j j j j Y 0.025 40 1 40 40 40 40 40 40 40 40 40 40 1 40 40 1 = = + − − + + = − + + = = = 40 1 Y Z (e) 设端口电压相量为 U  ，根据 KVL，得 U j LI rI (j L r)I  =   −  =  −  所以输入阻抗为 = = j L − r I U Z    导纳 ( ) S r l j L r Z j L r Y 2 2 1 1    + − − = − = = (f ) 设端口电压，电流相量为 U  ， I  ，根据 KCL，得 ( ) 2 2 1 2 I I I I  = −  −  = − +   且有 2 1 I j C U   = − 所以输入阻抗

1 导纳 y-Jcs 注：本题的求解过程说明，引入阻抗和导纳的概念以后，正弦电路的输入阻抗（或导纳）的定义与 计算和直流电路输入电阻（或电导）的定义与计算是相似的。即输入阻抗 若有n个阻抗串联，等效阻抗Z=∑乙.=2(R+X,) 若有n个导纳并联，等效导纳为Y=y:=立G,+B,) 只不过Z和Y是复数。 9-2 已知国示电路中=50sn1or+},=40eoo+君引A.试求电路中合适的元#值（等效。 解：把u用余弦函数表示有 u=50co10-} u和I的相量形式为 0=50 -45r.i=400∠30A 根据入端导纳的定义，有 .i-4001W2∠30 y=元50122-45 =8∠75°=2.07+7.73S 既图示的两并联元件为电导和电容，其参数为 G=2.07S c=773-73=073F 0 10 注：以上计算表明，导纳的模等于电流广与电压心的模值之比，导纳角等于电流广与电压的相位 差，若导纳角,>0,表示电流超前电压0，导纳为电容性，反之为电感性

( ) ( )  + = − − + − = =     1 1 1 C j C j I U Z   导纳 j C( )S Z Y = =  1+  1 注：本题的求解过程说明，引入阻抗和导纳的概念以后，正弦电路的输入阻抗（或导纳）的定义与 计算和直流电路输入电阻（或电导）的定义与计算是相似的。即输入阻抗 I Y U Z 1 = =   若有 n 个阻抗串联，等效阻抗  ( ) = = = = + n k k k n k k Z Z R jX 1 1 若有 n 个导纳并联，等效导纳为  ( ) = = = = + n k k k n k K Y Y G jB 1 1 只不过Ｚ和Ｙ是复数。 9-2 已知图示电路中 u t V      = + 4 50sin 10  ，i t A      = + 6 400cos 10  。试求电路中合适的元件值（等效）。 解：把 u 用余弦函数表示有 u t V      = − 4 50cos 10  u 和 I 的相量形式为 U V  =  − 45 2 50  , I A  = 30 2 400  根据入端导纳的定义，有 j S U I Y 8 75 2.07 7.73 50 / 2 45 400 / 2 30 =  = +  −  = =      既图示的两并联元件为电导和电容，其参数为 G = 2.07S C 0.773F 10 7.73 7.73 = = =  注：以上计算表明，导纳的模等于电流 I  与电压 U  的模值之比，导纳角等于电流 I  与电压 U  的相位 差，若导纳角   0 y ，表示电流 I  超前电压 U  ，导纳为电容性，反之为电感性

题9-2 9-3 附图中N为不含独立源的一端口，端口电压u,电流I分别如下列各式所示。试求没一种情况下的 输入阻抗乙和导纳Y,并给出等效电路图（包括元件的参数值）。 (1) u=200cos314)W i=10cos(314)A: (2) u=10cos(101+45)W i=2cos(101-90)4 (3) u=100cos(21+60')Ψ i-5cos(21-30)A [u=40cos(100r+17)V (4) =8sm100+74 解：(1)u和i的相量为 0.20∠0y i804 意93国 即等效电路 为202的电阻，如题解图(a)所示

9-3 附图中 N 为不含独立源的一端口，端口电压 u，电流 I 分别如下列各式所示。试求没一种情况下的 输入阻抗 Z 和导纳 Y，并给出等效电路图（包括元件的参数值）。 （1）    = = i t A u t V 10cos(314 ) 200cos(314 ) ； （2）     = − = +   i t A u t V 2cos(10 90 ) 10cos(10 45 ) ； （3）     = − = +   i t A u t V 5cos(2 30 ) 100cos(2 60 ) ； （4）      = + = +  i t A u t V ) 2 8sin(100 40cos(100 17 )  。 解：（1）u 和 i 的相量为 U V  = 0 2 200  I A  = 0 2 10  根据输入阻抗的定义有 = = 20 10 200 I U Z   S Z Y 0.05 20 1 1 = = = 即等效电路 为 20  的电阻，如题解图（a）所示

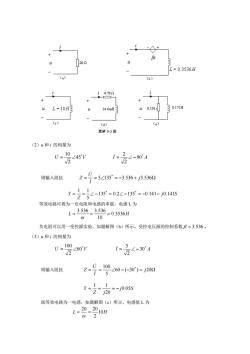
L=0.3536H a) () 4.80 4L=10H 0.191 .171 (e) 解93 (2)M和1的相量为 <45 0=10 <904 2 i=- 则输入阻抗 z-9-5435-3536+B536n y=-13s=02-135=-0141-014s 等效电路可视为一负电阻和电感的串联，电感L为 L=3536_3.536=03536H 10 负电阻可以用一受控源实验，如题解图(b)所示。受控电压源的控制系数B-3.536。 (3)u和1的相量为 0-罗4r 1=店4-04 则输入阻抗 z-号-940-30-2m -艺高0s 既等效电路为一电感，如题解图（©）所示，电感值L为

（2）u 和 i 的相量为 U V  = 45 2 10  I A  =  − 90 2 2  则输入阻抗 = =  = − +   5 135 3.536 j3.536 I U Z   j S Z Y 135 0.2 135 0.141 0.141 5 1 1 = =  − =  − = − −   等效电路可视为一负电阻和电感的串联，电感 L 为 L 0.3536H 10 3.536 3.536 = = =  负电阻可以用一受控源实验，如题解图（b）所示。受控电压源的控制系数  = 3.536 。 （3）u 和 i 的相量为 U  V  = 60 2 100 I A  =  − 30 2 5  则输入阻抗 I U Z   = =  − − =   60 ( 30 ) 20 5 100 j j S Z j Y 0.05 20 1 1 = = = − 既等效电路为一电感，如题解图（c）所示，电感值 L 为 L 10H 2 20 20 = = 

(4)M和1的相量为 则验入鼠抗乙-号智A7=5☑T=48+刀@ 1 Y=z547 =0.2∠-17=0.191-j0.0585S 既等效电路为一个478Q的电阻和一电感串联，电感值L为 1=1塔胎-146mn 电路如题解图(d)所示。也可以用一个0191S的电导和一电感并联等效，如题解图()所示。 电感值为 1 L=0x0.0585100x0.0585=0.171H 94 求附图(a),(b)中的电压U,并画出电路的相量图。 解：(a)电路的总导纳为 (b)根据KV可得0=(U20-j25)×2∠0°=-j10/ 图(a)和(b)对应的相量图如题解9-4图(a)和(b)所示。 2∠0A 42 + + -j25 152 3j19 -j12 i, -2∠0A (a) 意94

（4）u 和 i 的相量为 U V  = 17 2 40  I A  = 0 2 8  则输入阻抗 I U Z   = =  =  = +    17 5 17 4.78 1.46 8 40 j j S Z Y 0.2 17 0.191 0.0585 5 17 1 1 =  − = −  = =   既等效电路为一个 4.78  的电阻和一电感串联，电感值 L 为 L 14.6mH 100 1.46 1.46 = = =  电路如题解图（d）所示。也可以用一个 0.191S 的电导和一电感并联等效，如题解图（e）所示。 电感值为 L 0.171H 100 0.0585 1 0.0585 1 =  =  =  9-4 求附图（a），（b）中的电压 . U ，并画出电路的相量图。 解：（a）电路的总导纳为 S j j Y 0.2 5 1 1 1 1 1 5 1 = + − = = 故电压 V Y I U 10 0.2 2 0 =  = =    （b）根据 KVL 可得 U = ( j20 − j25) 20 = − j10V   图（a）和（b）对应的相量图如题解 9-4 图（a）和（b）所示

Us （a) 意解94 (6) 9-5 已知图示电路中i=2∠0°A,求电压0，并作电路的相量图。 32 142m 0: 0, -j53 Ux Ue-U 意95图 Us U 意邮95田 解：电路的总阻抗为 Z-4+j3-j5=4-j20 所以电压0.==2∠0°×(4-j2)=8-j4=8.94∠-26.565 各元件的电压为 0R=4×2∠0°=8 0:=j3×2∠0°=j6 0e=-j5×2∠0°=-j10v 相量图如愿解95图所示。 9-6 附图电路中，1，=10AU,-10,求电流广和电压心，并画出电路的相量图。 √2 解：设i2为参考相量，既2=10∠0°A,则b两端的电压相量为 0b=-j1×i2=-jl×10=-j10

9-5 已知图示电路中 I 2 0 A,   =  求电压 U S  ，并作电路的相量图。 解：电路的总阻抗为 Z = 4 + j3 − j5 = 4 − j2 所以电压 Us IZ j j V   = = 20  (4 − 2) = 8 − 4 = 8.94 − 26.565   各元件的电压为 UR = 4 20 = 8V   UL = j3 20 = j6V   UC = − j5 20 = − j10V   相量图如题解 9-5 图所示。 9-6 附图电路中， , 2 10 10 , I 2 = A Us = V 求电流 I  和电压 U S  ，并画出电路的相量图。 解：设 2 I  为参考相量，既 2 I  A  = 100 ，则 ab 两端的电压相量为 U  ab = − j1 I  2 = − j110 = − j10V

电-华-n04 i=i+i2=-10+10=10W2∠-45A 由KVL,得 U,=Xz1+Ub=X2×10W2∠-45-10 =j10X,0-)-10=j10(X2-1)+10X: 因为0：的有效值为发所以有红等式 (得-e-明+0oxy 低X2X+好0 从中解得X,= 2 故Us相量为 0.=x,1+U=j分×102∠-45-10 =5-j5=万1 相量图如题解96图所示。 i i2 0s白 121 卡-j12 意解9-6图 意96厨 7 附图中已知u,=2002c0sB14+π/3)V,电流表的读数为24，电压表V,V,的读数均为200V。 求参数R,L,C,并做出该电路的相量图（提示：可先做相量图辅助计算）。 解法一：利用相量图求解。 因为电压山，'2的有效值均为200V,因此，构成的电压三角形为等边三角形ABC如题

电流 j A U I ab 10 1 1 = = −   I I I j A  = 1 + 2 = − 10 +10 = 10 2 − 45    由 KVL，得 10 2 45 10 . . . U jX I U jX j L ab L s = + =   − −  = L XL XL j10X (1− j) − j10 = j10( −1) +10 因为 U S . 的有效值为 2 10 ，所以有恒等式  ( ) ( ) 2 2 2 10 1 10 2 10 = XL − + XL       既 0 4 2 1 X L − X L + = 从中解得 =   −  = 2 1 2 4 1 1 1 4 X L 故 U S . 相量为 10 2 45 10 2 1 . . . U jX I U j j L a b s = + =   − −  j V  = − =  − 45 2 10 5 5 相量图如题解 9-6 图所示。 9-7 附图中已知 u s =200 2 cos (314t + /3) V ，电流表的读数为 2A，电压表 V 1 ，V 2 的读数均为 200V。 求参数 R，L，C，并做出该电路的相量图（提示：可先做相量图辅助计算）。 解法一：利用相量图求解。 因为电压 s u ，V1 ，V2 的有效值均为 200V，因此，构成的电压三角形为等边三角形 ABC 如题

解图所示。由题意知电压Us相量为三角形的AB边，若V,相量为CA边，则根据电容元件的电压， 电流关系得电流1相量超前'290°，那么ì与0s的相位差为150°，电源发出的功率 P=U,Icos150'为负值。这是不合理的，由此可得V2相量应该是三角形的BC边，V1相量为CA 边，电流1相量超前U,30°，如愿解9-7图所示。各相量为 Us=200∠60V V1=200∠120V ∥2=200∠0^y 1=2∠90°A 故根据欧姆定律的相量形式，有 -X.=.20020-1000 2 1 1 C=aK.314x100=31.85m R+X,=上-20020-1000n 2∠90° R=100cos30°=86.62 L-X-100sn30-0.159H 314 解法二：根据电压电流有效值关系，可得 2 1 1 C=ox10034x10-3185uf us 1卡 301 Us 60 意97田 意9-7厨 Z=R+x-当-0=10m 2

解图所示。由题意知电压 U S . 相量为三角形的 AB 边，若 V2 相量为 CA 边，则根据电容元件的电压， 电 流 关系 得 电流 . I 相量超前 V2  90 ，那么 . I 与 U S . 的 相 位 差为  150 ， 电 源 发出 的 功 率 P=  Us I cos150 为负值。这是不合理的，由此可得 2 . V 相量应该是三角形的 BC 边， 1 . V 相量为 CA 边，电流 . I 相量超前  30 . U s ，如题解 9-7 图所示。各相量为 U S . =2 V  0060 1 . V =200 V  120 2 . V =200 V  0 . I =2 A  90 故根据欧姆定律的相量形式，有 = −   − = =  100 2 200 0 . . 2 j j I V jXc F X C c   31.85 314 100 1 1 =  = = =     + = =    100 30 2 90 200 120 . . 1 I V R jXL 即 = =   R 100cos30 86.6 H X L L 0.159 314 100sin 30 = = =   解法二：根据电压电流有效值关系，可得 = = = =100 2 1 2 200 I V C Xc  C F  31.85 314 100 1 100 1 =  =  = = + = = =100 2 1 200 I V Z R jXL

Z的阻抗角为广1和7相量间的相位差，为简便计算，设1=2∠0°A,∥1=200∠@，V ，Us=200∠p,V2=-j200r 由KVL得 200∠0，=200∠g,-j200 即 sin o,=sin -1 把以上两式平方后相加，解得 9=30 故有 Z=上.200∠30=100∠30=866+/50n Γ2∠0° 所以R=86.62 -9-品-oi5m 显然本题用相量图解既直观又简便。 9-8 附图中i,=14、2cos(cm+p)mA,调节电容，使电压U=U∠p,电流表A,的读数为50mA。求电 流表A,的读数。 I. 惠9-8国 惠解9-8图 解法一：根据相量图计算。 设p=0°，则各电压，电流相量为 1,=14∠0°A, U=U∠0V 1为电感性支路的电流，12为电容性支路的电流，所以，1滞后0一角度？，12超前090 画相量图如题解9-8图所示。山，1：，1：构成一直角三角形。故电流表4：的读数为 12=V-1=V502-142=48mA

Z 的阻抗角为 1 . V 和 . I 相量间的相位差，为简便计算，设 . I =2 A  0 ， 1 . V = 2001V ，U S . = 200 s ， 2 . V = − j200V 由 KVL 得 200 s = 2001 − j200 即 1 cos s = cos sin  s = sin 1 −1 把以上两式平方后相加，解得 2 1 sin 1 =  1 = 30 故有 =  = +    = =    100 30 86.6 50 2 0 200 30 . . 1 j I V Z 所以 R = 86.6 L 0.159H 314 50 50 = = =  显然本题用相量图解既直观又简便。 9-8 附图中 i s =14 2 cos(t +)mA ，调节电容，使电压 . U =U ，电流表 A1 的读数为 50 mA 。求电 流表 A2 的读数。 解法一：根据相量图计算。 设   = 0 ，则各电压，电流相量为 I s A  = 140 . ， U U V  = 0 . 1 . I 为电感性支路的电流， 2 . I 为电容性支路的电流，所以， 1 . I 滞后 . U 一角度 1 ， 2 . I 超前 . U  90 。 画相量图如题解 9-8 图所示。 1 . I ， 2 . I ， I s . 构成一直角三角形。故电流表 A2 的读数为 I I Is 50 14 48mA 2 2 2 2 2 = 1 − = − =